Вытекание жидкости через отверстия и насадки

1. Вытекание жидкости через отверстие в тонкой стенке

Рассмотрим случай вытекания жидкости в атмосферу через отверстие площадью ω (рис.45).

Рис.45.

Струя при вытекании через отверстие постепенно сжи­мается. Ближайшее к отверстию наименьшее живое сечение С-С, в котором движе­ние можно рассматривать плавноизменяющимся, называется сжатым сечением. Обо­значим площадь сжатого сече­ния С-С буквой ω_сж. Отноше­ние

(91)

называется коэффициентом сжа­тия.

Так как отдельные струйки в сжатом сечении почти параллельны, то можно считать, что давление в нем равно давлению окружающей среды, т. е. в данном случае барометрическому давлению р_б.

Обозначим Н высоту уровня жидкости над центром тяжести отверстия, v -скорость в сжатом сечении. Выберем за ось координат горизонтальную ось X-X, проходящую через центр тяжести отверстия, и напишем уравнение Бернулли для сечения О-О и сжатого сече­ния С-С:

,

где v₀ – скорость воды в сосуде.

Пренебрегая величиной (v₀²/2g) (ввиду ее малости по сравнению с Н), получим

,

откуда скорость вытекания

(92)

где называют коэффициентом скорости. Коэффициент скорости является отношением скоростей реальной и идеальной жидкости при вытекании через отверстия и насадки.

Для вычисления расхода жидкости через отверстие надо скорость умножить на площадь сжатого сечения:

Учитывая, что

(93)

Обозначим

(94)

Величина μ называется коэффициентом расхода (отношение расхода реальной жидкости через отверстие к расходу идеальной жидкости при вытекании через отверстия и насадки). Выражение (94) является безразмерной формой для уравнения неразрывности потока, а (93) принимает вид

(95)

2. Вытекание жидкости через затопленное отверстие

Рассмотрим вытекание жидкости через затопленное отверстие (рис.46). Обозначим v скорость в сжатом сечении С-С, а Н- разность уровней в баках I и II.

Приняв за плоскость сравнения плоскость X-X, запишем уравнение Бернулли для сечений О-О и С-С

Рис.46.

В этом уравнении можно принять равным нулю, а

Поэтому

или

(96)

где

Соответственно

(97)

или

(98)

Исследованиями установлено, что коэффициент расхода μ для затопленного отверстия можно принимать равным коэффициенту μ при вытека­нии в атмосферу.

3. Классификация отверстий и насадок

На рис.47,а изображен сосуд, имеющий в одной из своих стенок отверстие. Обозначим толщину стенки сосуда L , а диаметр отверстия D. Если L< 3D, то стенку рассматривают как тонкую и отверстие называют отверстием в тонкой стенке. При вытекании жидкости через такое отверстие все потери напора сведутся к местным потерям. При L=3÷5D отверстие рассматривается, как короткая трубка, вставленная в отверстие или насадок (рис.47,б).

а) б)

Рис.47.

а) б)

Рис.48.

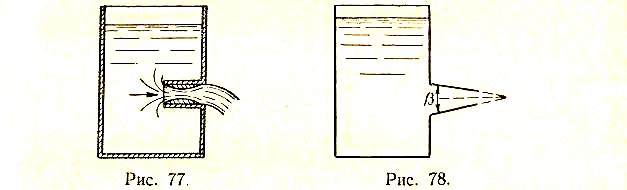
Насадки разделяются на цилиндрические и конические. Цилиндрические насадки могут быть внешние (рис.47,б) и внутренние (рис48,а). Конические насадки бывают конически сходящиеся (рис.48,б) и конически расходящиеся (рис.49 и 50), причем угол β между образующими конуса называется углом конусности. Если в конически расходя­щейся насадке (β>0,04π) то, как показывают опыты, струя вытекает из отверстия, не касаясь стенок насадки (рис.50).

Рис.49.

Рис.50.