5. Принцип Вентури

Пусть имеется горизонтальная, труба переменного диа­метра (рис. 28). Обозначим площади живых сечений 1 и 2 трубы соответственно ω₁ и ω₂ (причем ω₁ > ω₂), сред­ние скорости – v₁ и v₂ , давления - р₁ и р₂. Координаты центров тяжести этих сечений - z₁ и z₂ (причем z₁ = z₂).

Рис.28

Применим к сечениям 1 и 2 уравнение неразрывности (35) и уравнение энергии (43). Тогда

(потерями энергии h_1-2 на участке 1-2 для простоты рассуждений пренебрегаем) или

(45)

На основании уравнения неразрыв­ности, если ω₁ > ω₂, получим v₁ < v₂ , a следовательно, и v²₁/2g< v²₂/2g. Но тогда из уравне­ния (45) следует, что р₁>р₂. При уменьшении площади живого сечения давление уменьшается, а при увеличении увеличивается. Высказанное положение называется принципом Вентури.

6. Классификация потерь напора

Потери напора делятся на два вида: потери напора по длине и местные потери напора.

Потерями напора по длине называются потери удельной энергии на преодоление сопротивлений на участках потока с равномерным движением. Потери напора по длине обозначаются буквой h с индексом, определяющим границы участка.

Местными потерями напора называются потери удельной энергии на преодоление сопротивлений на участках потока с нарушенной равномерностью дви­жения.

ГЛАВА ШЕСТАЯ

Потери напора по длине

1. Основное уравнение равномерного движения

Рассмотрим прямолинейное равномерное движение жидкости. Живые сечения в этом случае могут быть про­извольной формы, но не должны изменяться по всей длине рассматриваемого участка. В таком потоке потеря напора определяется лишь потерей по длине.

Выделим из потока участок жидкости (рис. 29) длиной L и напишем уравнение Бернулли для сечений 1 и 2.

(46)

где z₁ , z₂ - ординаты центра тяжести сечений 1 и 2; p₁ и р₂ - давления в центрах тяжести этих сечений; v₁ и v₂ - средние скорости в этих сечениях;

h_1-2 - потеря напора по длине.

Рис.29

Так как движение равномерное, то v₁ = v₂ и уравне­ние (46) можно переписать так:

(47)

т.е. в случае равномерного движения разность удельных потенциальных энергий равна потере напора по длине. Для вычисления этой разности напишем сумму проек­ций на ось потока А-А всех сил, действующих на участке 1-2. Эта сумма должна равняться нулю, так как при равномерном движении все силы уравновешиваются. Эти силы следующие:

1. сила тяжести жидкости 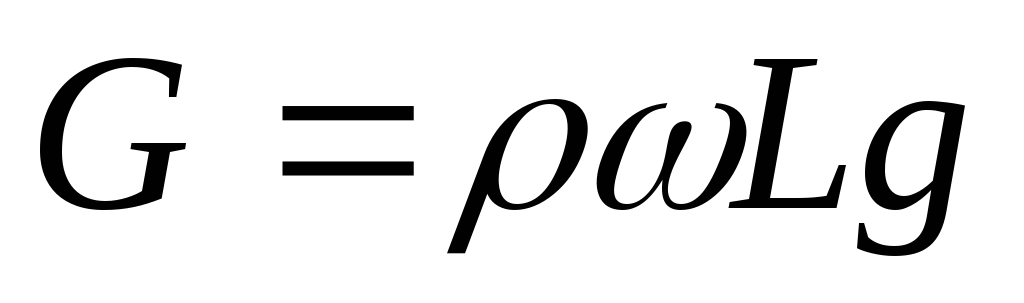, где ω=ω₁= ω₂ - площади живых сечений;

2. силы давления на плоские сечения ω₁ и ω₂, равные Р₁= р₁ω₁ и Р₂ = р₂ω₂;

1. силы давления на боковую поверхность;

3. сила трения ; где τ – сила трения на единицу площади боковой поверхности цилиндра, а χ - смоченный периметр.

Спроектируем все эти силы на ось А-А:

(48)

Из рисунка 29 видно . Подставив значения сил в (48), получим

Разделим обе части этого равенства на ρωLg:

(49)

Откуда

(50)

Имея в виду, что (ω/χ)= R, a ( h_1-2/L)= i, из уравне­ния (50) получим

(51)

Уравнение (51) называется основным уравнением рав­номерного движения.

Величина gRi имеет размерность квадрата скорости. Величина называется динамической ско­ростью и для краткости обозначается , т. е.

(52)