
- •1 Комплексная плоскость
- •1.1 Комплексные числа
- •Задачи
- •1.2 Области, пути и кривые,
- •2 Функции комплексного переменного
- •2.1 Понятие функции
- •2.2 Предел функции
- •2.3 Непрерывность
- •2.4 Линейные функции
- •2.5 Дифференцируемость
- •2.6 Геометрическая интерпретация производной
- •3 Стереографическая проекция
- •3.1 Стереографическая проекция и бесконечность
- •3.2 Свойства стереографической проекции
- •3.2.1 Сохранение углов
- •3.2.2 Круговое свойство
3Стереографическая проекция
3.1Стереографическая проекция и бесконечность
Многие свойства комплексных чисел проще и нагляднее описываются с помощью так называемой стереографической проекции. Представим комплексную плоскость в трёхмерном пространстве. Выберем в пространстве декартову систему координат так, чтобы действительная ось совпадала с осью абсцисс, мнимая — с осью ординат, и построим сферу S радиуса 1 с центром в начале координат, см. рис.1.
О п р е д е л е н и е 1. Сфера S называется сферой Римана.
Будем пользоваться географической терминологией: окружность, которая является пересечением комплексной плоскости с S , называется экватором, верхняя полусфера — северной, нижняя — южной, пересечения с вертикальной осью — полюсами (северным и южным). Угол ψ , см. рис.1, между радиус-вектором точки сферы и экваториальной
плоскостью называется широтой и изменяется от −π |
(южный полюс) до |
π |
(северный |
2 |
|
2 |
|
полюс) включительно. Угол φ между положительным направлением действительной оси и проекцией радиус-вектора точки сферы на экваториальную плоскость, отсчитываемый против часовой стрелки, называется долготой и изменяется от 0 (включительно) до 2 π (не включая 2 π ).
Линия {ψ =const , 0 φ<2 π} называется параллелью, линия {φ=const , −π/2<ψ <π/2 } - меридианом.
На рис.1 северный полюс обозначен через N.
Каждой точке A сферы Римана сопоставим точку A' пересечения луча NA с плоскостью , см. рис.1. Это отображение и называется стереографической проекцией. Очевидно, что каждой точке сферы Римана, за исключением N, сопоставляется одна точка
, и наоборот, каждой точке сопоставлена ровно одна точка S.
57
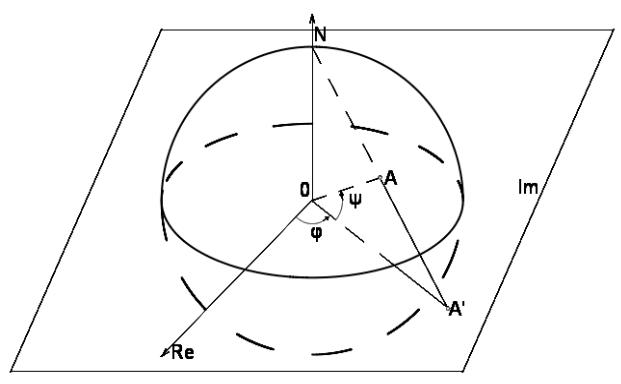
Рис. 1. |
|
|
|
|
|
|
|
|
|
|
|||||
З а д а ч а 1. Пусть |
ξ , η , ζ |
- координаты точки A. Найти координаты x , y точки A' . |
|||||||||||||
Р е ш е н и е. Из подобия прямоугольных треугольников A'CO и BDO, см. рис.2, следует |
|||||||||||||||
|
x |
= |
y |
= A' O |
. Из подобия прямоугольных треугольников A'NO и ANE следует |
||||||||||
|
ξ |
|
|
||||||||||||
|
|
η |
BO |
|
|
|
|
|
|
|
|
||||
|
A' O |
= |
1 |
|
. Но |
AE= BO |
, поэтому, |
x= |
ξ |
, y= |
η |
.■ |
|||
|
|
1−ζ |
1−ζ |
1−ζ |
|||||||||||
|
AE |
|
|
|
|
|
|
||||||||
58
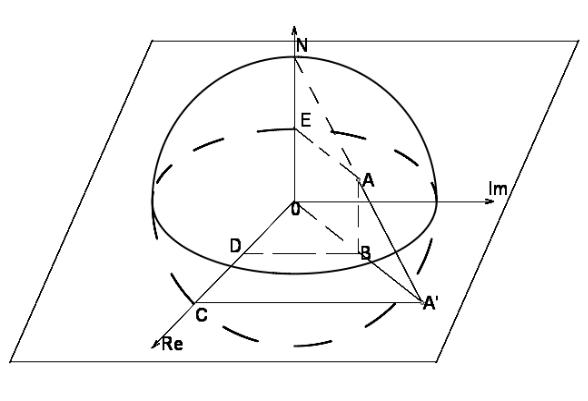
Рис. 2. |
|
|
|
|
|
|
|
|
|
||
З а д а ч а 2. Пусть |
x , y |
|
- координаты точки A' . Найти координаты |
ξ ,η ,ζ точки A. |
|||||||
Р е ш е н и е. Из решения предыдущей задачи следует ξ = x (1−ζ ) , η= y (1−ζ ) . |
|||||||||||
Поскольку |
ξ 2 +η2+ζ 2=1 |
, то x2 (1−ζ )2 + y2 (1−ζ )2+ζ 2=1 . Следовательно, . |
|||||||||
(x2 + y2 )(1−ζ )2=1−ζ 2 |
, отсюда |
(x2 + y2 )(1−ζ )=1+ζ , ζ = |
x2+ y2−1 |
|
. Окончательно |
||||||
x2 + y2+1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
имеем: ξ = |
2 x |
, η= |
2 y |
, ζ = |
x2 + y2−1 |
. ■ |
|
||||
x2 + y2 +1 |
x2+ y2+1 |
|
|
||||||||
|
|
|
|
x2 + y2 +1 |
|
||||||
З а м е ч а н и е 1. Из рассмотренных задач также следует биективность (то есть взаимная
однозначность) стереографической проекции |
S {N }→ . |
|
|
|||||
Пусть последовательность |
An' точек на S сходится к N (можно считать, что |
|||||||
(ξ n ,ζ n ,ζ n )→(0,0 ,1) , n→∞ , где (ξ n ,ζ n ,ζ n ) |
- координаты точки |
An' |
). Тогда образ этой |
|||||
последовательности |
A |
n |
стремится к |
∞ , так как |
A →∞ , см. п.1.1, Определение 11а. |
|||
|
|
|
|
|
n |
|
|
|
Обратно, если имеется такая последовательность комплексных чисел |
Bn |
такая, что |
||||||
Bn →∞, n→∞ , то последовательность |
Bn' |
на S, являющаяся её прообразом при |
||||||
59
стереографической проекции, стремится к N. Естественно поэтому пополнить плоскость
точкой ∞ , которую определим как образ N. |
||
О п р е д е л е н и е |
2. |
Комплексная плоскость, пополненная точкой ∞ указанным выше |
способом, называется расширенной (комплексной) плоскостью и обозначается через . |
||
|
|
̄ |
О п р е д е л е н и е |
3. |
Проколотой окрестностью точки ∞ называется открытое |
множество, целиком лежащее вне круга {z : z <r } при некотором положительном r. О п р е д е л е н и е 4. Окрестностью точки ∞ называется множество U {∞} , где U
— проколотая окрестность ∞ .
Расширенную комплексную плоскость часто удобно отождествлять со сферой Римана.
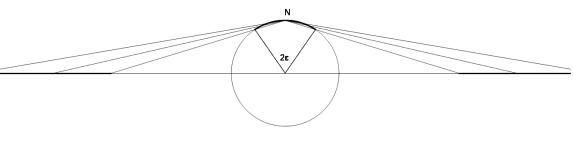
П р и м е р 1. На рис.3 изображена окрестность |
∞ - множество точек сферы, широта |
||
которых больше |
2 −ε , 0<ε<π . Её проекция на |
есть {z : z >r } {∞} |
, где |
|
π |
̄ |
|
r=ctg |
ε |
. |
|
2 |
|||
|
|
Рис.3. «Полярная шапка». |
|
|
Открытые и замкнутые множества в |
определяются так же, как и для , см. |
|
̄ |
|
на , а в Определении 3 в случае z0 =∞ |
Определения 3 и 4 п.1.2 (надо заменить |
|
|
|
|
̄ |
вместо ε-окрестности рассматривать просто окрестность ∞ ). Для точки ∞ определены некоторые арифметические операции.
∞±a=a±∞=∞ , a≠∞; |
|
|||||
|
∞ a =a ∞=∞ ∞=∞ , a≠0 ; |
|||||
О п р е д е л е н и е 5. |
a =0, ∞ =∞ , a≠∞; |
|
. |
|||
|
∞ |
a |
|
|
|
|
a |
|
|
|
|
|
|
=∞ , |
a≠0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
З а м е ч а н и е 2. Операции |
∞±∞ , ∞ 0 , |
0 |
, |
∞ |
не определяются. |
|
0 |
∞ |
|||||
|
|
|
|
|
|
|
60
Понятия непрерывного пути и непрерывной кривой на |
удобно вводить, рассматривая |
|
|
̄ |
|
сферу Римана. |
есть непрерывное отображение отрезка |
|
О п р е д е л е н и е 6. Непрерывный путь на |
||
̄ |
|
|
действительной прямой [α ,β], α β в S, то есть такое отображение γ :[ α ,β]→S , чей |
||
образ — непрерывная линия на S. Точки γ(α) |
и γ(β) |
называются началом и концом |
пути соответственно. Путь называется замкнутым, если его начало и конец совпадают. З а м е ч а н и е 3. Определение 6 не является «строгим», так как мы не определяли, что
такое «непрерывное отображение в S» и что такое «непрерывная линия на S». Будем считать всё это «интуитивно понятным».
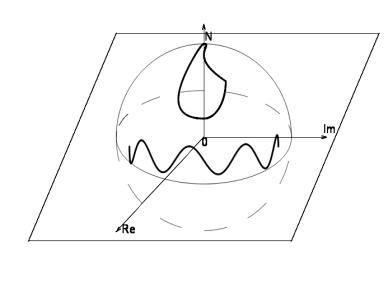
П р и м е р 2. На рис.4 приведены примеры образов непрерывных путей.
Рис.4. |
|
|
Так же, как и в случае |
, можно ввести понятие эквивалентных путей и непрерывной |
|
кривой, см. Определения 7, 8 п.1.2. |
|
|
О п р е д е л е н и е 6. |
Непрерывные пути |
γ1 :[ α1 ,β1 ]→S и γ2 :[α2 ,β2 ]→S называются |
эквивалентными, если существует непрерывная возрастающая взаимно-однозначная |
||
функция τ:[α1 , β1 ]→[α2 ,β2 ] такая, что |
γ2 (τ(t))=γ1(t), t [α1 , β1 ] . |
|
О п р е д е л е н и е 7. |
Кривой называется класс эквивалентных путей. |
|
П р и м е р 3. Действительная ось (и мнимая тоже), пополненная точкой ∞ , является замкнутой кривой в ̄ , см. рис.5.
61
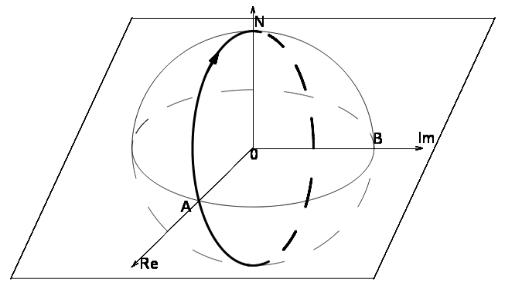
Рис.5.
Пусть имеются две пересекающиеся кривые на сфере, каждая из которых имеет касательный вектор в точке пересечения.
О п р е д е л е н и е 8. Углом между кривыми на сфере называется угол между их касательными векторами в точке пересечения, если глядеть из центра сферы.
З а д а ч а 3. Найти угол между действительной и мнимой осью в точке ∞ .
Р е ш е н и е. Действительная и мнимая оси представляют собой окружности, проходящие через полюса сферы S и ортогональные в южном полюсе (последний проецируется в точку 0). Следовательно, и в северном полюсе угол между ними будет прямой. Если глядеть на север из центра сферы, то направление вращения от касательного вектора действительной оси к касательному вектору мнимой оси в северном полюсе совпадает с вращением по
часовой стрелке, следовательно, искомый угол равен −π |
.■ |
2 |
|
З а д а ч а 4. Найти сумму внутренних углов сферического треугольника NAB (углы считаются положительными), см. рис.5.
Р е ш е н и е. Из предыдущей задачи следует, что действительная и мнимая оси пересекаются в северном полюсе под прямым углом. Они пересекают экватор (точки A и B) также под
прямым углом, следовательно, искомая сумма равна |
3 |
π |
. ■ |
|
2 |
|
определяются как образы |
З а м е ч а н и е 4. Окрестности U R точки ∞ на |
|||
|
|
̄ |
|
окрестностей точки N на S, то есть множества вида |
{z : z >R , R>0 } . Проколотая |
||
62
