
6.1.2.4. Определение перемещений при изгибе способом Верещагина
Если брус состоит из прямолинейных участков с постоянной в пределах каждого из них жесткостью, то интегралы Мора можно вычислять по способу Верещагина.
Определение
способом Верещагина перемещений
![]() (прогиба или угла поворота) некоторого
сечения балки (или рамы) ведут в следующей
последовательности:
(прогиба или угла поворота) некоторого
сечения балки (или рамы) ведут в следующей
последовательности:
строят независимо друг от друга эпюру изгибающих моментов (
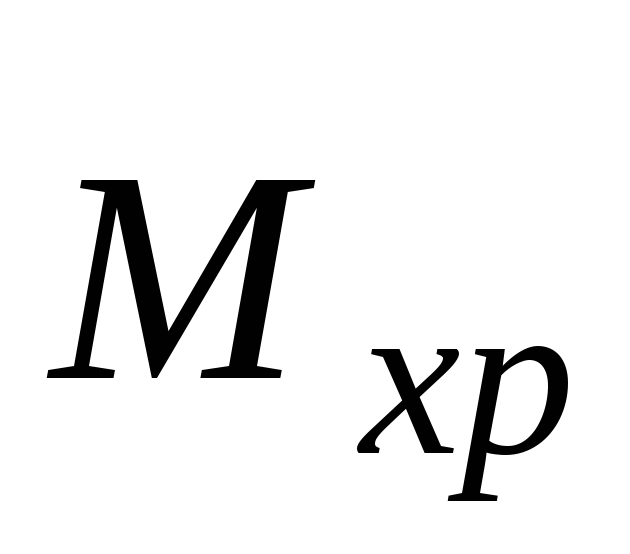 )
для «грузового» состояния и эпюру
изгибающих моментов (
)
для «грузового» состояния и эпюру
изгибающих моментов ( )
для «единичного» состояния, соответствующего
искомому перемещению;
)
для «единичного» состояния, соответствующего
искомому перемещению;обе эти эпюры разбивают на одинаковые участки, в пределах каждого из которых эпюра изгибающих моментов «единичного» состояния изменяется по монотонному линейному закону, а изгибная жесткость сечения балки (или рамы) постоянна;
эпюру изгибающих моментов «грузового» состояния разбивают на простейшие фигуры (прямоугольники, треугольники и т.п.), для каждой из которых определяют площадь
 ,
положение ее центра тяжести. Значения
площадей и положения их центров тяжести
для некоторых простейших фигур приведены
в табл.6.1.
,
положение ее центра тяжести. Значения
площадей и положения их центров тяжести
для некоторых простейших фигур приведены
в табл.6.1.
Таблица 6.1
|
Эпюра
|
Площадь
|
Координата центра
тяжести
|
|
|
|
|
|
|
|
|
Окончание табл. 6.1
|
|
|
|
под центром тяжести каждой площади
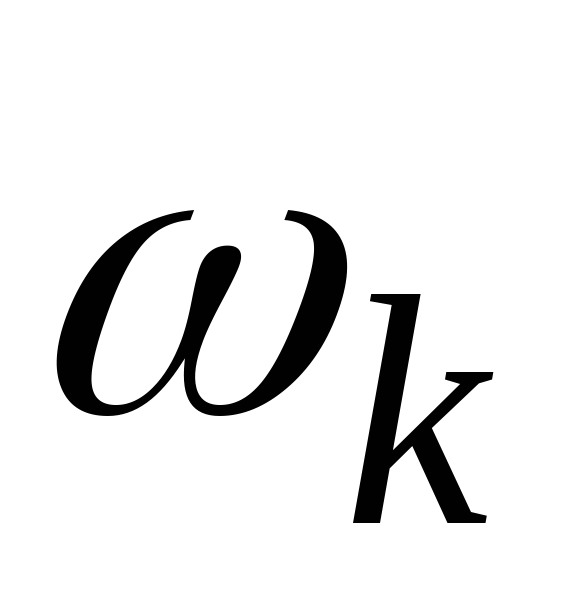 определяют ординату
определяют ординату на эпюре изгибающих моментов «единичного»
состояния;
на эпюре изгибающих моментов «единичного»
состояния;искомое перемещение определяется как алгебраическая сумма
![]() (6.17)
(6.17)
где k
– номер площади; m
– число простейших фигур, на которые
разбита эпюра изгибающих моментов
«грузового» состояния. Произведение
![]()
![]() считается положительным, если часть
эпюры изгибающих моментов «грузового»
состояния, имеющая площадь
считается положительным, если часть
эпюры изгибающих моментов «грузового»
состояния, имеющая площадь![]() ,
и соответствующая ей ордината
,
и соответствующая ей ордината![]() расположены по одну сторону от нулевой
линии.
расположены по одну сторону от нулевой
линии.
Положительное
значение перемещения
![]() получается в случае, если его направление
совпадает с направлением единичного
силового фактора (единичной силы или
момента).
получается в случае, если его направление
совпадает с направлением единичного
силового фактора (единичной силы или
момента).
6.2. Расчет статически определимых балок
Задача 1. Для
заданной схемы балки (рис 6.4) написать
выражения
![]() и
и![]() для каждого участка в общем виде,
построить эпюры
для каждого участка в общем виде,
построить эпюры![]() и
и![]() ,
найти
,
найти![]() и подобрать стальную балку двутаврового
поперечного сечения при []
= 1600 кг/см
и подобрать стальную балку двутаврового
поперечного сечения при []
= 1600 кг/см![]() =
160 МПа;q
= 1 т/м = 1
10
=
160 МПа;q
= 1 т/м = 1
10![]() Н/м; Р = 210
Н/м; Р = 210![]() Н; а = 2 м;b
= 4 м.
Н; а = 2 м;b
= 4 м.
Решение
Под действием приложенных нагрузок балка работает на изгиб. По условию задачи требуется провести проектный расчет. Из условия прочности по нормальным напряжениям (6.4)расчет ведется по соотношению
![]() .
.
Для определения
расчетного изгибающего момента max
![]() (в
опасном сечении) необходимо построить
эпюры поперечной силы
(в
опасном сечении) необходимо построить
эпюры поперечной силы
![]() и изгибающего момента
и изгибающего момента
![]() .
.
Определение реакций опор.
Определив типы опор и мысленно заменив их соответствующими реакциями (см. рис. 6.4а), установим их величины.
Так
как горизонтальные и наклонные силы
отсутствуют, то
![]() .
Для определения реакций
.
Для определения реакций![]() и
и![]() записываем
два уравнения равновесия.
записываем
два уравнения равновесия.

Рис. 6.4
Уравнение моментов всех сил относительно точки А
![]() ,
отсюда
,
отсюда
 .
.
Уравнение моментов всех сил относительно точки В
![]() отсюда
отсюда
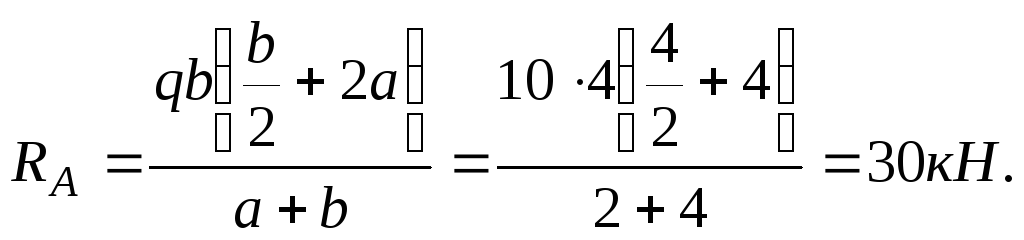
Обе реакции получились положительными. Это означает, что их действительное направление совпадает с выбранным. Для проверки правильности определения реакций опор спроектируем все внешние силы, приложенные к балке, на вертикальную ось Y:
![]()
Уравнение удовлетворяется тождественно, значит, реакции опор определены верно.
Построение эпюр поперечных сил и изгибающих моментов.
Разбиваем балку
на 4 участка. Границами участков являются
точки A,
B,
C,
D,
E.
Положение произвольного поперечного
сечения на участках характеризуется
соответствующими координатами
![]() ,
,![]() ,
,![]() ,
,![]() .
Записываем выражение для поперечных
сил и изгибающих моментов по участкам,
используя выражения (6.1), (6.2) и правила
знаков (см. рис. 6.2).
.
Записываем выражение для поперечных
сил и изгибающих моментов по участкам,
используя выражения (6.1), (6.2) и правила
знаков (см. рис. 6.2).
Участок 1: 0![]() b.
Рассматриваем часть балки, расположенную
по левую сторону от сечения с координатой
b.
Рассматриваем часть балки, расположенную
по левую сторону от сечения с координатой
![]() :
:
![]() ;
;
![]() .
.
Координата
![]() входит в выражение для
входит в выражение для![]() в первой степени (
в первой степени (![]() - линейная функция
- линейная функция![]() ).
Для построения эпюры
).
Для построения эпюры![]() достаточно определить значения ее
ординат на границах участков:
достаточно определить значения ее
ординат на границах участков:
![]() = 0,
= 0,
![]() =
=![]() =
30 кН;
=
30 кН;
![]() = b,
= b,
![]() =
=![]()
qb=
30
104
=
10 кН.
qb=
30
104
=
10 кН.
Изгибающий момент
![]() является квадратичной функцией
является квадратичной функцией![]() .
Для построения квадратичной параболы
необходимо определить как минимум три
значения изгибающего момента, два из
которых определяем на границах участков:
.
Для построения квадратичной параболы
необходимо определить как минимум три
значения изгибающего момента, два из
которых определяем на границах участков:
![]() = 0,
= 0,
![]() =
0;
=
0;
![]() = b,
= b,
![]() =
=![]() кНм.
кНм.
Так как поперечная
сила
![]() ,
меняя знак в одном из сечений (обозначим
его через
,
меняя знак в одном из сечений (обозначим
его через![]() ),
обращается в нуль, то в соответствии с
дифференциальными зависимостями (6.3)
изгибающий момент в этом сечении будет
иметь экстремум. Приравнивая выражение
),
обращается в нуль, то в соответствии с
дифференциальными зависимостями (6.3)
изгибающий момент в этом сечении будет
иметь экстремум. Приравнивая выражение![]() нулю, определяем координату сечения
нулю, определяем координату сечения![]() :
:
![]() ;
;
![]() =
=![]() м.
м.
Подставляя значение
![]() = 3 м в выражение
= 3 м в выражение![]() ,
определим экстремальное (максимальное)
значение изгибающего момента на этом
участке
,
определим экстремальное (максимальное)
значение изгибающего момента на этом
участке
![]() кНм.
кНм.
Найденное
значение изгибающего момента будет
третьим значением ординаты эпюры
![]() для построения параболы.
для построения параболы.
Участок
2: 0![]() а.
Рассматриваем равновесие части балки,
расположенной слева от сечения с
координатой
а.
Рассматриваем равновесие части балки,
расположенной слева от сечения с
координатой
![]() :
:
![]() кН;
кН;
![]() (
(![]() - линейная функция
- линейная функция![]() );
);
![]() =
0,
=
0,
![]() кНм;
кНм;
![]() =а,
=а,
![]() кНм.
кНм.
Участок
3: 0![]() а.
Рассматриваем равновесие части балки,
расположенной справа от сечения с
координатой
а.
Рассматриваем равновесие части балки,
расположенной справа от сечения с
координатой
![]() :
:
![]() кН;
кН;
![]()
![]() = 0,
= 0,![]() =
0;
=
0;
![]() =
а,
=
а,
![]() =
- 40 кНм.
=
- 40 кНм.
Участок
4: 0![]() а.
Рассматриваем равновесие части балки,
расположенной справа от сечения с
координатой
а.
Рассматриваем равновесие части балки,
расположенной справа от сечения с
координатой
![]() :
:
![]() кН;
кН;
![]()
![]() =0,
=0,
![]() кНм;
кНм;
![]() =а,
=а,
![]() кНм.
кНм.
Строим
эпюру
![]() (см. рис. 6.4 б), располагая ее строго под
схемой балки. Положительные значения
(см. рис. 6.4 б), располагая ее строго под
схемой балки. Положительные значения![]() откладываем выше нулевой линии (которая
проводится параллельно оси балки), а
отрицательные - ниже.
откладываем выше нулевой линии (которая
проводится параллельно оси балки), а
отрицательные - ниже.
Строим
эпюру изгибающих моментов, располагая
ее строго под эпюрой
![]() (см. рис. 6.3 в). Положительные значения
(см. рис. 6.3 в). Положительные значения![]() откладываем выше нулевой линии,
отрицательные – ниже. Используя
дифференциальные зависимости (6.3) и
правила, вытекающие непосредственно
из метода сечений, проводим проверку
правильности построения эпюр
откладываем выше нулевой линии,
отрицательные – ниже. Используя
дифференциальные зависимости (6.3) и
правила, вытекающие непосредственно
из метода сечений, проводим проверку
правильности построения эпюр![]() и
и![]() .
Устанавливаем изгибающий момент в
опасном сечении
.
Устанавливаем изгибающий момент в
опасном сечении![]() кНм.
кНм.
3. Подбор размеров поперечного сечения балки.
Подбор сечения балки ведем из условия прочности (6.4)
![]() см
см![]() .
.
Используя таблицу
сортамента прокатной стали для двутавров
1,
по значению осевого момента сопротивления
![]() выбираем двутавр № 24, у которого
выбираем двутавр № 24, у которого![]() 289 см
289 см![]() .
.
Задача 2. Для
заданной расчетной схемы (рис. 6.5 а)
подобрать из условия прочности деревянную
балку круглого поперечного сечения при
=
80 кг/см![]() =
8 МПа; а = 0,5 м;q
= 2 т/м = 20 кн/м; М = 1 тм = 10 кНм.
=
8 МПа; а = 0,5 м;q
= 2 т/м = 20 кн/м; М = 1 тм = 10 кНм.
Решение
Под действием нагрузок, приложенных к балке, она работает на изгиб. По условию задачи требуется провести проектный расчет. Из условия прочности по нормальным напряжениям (6.4) расчет ведем по соотношению
![]()
![]()
Учитывая, что для
круглого сечения
![]() получим
получим
![]()
Для определения
расчетного изгибающего момента max
M![]()
необходимо построить эпюры поперечной
силы
необходимо построить эпюры поперечной
силы
![]() и изгибающего момента M
и изгибающего момента M![]() .
.

Рис. 6.5
1. Определение реакции опор.
Так как балка имеет
опору только с одной стороны, то нет
необходимости определять реакции в
опоре в связи с тем, что эпюры
![]() и
M
и
M![]() можно построить, проводя рассмотрение
от свободного конца балки.
можно построить, проводя рассмотрение
от свободного конца балки.
2. Построение эпюр поперечных сил и изгибающих моментов.
Разбиваем балку
на три участка (см. рис. 6.5 а). Границами
участков являются сечения A,
B,
C,
D.
Положение произвольного поперечного
сечения на участках характеризуется
координатами
![]()
![]()
![]() Применяя метод сечений и рассматривая
равновесие части балки, не содержащей
защемления, записываем выражения для
поперечных сил и изгибающих моментов
по участкам.
Применяя метод сечений и рассматривая
равновесие части балки, не содержащей
защемления, записываем выражения для
поперечных сил и изгибающих моментов
по участкам.
Участок 1: 0
![]()
2а.
2а.
![]() =
q
=
q![]() ;
;![]() =
0,
=
0,
![]() =
0;
=
0;
![]() =
2а,
=
2а,
![]() =
q2a
= 2020,5
=
=
q2a
= 2020,5
=
= 20 кН;
M![]() =
=
![]()
![]()
![]() =
0,M
=
0,M![]() =
0;
=
0;
![]() =
2а,
=
2а,
M![]()
![]() кНм.
кНм.
Так как поперечная
сила
![]() не меняет знак на рассматриваемом
участке, то в качестве третьей точки
для построения эпюры M
не меняет знак на рассматриваемом
участке, то в качестве третьей точки
для построения эпюры M![]() можно взять, например,
можно взять, например,
![]() =
а, тогда
=
а, тогда
M![]() =
=
![]() кНм.
кНм.
Участок 2: 0
![]()
а.
а.
![]() кН;
кН;
M![]()
![]() =
0,M
=
0,M![]() кНм;
кНм;
![]() =
а, M
=
а, M![]() кНм.
кНм.
Участок 3: 0
![]()
а.
а.
![]() кН;
кН;
M![]()
![]() =0,
=0,
![]() кНм;
кНм;
![]() =а,
=а,
![]()
= –20 кНм.
По полученным
значениям строим эпюры
![]() (см. рис. 6.5б) и M
(см. рис. 6.5б) и M![]() (см.
рис. 6.5в).
(см.
рис. 6.5в).
Используя
дифференциальные зависимости (6.3) и
правила, вытекающие непосредственно
из метода сечений, проводим проверку
правильности построения эпюр
![]() и M
и M![]() .
.
Устанавливаем
изгибающий момент в опасном сечении
max
M![]() =
20 кНм.
=
20 кНм.
3. Подбор размеров сечения балки.
Диаметр балки
![]() мм.
мм.
Принимаем d = 295 мм.
6.2.1. Вопросы для самопроверки и задачи для самостоятельного решения
Вопросы для самопроверки
Какой вид деформирования называют плоским прямым изгибом?
Чем отличается чистый изгиб от поперечного?
Как определяется изгибающий момент, возникающий в поперечном сечении балки?
Как определяется поперечная сила, возникающая в поперечном сечении балки?
Какое правило знаков принято для изгибающего момента и поперечной силы?
Какие дифференциальные зависимости установлены Д.И.Журавским для поперечного изгиба?
Как определяют нормальные напряжения при плоском прямом изгибе?
Как проводится расчет на прочность при изгибе по нормальным напряжениям?
Как и в каких случаях проводится расчет на прочность по касательным напряжениям?
Какие формы поперечных сечений являются рациональными для балок из пластичных материалов?
Задачи для самостоятельного решения
1 – 5. Для заданной
расчетной схемы стальной балки, приняв
а = 1 м, q=
10 кН/м,
= 160 МПа, построить эпюры поперечных сил
![]() ,
изгибающих моментов M
,
изгибающих моментов M![]() и подобрать поперечное сечение в форме:
1) швеллера (рис. 6.6,а), 2) квадрата (рис.
6.6,б), 3) двутавра (рис. 6.6,в), 4) круга (рис.
6.6,г), прямоугольника (рис. 6.6,д), для
которого h
= 2в.
и подобрать поперечное сечение в форме:
1) швеллера (рис. 6.6,а), 2) квадрата (рис.
6.6,б), 3) двутавра (рис. 6.6,в), 4) круга (рис.
6.6,г), прямоугольника (рис. 6.6,д), для
которого h
= 2в.

Рис. 6.6



