Решение

Воспользуемся уравнением Эйнштейна для фотоэффекта (5Ф)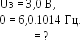

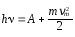^,(1)

где постоянная Планка h= 6,63^.10^–34Дж^.с;–искомая частота света. Красная граница фотоэффекта₀ равна такой частоте, при которой максимальная скоростьv_m=0. Тогда приn= n₀ уравнение (1) примет вид:

. (2)

По условию задачи при задерживающем напряжении U_зсамые быстрые электроны, имеющие скоростьv_m, полностью задерживаются электрическим полем, т. е. максимальная кинетическая энергия таких электронов равна работе электрического поля:, где е=1,6^.10^–19Кл–элементарный заряд, равный модулю заряда электрона. Тогда уравнение (1) с учетом (2) запишется:

,

откуда искомая частота света

Гц.

Пример 4.Фотон с энергией ε =250 кэВ рассеялся под углом α= 120^ºна первоначально покоившемся свободном электроне. Найти энергию рассеянного фотона ε'.

Решение

Энергию рассеянного ε' и падающего ε фотонов можно выразить через постоянную Планка h, скорость света в вакуумеси длину волны рассеянного λ' и падающего λ фотонов

(1)

Рассеяние фотона на электроне описывается формулой Комптона (7Ф), в которой 1 –cosα=2sin²(α/2),

. (2)

Подставим в эту формулу длины волн λ' и λ, найденные из (1), и из полученного уравнения выразим искомую энергию ε'

Учитывая числовые данные задачи и энергию покоя электрона mc²=0,51 МэВ, получим числовой ответ:

ε' =0,144 МэВ.

Пример 5.Атом водорода в основном состоянии поглотил фотон с длиной волны λ=0,122 мкм. Найти радиус электронной орбиты возбужденного атома.

Решение

Для нахождения радиуса электронной орбиты используем теорию Бора для атома водорода. Согласно первому постулату Бора (8Ф) электрон в атоме водорода движется только по стационарным орбитам, радиусы r_nкоторых удовлетворяют правилу квантования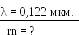

mvr_n =nh/2π,n=1, 2, 3,… (1)

К электрону в атоме водорода применим второй закон Ньютона ma_n = F_K , гдеa_n=v²/r_n–нормальное (центростремительное) ускорение; F_K=e²/4π₀r_n²–кулоновская сила, действующая на электрон. В результате второй закон Ньютона запишется:

(2)

где e–элементарный заряд, равный модулю заряда электрона; ε₀ –электрическая постоянная. Из уравнений (1), (2) находим радиус электронной орбитыr_n

(3)

где

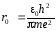(4)

постоянная величина (радиус Бора), равная r₀ =5,31^.10^–11 м, находится из таблицы. В результате радиус электронной орбиты (3) можно выразить через радиус Бора

r_n =r₀n². (5)

Квантовое число nнайдем из формулы Бальмера (см. (11Ф))

(6)

где R=1,10^.10⁷м^–1– постоянная Ридберга, находится из таблицы;m, n–квантовые числа. У насm=1, т. к. атом находился в основном состоянии. Тогда из (6) получимn =2. Подставляя это число в (5), найдем радиус электронной орбиты возбужденного атома:

r_n=2,12^.10^–10м= 0,212 нм.

Пример 6. Найти циклическую частоту ω вращения электрона на круговой орбите водородоподобного иона гелия Не⁺при главном квантовом числеn =2. С какой линейной скоростьюvвращается электрон на заданной орбите?

Решение

_{Воспользуемся вторым законом Ньютона} ma_n=F_к, гдеm=9,11^.10^–31кг–масса электрона;a_n =ω² r_n–нормальное (центростремительное) ускорение электрона;r_n – радиусn–й круговой орбиты электрона; 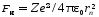–кулоновская сила, действующая на электрон;Z – зарядовое число, для гелия Z = 2;е, ε₀ –элементарный заряд (равен модулю заряда электрона) и электрическая постоянная (берутся из таблицы). В результате второй закон Ньютона запишется_:

(1)

Используем, далее, первый постулат Бора (8Ф) mvr_n =nħ, где v = ωr_n ^– линейная скорость электрона на заданной круговой орбите иона гелия;ħ =1,05^.10^–34Дж^.с–постоянная Планка. Тогда первый постулат Бора примет вид:

(2)

Решая систему уравнений (1), (2), получим:

(3)

где постоянная величина r₀ =4πε₀ħ²/me²=5,31^.10^–11м называется радиусом Бора (берется из таблицы). В результате (3) запишется:

r_n =r₀n²/Z. (4)

Подставляя это выражение в (2), найдем искомую циклическую частоту:

(5)

Используя табличные данные и условие задачи, найдем числовое значение циклической частоты или угловой скорости электрона:

ω =2,1^.10¹⁶ с^–1.

Линейная скорость электрона находится из формулы v = ωr_n. Учитывая (4) и (5), получим:

Пример 7. С какой минимальной кинетической энергией должен двигаться атом водорода, чтобы при неупругом лобовом (центральном) столкновении с другим, покоящимся атомом водорода, один из них оказался способным испустить фотон? Предполагается, что до столкновения оба атома находились в основном состоянии.