1)Тождественные преобразования и применение таблиц 1 и 2.

Пример 1. Найти оригинал для изображения

Решение.

Преобразуем на основании теоремы смещения: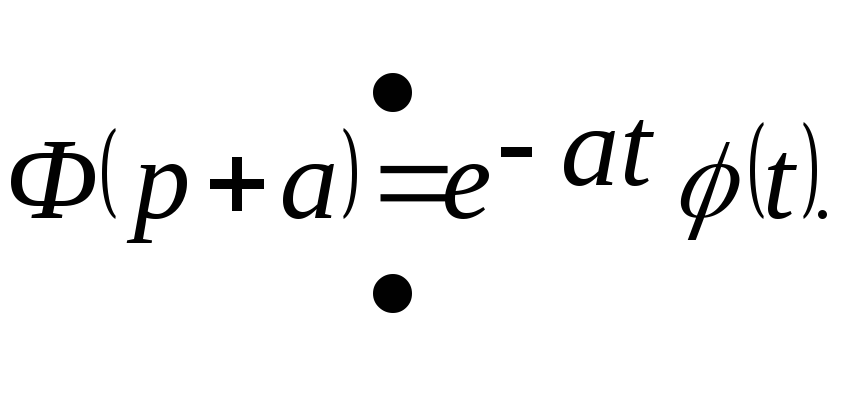имеем

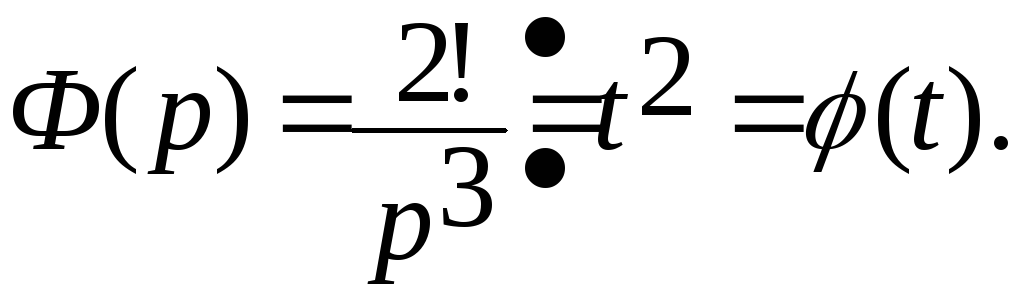
Тогда,

Пример 2. Найти оригинал для изображения

Решение.

Пример 3. Найти оригинал для изображения

Решение.

Пример 4. Найти оригинал для изображения

Решение.

Пример 5. Найти оригинал для изображения

Решение.

Пример 6. Найти оригинал для изображения

Решение.

Пример 7. Найти оригинал для изображения

Решение.

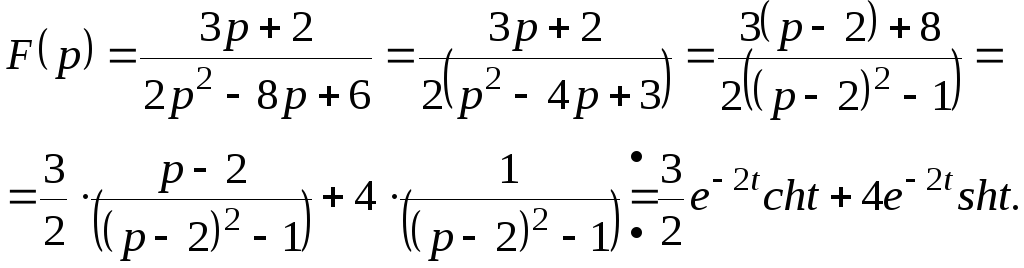
Пример 8. Найти оригинал для изображения

Отсюда следует равенство

Для нахождения используем метод частных значений.

При:

поэтому

Пример 9. Найти оригинал для изображения

Решение.

Отсюда следует равенство:

При:

Приравнивая коэффициенты приполучим:

Тогда

Пример 10. Найти оригинал для

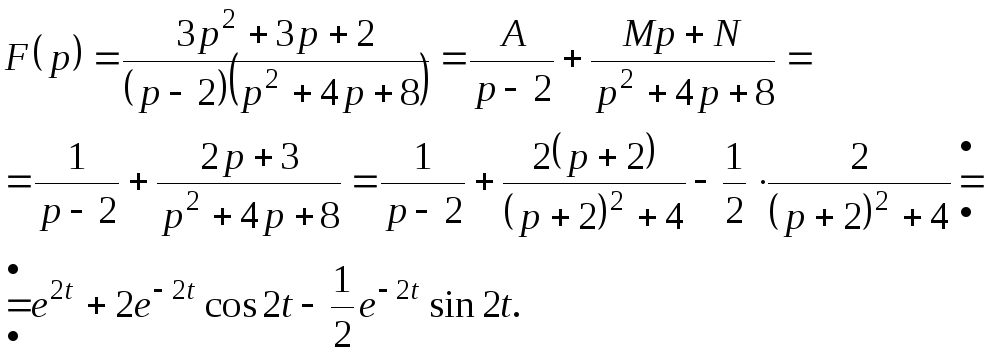
Пример 11. .Найти оригинал для .

Решение.

Так как ,, то по теореме Бореля

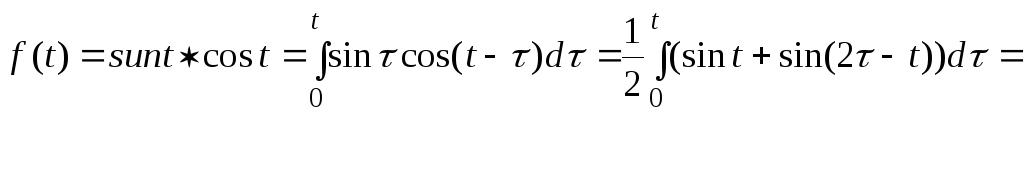
Пример 12. Найти оригинал для изображения

Решение.

Так как ,, то используя интеграл Дюамеля, получим

Вычислим:

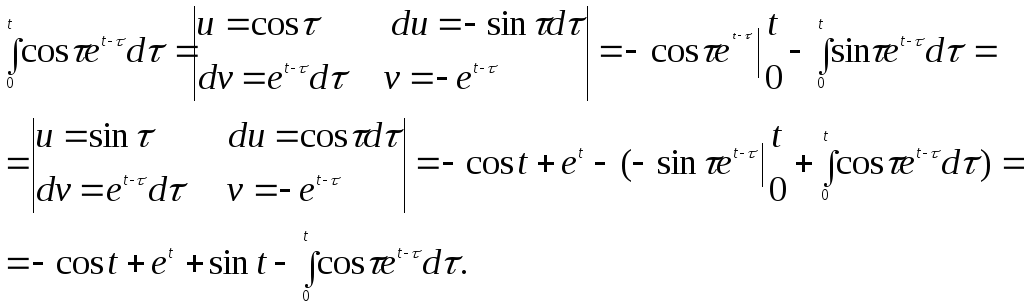
Отсюда:

Этот пример можно решить иначе.

Отсюда следует равенство:

Тогда:

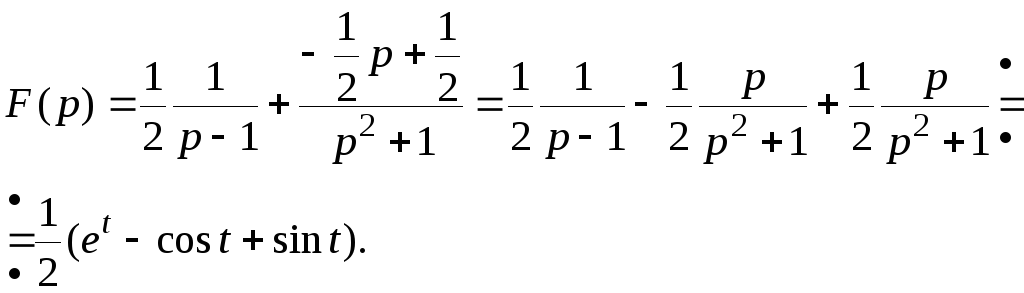
2) Вычисление оригиналов с помощью вычетов.

Будемпредполагать, что функция аналитическая во всей комплексной плоскостиp, за исключением, конечного числа особых точек и удовлетворяет условию , а также предполагается аналитичностьв бесконечно удаленной точке. Для вычисленияпоступим следующим образом. Возьмем контур Г, состоящий из дугиBA окружности и отрезкаAB (рис.7.2).

Радиус R выберем таким большим, чтобы все особые точки попали в область, ограниченную контуром Г, тогда:

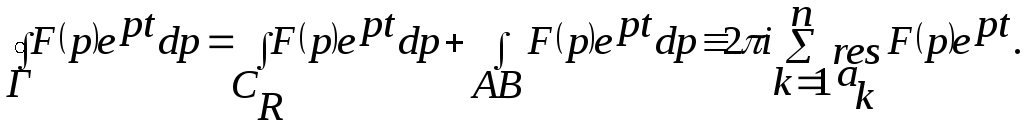
Особый интерес представляет собой случай, когда приисчезает.

Лемма Жордана.

Если настремится к нулю приравномерно относительно, то для любого

Итак, при и выполнении условия леммы Жордана имеем

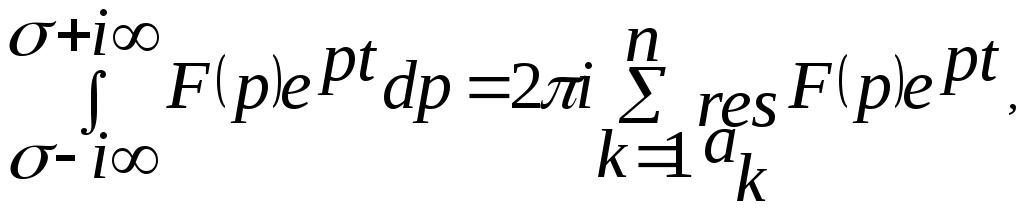откуда по формуле обращения получим:

(7.2)

Формулу (7.2) называют второй теоремой разложения. Она позволяет в самом общем случае найти оригинал по его изображению. Но очень часто F(p) представляет собой дробно-рациональную функцию, что позволяет упростить вычисления оригиналов.

Пусть

,

где А(р) и В(р)- многочлены степени m и n, соответственно, причем m<n.

1.Случай простых полюсов.

Применяя формулу для нахождения вычета относительно простого полюса от функции представимой в виде частного двух выражений, получим:

(7.3)

Здесь простые полюса.

2.Случай кратных полюсов.

Пусть - полюсы кратностии таких различных полюсов будетl, тогда

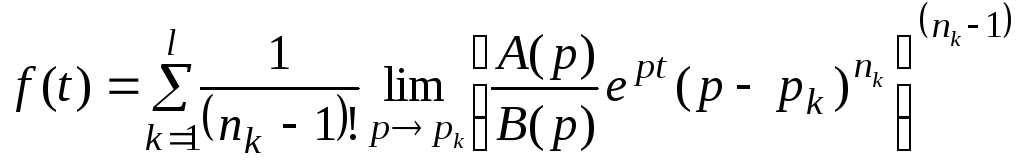(7.4)

3.Случай комплексно – сопряженных полюсов:

Пусть имеет простые комплексно – сопряженные корнии. Мы знаем, что комплексно- сопряженные корни появляются парами, а т.к. мы рассматриваем полиномыА(р) и В(р) с действительными коэффициентами, то после подстановки корней получим сопряженные выражения т.е.

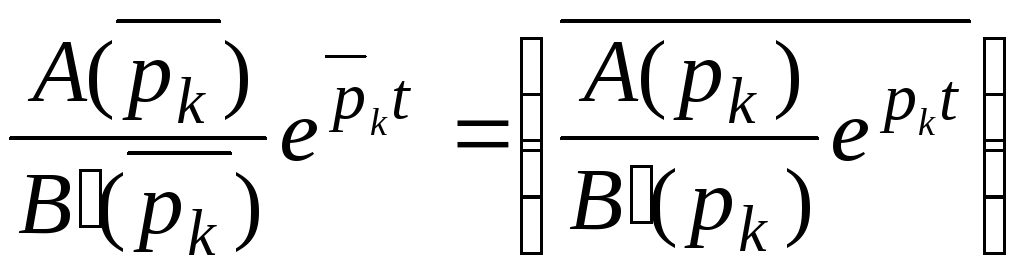
Теперь после подстановки корней в (7.3) мы получим, что выражение от пары комплексно- сопряженных корней дают:

.

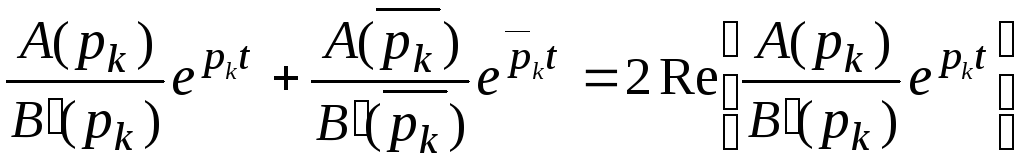В результате получим формулу для данного случая

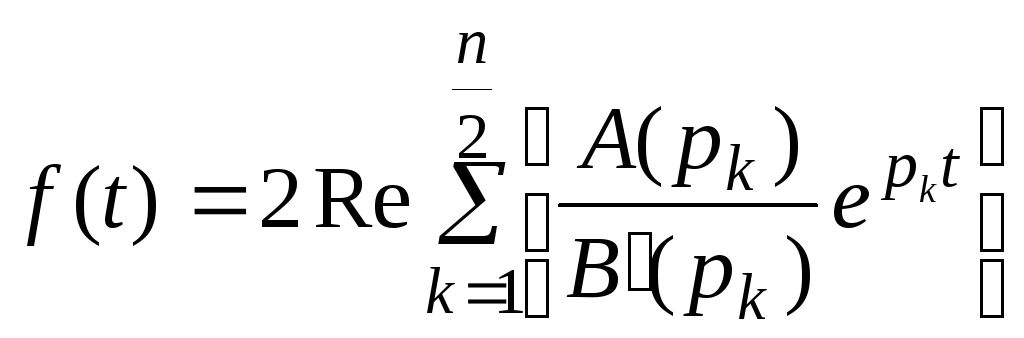(7.5)

Рассмотрим примеры нахождения оригиналов.

Пример 1. Найти оригинал для изображения

.

Решение.

Пример 2. Найти оригинал для изображения

Решение.

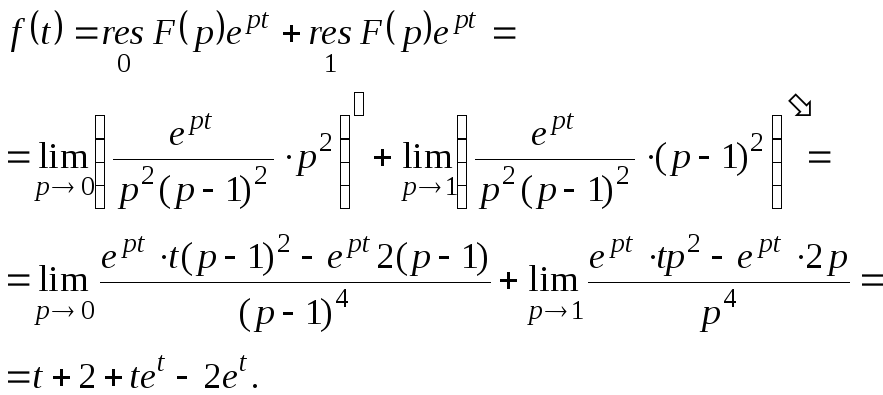
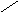
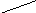
Пример 3. Найти оригинал для изображения

Решение. Так как изолированные особые точки иполюса второго порядка являются комплексно сопряженными, то

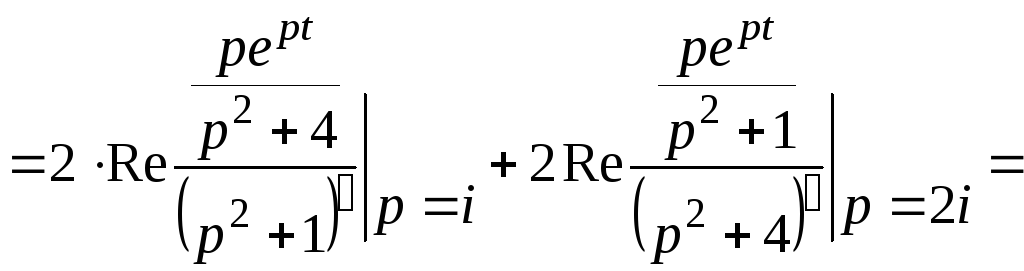
Пример 4. Найти оригинал, если дано изображение

Решение.

1 способ

Преобразуем 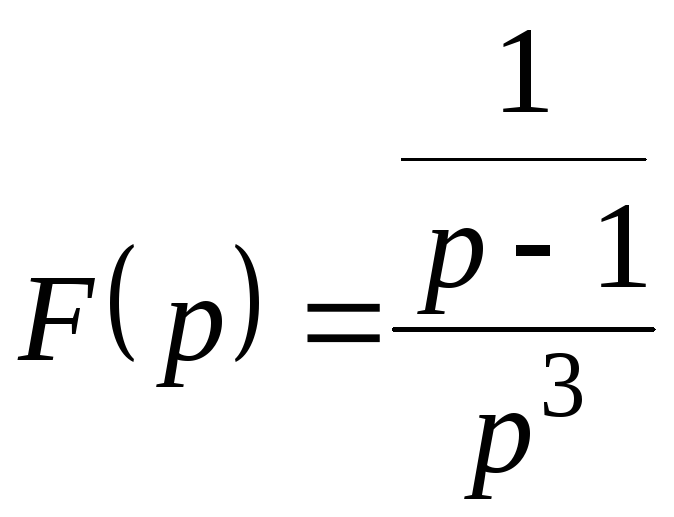, и воспользуемся теоремой интегрирования оригинала:

Так как то

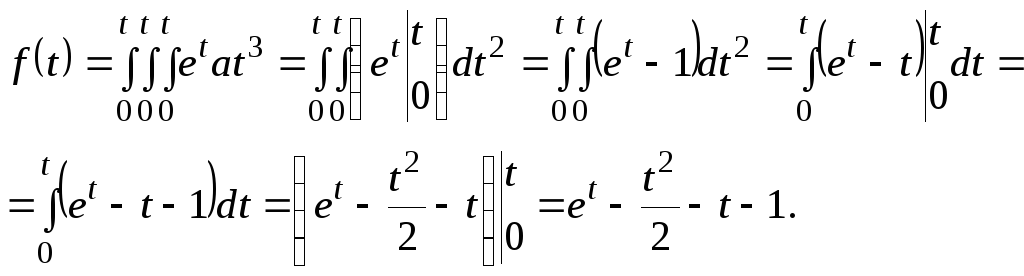
2 способ

Преобразуем

.

тогда .

3 способ

Так как имеет две изолированные особые точки:- простой полюс и- полюс третьего порядка, то

Найдем:

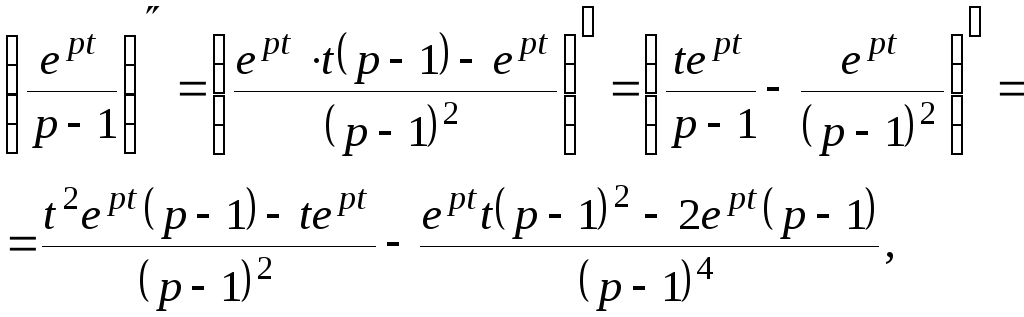
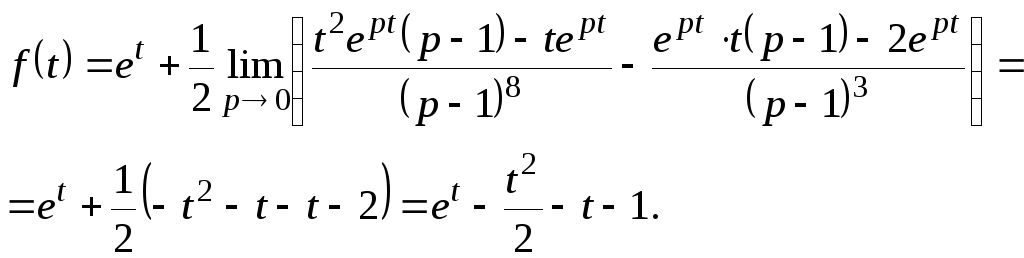
4 способ

Так как аипо теореме Бореля