
- •Введение
- •1. Понятие оригинала
- •2. Изображение по лапласу
- •3. Изображения простейших элементарных функций
- •4.Свойства преобразования лапласа
- •2С) Теорема подобия
- •3C) Теорема затухания (Теорема смещения)
- •5C) Теорема опережения.
- •10С) Интегрирование изображений.
- •11С) Теорема умножения изображений (теорема Бореля)
- •12С) Умножение оригиналов.
- •5.Примеры нахождения изображений с помощью таблиц 1 и 2
- •6. Импульсные функции и их изображения
- •7.Формула обращения преобразования лапласа
- •1)Тождественные преобразования и применение таблиц 1 и 2.
- •2) Вычисление оригиналов с помощью вычетов.
- •8.Применение преобразования лапласа для решения уравнений и систем
- •8.1 Решение линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.2 Решение дифференциальных уравнений с постоянными коэффициентами с помощью интеграла Дюамеля.
- •8.3 Решение дифференциальных уравнений с переменными коэффициентами.
- •8.4 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.5 Линейные дифференциальные уравнения с запаздывающим аргументом.
- •8.6 Интегральные уравнения типа «свертки».
- •8.7 Линейные интегро-дифференциальные уравнения.
- •9.Решение диференциальных уравнений в частных производных и задач математической физики
- •10. Применение операторных методов для анализа линейных систем
- •11. Дискретное преобразование лапласа. Z – преобразование лорана
- •1) Решетчатые функции.
- •2) Конечные разности решетчатых функций.
- •3) Суммирование решетчатых функций.
- •4) Определение дискретного преобразования Лапласа.
- •5) Формула обращения.
- •1С) Теорема линейности.
- •Библиографический список
- •Оглавление
4.Свойства преобразования лапласа
1с) Линейность.
Пусть
функции
![]() являются оригиналами. Соответствующие
им изображения обозначим
являются оригиналами. Соответствующие
им изображения обозначим![]() .
Тогда для любых комплексных чисел
.
Тогда для любых комплексных чисел![]() ,
,![]() функция
функция![]() также является оригиналом с изображением
также является оригиналом с изображением![]() и справедливо равенство:
и справедливо равенство:
![]()
Заметим,
что для
![]() существенно, что все
существенно, что все![]() ,
,![]() - оригиналы, так как, например, функция
- оригиналы, так как, например, функция![]() является оригиналом, а слагаемые
является оригиналом, а слагаемые![]() и
и![]() не являются.
не являются.
Справедливо
и обратное утверждение: если
![]() - изображения, то
- изображения, то
![]()
Здесь
также важно, что
![]() ,
,![]() - изображения, так как, например,
- изображения, так как, например,![]() является изображением, а слагаемые
является изображением, а слагаемые![]() и
и![]() не являются.
не являются.
Используя свойство линейности, можно значительно проще найти изображения тригонометрических и гиперболических функций, например:
а)
![]() итак
итак
![]() .
.
2С) Теорема подобия
Для
любого
![]() имеет место соотношение
имеет место соотношение
![]()
Доказательство:
Пусть
![]()
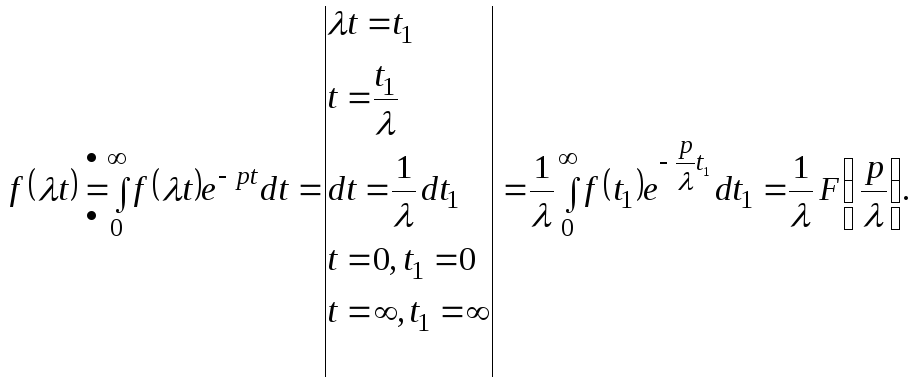
Следствие:
![]()
3C) Теорема затухания (Теорема смещения)
Для
любого
![]() имеет место соотношение
имеет место соотношение
![]()
Умножение
оригинала на функцию
![]() влечет смещение переменнойр
на
влечет смещение переменнойр
на ![]() .
.
![]()
Следствие:
![]()
4с) Теорема запаздывания.
Для
любого постоянного
![]() :
:
![]()
.
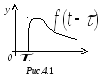
t
Т.о.
запаздывание оригинала на время
![]() соответствует умножение изображения
на
соответствует умножение изображения
на![]() (рис.4.1).
(рис.4.1).
Доказательство:

![]()
Теорема запаздывания играет важную роль в связи с тем, что с ее помощью можно получать изображения функций часто встречающихся в технических приложениях - функций, которые имеют различные аналитические выражения в различных промежутках значений аргумента.
Пример. Найти изображение единичного импульса:
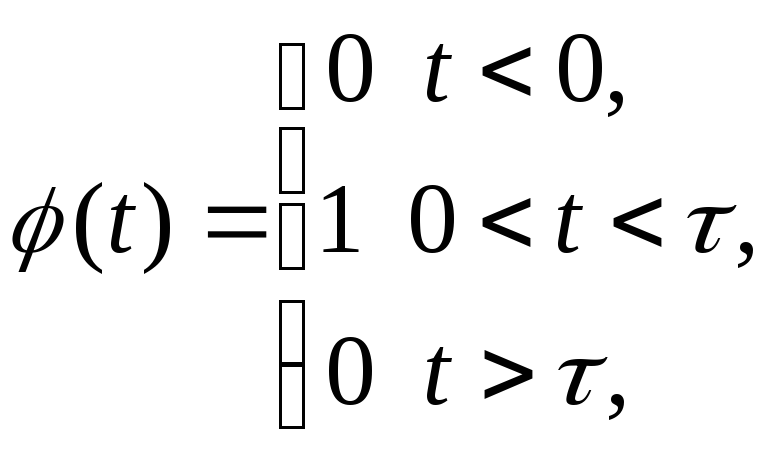 (рис.4.2).
(рис.4.2).
![]()
Итак,
![]()

П ример.
Найти изображение единичного импульса
длительного
ример.
Найти изображение единичного импульса
длительного![]() ,
начинающегося в момент времени
,
начинающегося в момент времени![]() (рис.4.3).
(рис.4.3).
Эту
функцию можно представить как предыдущую,
сдвинутую на
![]() ,
т.е. нужно найти изображение функции
,
т.е. нужно найти изображение функции![]() ,
если изображение функции
,
если изображение функции![]() ,
,
![]()
Пример. Найти изображение последовательности импульсов (рис.4.4).

![]()
итак
![]()

5C) Теорема опережения.
 (рис.4.5).
(рис.4.5).

![]()

6c) Дифференцирование оригинала.
![]() .
.
Т.о.
дифференцирование оригинала сводится
к умножению его изображения на p
и вычитанию f(0).
В частности если f(0)=0,
то
![]() .
Заметим, чтоf(0)=f(+0).
.
Заметим, чтоf(0)=f(+0).
Доказательство:

Применим теорему повторно:

 и
т.д.
и
т.д.
![]()
Если![]() ,
то
,
то![]()
т.е.
при нулевых начальных условиях n-кратное
дифференцирование оригинала сводится
к умножению на
![]() его
изображения.
его
изображения.
Пример.
Найти изображение функции
![]() .
.
Решение:
Пусть
![]() ,
тогда
,
тогда![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
откуда:
,
откуда:
![]() ,
,
то
есть
![]() .
.
7с) Предельное соотношение для изображений.
Из теоремы дифференцирования вытекают два важных следствия:
α)
Если
![]() является оригиналом, а
является оригиналом, а![]() - функция аналитическая в бесконечности,
то
- функция аналитическая в бесконечности,
то
![]() .
.
Действительно,
ранее мы показали, что любое изображение,
аналитическое в бесконечности стремится
к нулю при
![]() .
В частности
.
В частности
![]() ,
,
![]() ,
,
Откуда
и вытекает свойство
![]() .
.
Нетрудно
показать теперь:
![]() .
.
б)
Если
![]() является оригиналом и существует предел
функции f(t)
при
является оригиналом и существует предел
функции f(t)
при
![]() :
:
![]() ,
то
,
то
![]() .
.
Действительно:
![]()
![]() ,
,
![]() ,
,
![]() ,
ч.т.д.
,
ч.т.д.
8с) Интегрирование оригинала.
Если
![]() и
и![]() ,
то
,
то
![]() .
.
Т.е. интегрирование оригинала в пределах от 0 до t приводит к делению изображения на р.
Доказательство:
Заметим,
что
![]() ,
,![]() .
.
Пусть
![]() .
.
Найдем
изображение производной
![]() .
.
![]()
В то же время
![]()
Приравнивая правые части, получим
![]() ,
,
т.е.
![]() .
.
Важнейшее свойство преобразования Лапласа- это то, что сложным действиям дифференцирования и интегрирования в пространстве оригиналов соответствуют простые алгебраические действия умножения и деления на р в пространстве изображений.
9с) Дифференцирование изображений.
![]()
т.о. дифференцирование изображения сводится к умножению оригинала на (–t).
Доказательство:
![]() ,
,
![]() .
.
Справа
стоит интеграл Лапласа для функции
![]() ,т.е.
,т.е.
![]()
Применяя теорему n раз получим
![]()
Пример.
Найти изображение степенной функции
![]() ,
используя 9с).
,
используя 9с).
Если
![]() ,
то получить формулу можно последовательным
дифференцированием и умножением на –t.
,
то получить формулу можно последовательным
дифференцированием и умножением на –t.

![]()
![]() .
.
Повторяем умножение – дифференцирование.
![]()
По индукции нетрудно получить формулу
![]() .
.
С
помощью Г функции формулу можно
распространить на любые
![]() .
.
 .
.
