6.4. Надежность системы при раздельном резервировании и с целой кратностью по всем элементам
Расчетная схема надежности для этого случая изображена на рис. 6.13.
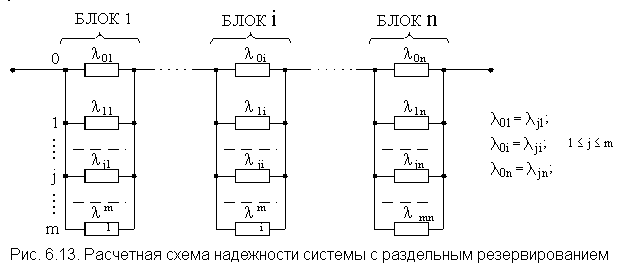
Отказ этой системы может произойти при отказе любого блока. Совпадение работоспособных состояний n блоков системы гарантирует работоспособное состояние системы. Следовательно, если известны вероятности безотказной работы каждого из блоков, то вероятность безотказной работы системы выражается формулой
.
(6.21)
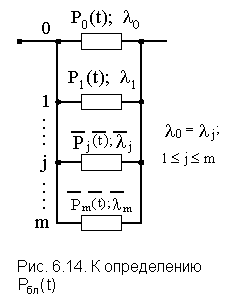
Воспользуемся результатом расчетов в подразд. 6.1 (см. рис. 6.2). При преобразовании схемы (рис. 6.2) в более удобную схему (рис. 6.14) вероятность безотказной работы каждой из цепей определяется по формуле (6.1). Для элементов схемы (рис. 6.14) принято:
;
.
Сравнивая структуру одного блока схемы по рис. 6.13 и 6.14 видим, что они идентичны. Следовательно, вероятность безотказной работы системы при раздельном резервировании с целой кратностью определится по выражению произведения вероятностей безотказной работы блоков:
,
(6.22)
Где λ0k- интенсивность отказов основного элемента k-го блока; выражение в фигурных скобках - вероятность безотказной работы k-го блока.
Среднее время наработки до отказа соответственно найдется по выражению
.
При равнонадежных элементах и одинаковой кратности их резервирования по всем блокам [13, 15] расчетные выражения оценки важнейших показателей надежности такой системы примут вид:
,
(6.23)
Где
для всех элементов системы.
,
(6.24)
Где
.
6.5. Смешанное резервирование неремонтируемых систем
На практике очень часто приходится повышать надежность отдельных элементов (объектов) системы различными способами резервирования, руководствуясь не только задачами надежности, но и экономическими задачами. Этот способ резервирования проанализируем на конкретном примере. Пусть задана схема (система) электроснабжения потребителя (см. рис. 6.15), собранная по основной схеме (одноцепная схема электроснабжения).
Такая система не обеспечивает требуемого уровня надежности электроснабжения потребителя за заданное время t. По одному из вариантов повышения надежности предлагается повысить надежность системы поблочно: в блоке кабелей используется нагруженное дублирование, на трансформаторной подстанции - дублирование замещением (см. рис. 6.16) в блоке ВЛ - нагруженное дублирование. Предполагается, что надежность выключателей значительно выше ВЛ, кабелей и трансформаторов. Принимаем вероятность безотказной работы выключателей равной единице. Резервирование ВЛ выполнено элементами λ2Л и λ2П с разными показателями. Требуется составить расчетное выражение по оценке надежности системы электроснабжения.
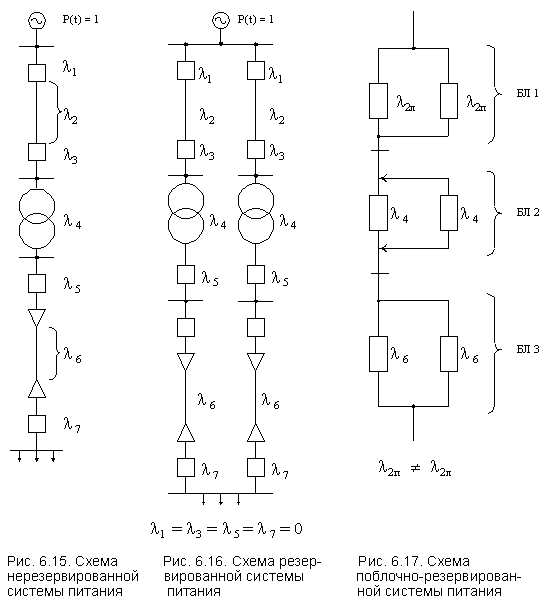
Сформулируем понятие отказа. Данная система будет работоспособна, если совпадут работоспособные состояния всех трех блоков: ВЛ, трансформаторной подстанции и блока кабелей. Расчетная схема представлена на рис. 6.17. Следовательно, вероятность безотказной работы этой системы
Где
; 
.
Поскольку в блоке 1 ВЛЛ и ВЛП имеют разные характеристики надежности, то вероятность безотказной работы этого блока по стандартной формуле (6.13) определять нельзя. Следует воспользоваться другими формулами. Блок 1 откажет, если совпадут отказы обоих цепей:
,
следовательно
.
Таким образом,
,
а средняя наработка до отказа
.