
Электротехника / Електротехніка
.pdf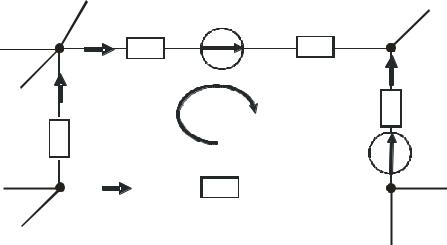
|
R2 |
E2 |
R3 |
a |
|
||
I2 |
|
b |
|
|
|
|
|
I1 |
|
|
I4 |
|
|
|
|
|
|
|
R4 |
R1 |
|
|
E4 |
|
|
R5 |
|
|
I5 |
|
|
|
|
|
|
d |
|
|
c |
|
|
|
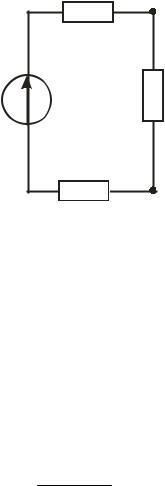
Рисунок 1.10 – Контур розгалуженого електричного кола
1.6 Методи розрахунків електричних кіл
Загальна задача аналізу електричного кола полягає в тому, що за ві- домою схемою кола з наперед заданими параметрами (ЕРС і опорами) не- обхідно розрахувати струми, потужності і напруги на окремих ділянках.
Розв'язання задач аналізу базується на законах Ома і Кірхгофа. Закон Ома застосовується головним чином при розрахунках режимів роботи окремих ділянок кола, а закони Кірхгофа – при розрахунках більш склад- них електричних кіл.
Необхідно пам'ятати, що нерозгалужене електричне коло характери- зується тим, що на всіх його ділянках протікає той самий струм, а розгалу- жене містить одну чи декілька вузлових точок, при цьому на окремих ділян- ках кола можуть протікати різні струми.
1.6.1 Метод еквівалентних перетворень (метод трансфігурацій)
Розрахунок електричних кіл із одним джерелом енергії можна про- водити за допомогою методу еквівалентних перетворень. Зазначений метод полягає в тому, що електричні кола заміняються більш простими за структурою ділянками, при цьому струми й напруги на неперетвореній частині кола не повинні змінюватися. У результаті перетворення структура кола і його розрахунок значно спрощуються.
При послідовному з'єднанні елементів (у нерозгалуженому колі) (рис. 1.11, а) до одного з виводів попереднього елемента приєднується один із виводів наступного так, що після всіх з'єднань утворюється ділянка
21
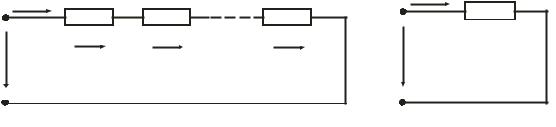
з двома виводами (рис. 1.11, б). |
|
|
Rекв |
||
I |
R1 |
R2 |
Rn |
I |
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
U1 |
U2 |
Un |
|
|
U |
|
|
|
U |
|
- |
|
а) |
|
- |
б) |
|
|
|
|
||
Рисунок 1.11 – Еквівалентне перетворення нерозгалуженого
електричного кола
Струм І, що протікає в усіх послідовно з'єднаних елементах, один і той самий, напруга U на кінцевих виводах кола дорівнює сумі спаду напруг на кожному з його елементів:
I = I1 = I2 K = In ,
U = U1 + U2 +K + Un = I R1 + I R 2 +K + I R n = I (R1 + R 2 +K + R n ) .
Таким чином, електричне коло з послідовним з'єднанням n опорів замінюється на коло з одним еквівалентним опором (рис. 1.11, б), значення якого дорівнює
R екв = R1 + R 2 +K + R n . |
(1.9) |
Тобто еквівалентний опір послідовного з'єднання дорівнює сумі опо- рів послідовно з'єднаних опорів (резистивних елементів).
Паралельне з'єднання (рис. 12, а) характеризується тим, що всі еле- менти приєднуються до однієї і тієї самої пари вузлів електричного кола. При цьому до всіх елементів прикладена одна й та сама напруга U, а зага- льний струм І дорівнює
U = U1 = U2 K = Un ,
I = I + I |
2 |
+K + I |
n |
= |
U |
+ |
U |
+K |
U |
= U ( |
1 |
+ |
1 |
+K |
1 |
) . |
|
|
|
|
|
|
|||||||||||
1 |
|
|
R1 |
|
R 2 |
|
R n |
|
R1 R 2 |
|
R n |
|||||
|
|
|
|
|
|
|
|
|
||||||||
Таким чином, електричне коло з паралельним з'єднанням n опорів замінюється на коло з одним еквівалентним опором (рис. 1.12, б), значення якого Rекв визначається за формулою
1 |
= |
1 |
+ |
1 |
+K |
1 |
. |
(1.10) |
R екв |
|
R 2 |
|
|||||
|
R1 |
|
R n |
|
||||
22

+ |
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
I |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
U |
I1 |
|
|
R1 I2 |
|
R2 In |
|
|
Rn |
|
U |
|
|
Rекв |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
а) |
|
|
|
|
|
|
б) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рисунок 1.12 – Еквівалентне перетворення розгалуженого електричного кола з паралельним з’єднанням елементів
У разі паралельного з'єднання двох опорів еквівалентний опір дорівнює
R екв = |
R1 R 2 |
|
. |
(1.11) |
|
R1 + R |
2 |
||||
|
|
|
Еквівалентний опір ділянки кола, яка складається з n однакових паралельно з'єднаних опорів, визначається як
R
R екв = n .
У складних колах зустрічаються з'єднання, які не можна віднести ні до послідовних, ні до паралельних. Такими є трипроменева зірка (рис. 1.13, а) та трикутник опорів (рис. 1.13, б). Їх взаємне еквівалентне пе- ретворення в багатьох випадках дозволяє істотно спростити схему й при- вести її до змішаного з'єднання опорів.
|
|
a |
a |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
R3 |
|
|
|
|
R13 |
|
|
|
R12 |
||
|
|
|
||||||||||
|
|
R2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
c |
|
|
|
c |
|
|
R23 |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
а) |
|
б) |
||||||||
а – трипроменевою зіркою; б – трикутником Рисунок 1.13 – З’єднання опорів
23

Зазначені заміни трикутника й зірки опорів повинні бути еквіва- лентними, тобто при відповідно незмінних напругах між вузлами a, b, c трикутника й зірки струми в зовнішній частині кола також повинні за- лишатися без змін.
Опори еквівалентного трикутника (заміна зірки на трикутник) визна- чаються за формулами:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
R12 = |
R1 R 2 |
+ R1 + R 2 , |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 2 R 3 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
R13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R12 |
|
R 23 = |
|
+ R 2 |
+ R 3 |
, |
(1.12) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
R13 = |
|
R1 R 3 |
+ R1 |
+ R 3 . |
|
|
||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
R 2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким чином, для визначення опору сторони еквівалентного трикут- ника підсумовують опори двох віток зірки, приєднаних до тих самих вузлів, що й сторона трикутника, та їх добуток, поділений на опір тре- тьої вітки зірки.
Якщо зіркою з’єднані три однакові опори R, тоді кожен з опорів ек- вівалентного трикутника згідно з формулою (1.12) буде дорівнювати 3R.
Опори еквівалентної зірки (заміна трикутника на зірку) визначаються за формулами:
|
|
|
a |
R1 |
|
|
|
|
R13 |
R12 |
, |
|
|
|||
|
|
|
|
|
= |
|
|
|
|
|||||||
|
|
|
|
|
R13 + R12 + R 23 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
R1 |
R 2 |
= |
|
R12 R 23 |
|
|
|
, |
(1.13) |
||||||
R13 |
|
|
|
R12 |
|
|
|
|
||||||||
|
|
|
|
R13 + R12 + R 23 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
R 3 |
|
= |
|
|
R13 |
R 23 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
R3 |
|
|
|
R2 |
|
|
R13 + R12 + R 23 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
c |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
R23 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отже, опір вітки еквівалентної зірки дорівнює добутку опорів двох сторін трикутника, які приєднані до тієї самої вершини, що й вітка зірки, поділеному на суму опорів усіх сторін трикутника.
Якщо трикутником з’єднані три однакові опори R, тоді кожен з опо- рів еквівалентної зірки згідно з формулою (1.13) буде дорівнювати R3 .
24
Приклад 1.1
Знайти: 1) струм у нерозгалуженій ділянці складного електричного кола з одним джерелом живлення (рис. 1.14); 2) струми та спад напруги на кожному окремому елементі; 3) перевірити баланс потужностей. Зна- чення ЕРС, внутрішнього опору ЕРС і опорів зовнішньої частини кола вважаються відомими.
|
|
|
R1 |
|
|
|
|
|
b |
|
R |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R5 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
E, R0 |
|
|
|
|
R2 |
|
|
|
|
|
|
d |
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
c |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
R8 |
|
|
|
|
R6 |
|
|
|
R |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.14 – Складне електричне коло з одним джерелом ЕРС
Розв'язання
Оскільки задане коло має одне джерело живлення, для розв’язання задачі застосуємо метод еквівалентних перетворень.
Проведемо заміну трикутника опорів R3, R4, R5 на еквівалентну три- променеву зірку з опорами R34, R45, R35, зовнішні виводи («проміні») якої підімкнені до тих самих точок b, c, d кола, у яких знаходилися вершини
трикутника (порівняйте рисунки 1.15 і 1.16). |
|
|
|
|
|
|
||||||||
|
|
|
R1 |
|
|
g |
b |
|
|
|
|
|||
|
|
|
|
|
|
|
R4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E, R0 |
|
|
|
|
|
|
c |
|
|
|
R5 |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
R8 |
|
|
|
|
R6 |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
f |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Рисунок 1.15 – Заміна «трикутника» на еквівалентну «зірку»
Перетворена еквівалентна схему набуває значно простішого вигляду та містить тільки послідовно та паралельно з’єднані елементи (рис. 1.16). Слід зазначити, що вузли b, c, d кола перетворюються в точки.
25

|
|
|
R1 |
|
|
g |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
R34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R45 |
|
d |
|
|
|
|
|
R2 |
|
|
e |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
E, R0 |
|
|
|
|
|
R35 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
R8 |
|
|
|
|
R6 |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
f |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
Рисунок 1.16 – Електрична схема після заміни опорів, з’єднаних «трикутником» на еквівалентну трипроменеву «зірку»
Значення опорів R34, R45, R35 визначають відповідно до формул (2.13):
R 34 |
= |
|
|
R 3 |
R 4 |
, |
||
|
R 3 |
+ R 4 |
+ R 5 |
|||||
|
|
|
|
|
||||
R 45 |
= |
|
|
R 4 |
R 5 |
|
, |
|
|
R 3 |
+ R 4 |
+ R 5 |
|
||||
|
|
|
|
|
||||
R 35 |
= |
|
|
R 3 |
R 5 |
. |
||
|
R 3 |
+ R 4 |
+ R 5 |
|||||
|
|
|
|
|
||||
Наступним кроком є заміна послідовно з’єднаних опорів R45 і R7, R35 і R6 їх відповідними еквівалентами – R457, R356 , опори яких розраховують згідно з формулою (1.9):
R 457 = R 45 + R 7 , R 356 = R 35 + R 6 .
Після зазначеного перетворення схема набуває вигляду, який наве- дено на рисунку 1.17.
Як можна бачити, опори R457 і R356 з’єднані паралельно. Їх еквівален- тний опір R/, який з’єднується з вузлами e та f, може бути знайдений за фор-
мулою (1.11):
R′ = R 457 R 356
R 457 + R 356 .
Після цього перетворення схема набуває вигляду, наведеного на рисунку 1.18.
26
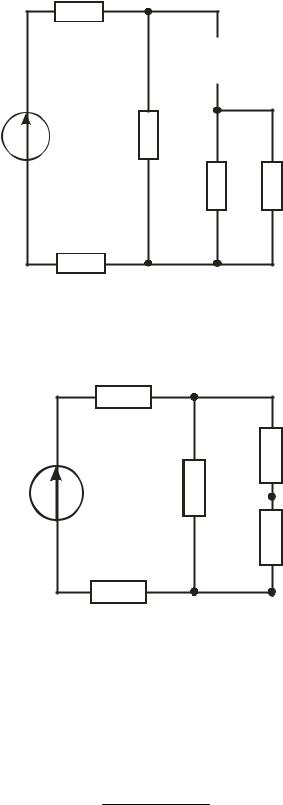
R1 g
R34 
E, R0 |
|
R2 |
|
e |
|
|
|||
|
|
|
R356 |
R |
|
457 |
R8
h f
Рисунок 1.17 – Електрична схема після заміни опорів R45 і R7, R35 і R6
відповідними еквівалентними опорами R457, R356
R1 |
|
g |
|
|
R34 |
E, R0 |
R2 |
e |
|
||
|
|
R/ |
R8 |
|
f |
|
|
|
|
|
h |
Рисунок 1.18 – Електрична схема після заміни опорів R457 і R356
на еквівалентний опір R/
Видно, що опір R2 з’єднаний паралельно з послідовно з’єднаними опорами R34 і R/. Їх об’єднаний еквівалентний опір R//, який після пере- творення схеми з’єднується з точками g і h схеми, визначається так:
R // = R 2 (R 34 + R / ) .
R 2 + R 34 + R /
Після цього перетворення схема набуває вигляду, наведеного на рисунку 1.19.
27
R1 |
g |
E, R |
R// |
0 |
|
R8 |
|
|
h |
Рисунок 1.19 – Електрична схема після заміни опорів R2, R34 та R/
еквівалентним опором R//
Усі опори у даному електричному колі з’єднані послідовно. Еквіва- лентний опір зовнішньої частини кола дорівнює
R екв = R1 + R // + R8 .
Струм І у нерозгалуженій ділянці кола може бути знайдений відпові- дно за формулою (1.3):
E
I = R 0 + R екв .
Як можна побачити з електричної схеми (рис. 1.19), струм І у нероз- галуженій ділянці кола дорівнює струмам опорів R1, R8 і R//, оскільки в цьому разі маємо просте або нерозгалужене коло. Спад напруги на цих опорах знаходять відповідно до закону Ома (формула (1.2.1) для визначен- ня напруги). Таким чином,
I = I, |
I |
8 |
= I, I// |
= I, |
U |
1 |
= IR |
1 |
, |
U |
8 |
= IR |
8 |
, U // |
= IR // . |
1 |
|
|
|
|
|
|
|
|
|
|
Для подальшого знаходження струмів і спадів напруги переходимо до розгляду схеми на рисунку 1.18, взявши до уваги, що різниця потенціа- лів між точками g та h дорівнює U//.
Відповідно до цього визначимо: 1) струм І2 опору R2; 2) струм І34 по- слідовно з’єднаних опорів R2 та R/; 3) спад напруги на опорах R2, R34 та R/:
I2 |
= |
U // |
, I34 = I/ = |
U // |
, U2 = U // , U34 = I34 R 34 , U / = I/ R / . |
|
R 2 |
R 34 + R / |
|||||
|
|
|
|
28
Взявши до уваги, що різниця потенціалів між точками е та f дорівнює U/, переходимо до розгляду схеми на рисунку 1.17.
Визначимо струми І356 і І457 опорів R356, R457, які з’єднані паралельно:
|
U / |
U / |
||
I356 = |
|
, I457 = |
|
. |
|
|
|||
|
R 356 |
R 457 |
||
Далі переходимо до розгляду схеми на рисунку 1.16.
Опори R35 і R6 з’єднані послідовно, тому струм І6 опору R6 і струм І35 опору R35 дорівнюють відповідно струму І356, спад напруги на опорах R35 і R6 знайдемо за законом Ома:
I6 = I356 , I35 = I356 , U6 = I6 R 6 , U35 = I35R 35 .
Опори R45 і R7 також з’єднані послідовно, тому струм І7 опору R7
і струм І45 опору R45 дорівнюють |
відповідно |
струму І457, спад напруги |
на опорах R45 і R7 знайдемо за законом Ома: |
|
|
I7 = I457 , I45 = I457 , |
U7 = I7 R 7 , |
U45 = I45R 45 . |
Решту невідомих струмів і відповідних спадів напруги знайдемо за допомогою першого та другого законів Кірхгофа. Для цього повернемо- ся до початкової схеми, на якій довільно позначимо напрями струмів у вітках (рис. 1.20).
|
|
|
R1 |
|
|
b |
|
|
R4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
|
|
I3 |
|
I4 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
E, R0 |
|
|
|
|
R2 |
|
|
|
|
|
|
R5 |
|
|
d |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R6 |
|
|
|
I6 |
|
I5 |
I7 |
|
|
|||
|
|
|
R8 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R7 |
|
|
|
||
Рисунок 1.20 – Складне електричне коло з одним джерелом ЕРС
Визначимо напругу U5, для чого, вибравши напрямок обходу проти руху годинникової стрілки, запишемо другий закон Кірхгофа для контуру, що складається з опорів R5, R7 і R6:
U5 + U6 − U7 = 0 U5 = −U6 + U7 .
29

Тоді струм І5 опору R5 дорівнює
I5 = U5 .
R 5
Невідомі струми І3 та І4 можна легко знайти за допомогою першого закону Кірхгофа для вузлів с і d схеми (рис. 1.20), після чого визначити відповідні спади напруги:
I3 + I5 − I6 = 0 I3 = −I5 + I6 ,
U3 = I3R3 ,
I4 − I5 − I7 = 0 I4 = I5 + I7 ,
U4 = I4R 4 .
Таким чином, усі невідомі струми та відповідні спади напруги визначені.
Для перевірки знайдених значень перевіримо баланс потужності, для чого визначимо потужність Рдж, яку віддає джерело живлення у зовнішнє коло, та сумарну потужність Рпр приймачів електричної енергії:
Pдж = (E − I R 0 ) I,
Pпр = I12 R1 + I2 2 R 2 + I3 2 R 3 + I4 2 R 4 + I5 2 R 5 + I6 2 R 6 + I7 2 R 7 + I8 2 R 8 .
Якщо Pдж = Pпр , це означає, що задачу розв’язано вірно.
1.6.2 Метод безпосереднього застосування законів Кірхгофа
Закони Кірхгофа є найбільш загальними, універсальними законами, які описують режим роботи електричного кола. Методи розрахунку, які засновані на цих законах, можуть бути застосовані до розрахунку будь-яких електричних кіл. Найчастіше їх застосовують для визначення струмів у вітках складних кіл із декількома джерелами електричної енергії.
Для того щоб визначити режим роботи електричного кола за допомогою методу безпосереднього застосування законів Кірхгофа, необхідно:
1) для вузлів схеми скласти незалежні рівняння відповідно до першого закону Кірхгофа;
2) для незалежних контурів схеми скласти рівняння відповідно до другого закону Кірхгофа;
3) вирішити складену систему рівнянь і розрахувати струми в кожній вітці кола. Для перевірки правильності розв'язання скласти баланс потужностей.
30
