2.1.14 Построение лекальной кривой подбором дуг
Любая лекальная кривая может быть вычерчена циркулем путем подбора центров, из которых описываются дуги, совпадающие с отдельными участками кривой. Для того чтобы описываемые дуги плавно переходили одна в другую, необходимо, чтобы точки их сопряжения (касания) лежали на прямых, соединяющих центры. Построение ведут в следующем порядке: подобрав центр 1 для какого-либо участка кривой аb, подбирают центр 2 для следующего участка bс на продолжении радиуса, проходящего через точки b и 1; для участка сd подбирают центр 3 на продолжении радиуса, проходящего через точки с и 2, и т. д. Таким образом можно обвести всю кривую, не меняя лекала (рис. 2.19).
Рисунок 2.19
2.1.15 Сопряжение двух параллельных прямых двумя дугами
Заданные на прямых точки А и В соединяются отрезком АВ, на котором отмечают произвольную точку М. В середине отрезков АМ и ВМ проводят к ним перпендикуляры; в точках А и В также восстанавливают перпендикуляры к данным прямым. На пересечении соответствующих перпендикуляров находятся центры О1 и О2. Радиусы закругления: R1 = О1В; R2 = О2В. Касание дуг происходит в точке М, находящейся на линии центров О1О2. Если точку М выбрать на середине линии АВ, то R1 = R2 (рис. 2.20).
Рисунок 2.20
2.2 Деление окружности на равные части и построение правильных вписанных многоугольников
2.2.1 Деление окружности на четыре равные части и построение правильного вписанного четырехугольника
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника можно выполнить циркулем и динейкой. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 2.21). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
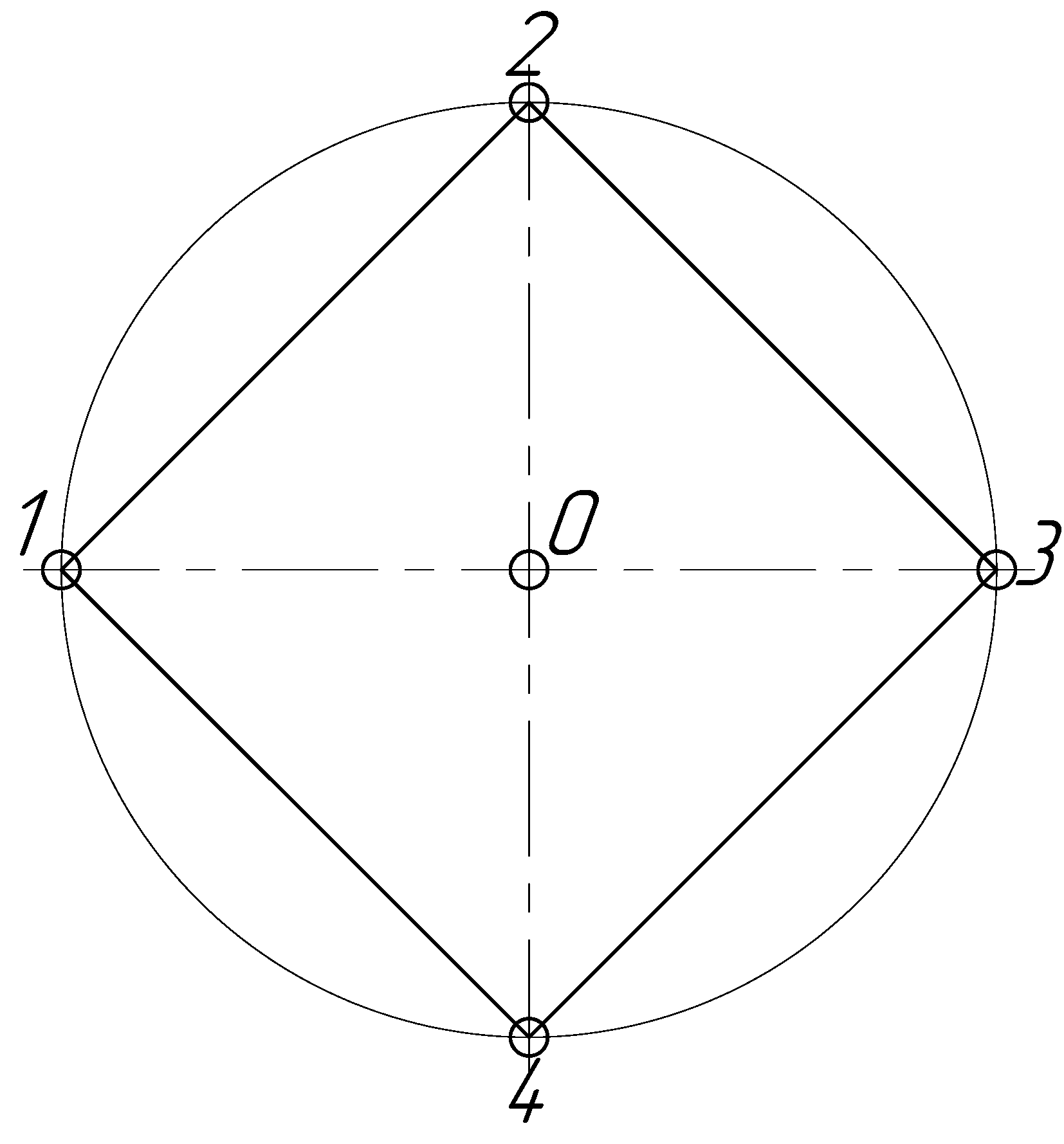
Рисунок 2.21
2.2.2 Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника
Две взаимно перпендикулярные линии, проведённые под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 90° (рис. 2.22), вместе с центровыми линиями разделят окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 2.22). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 2.22).
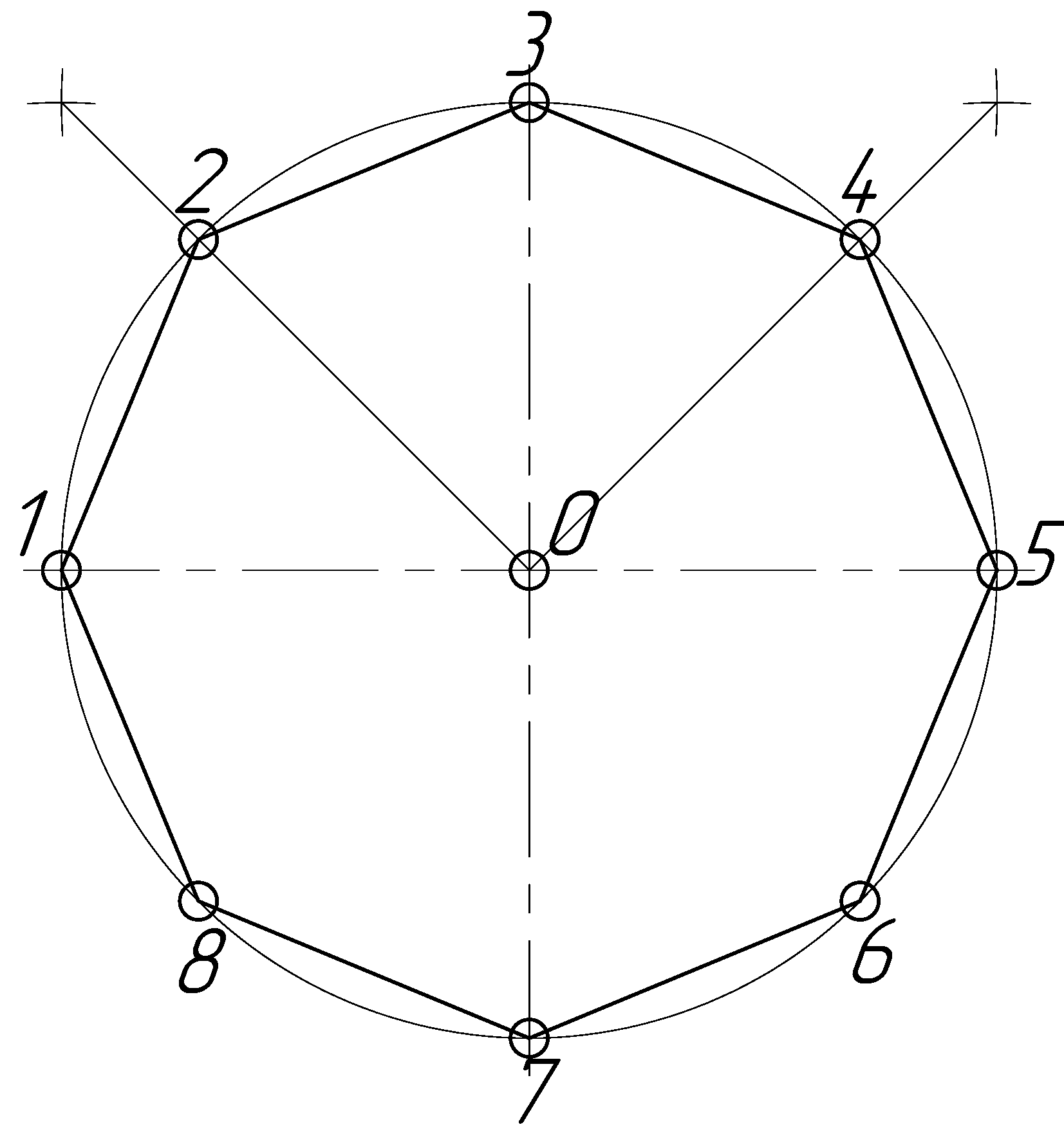
Рисунок 2.22
2.2.3 Деление окружности на три равные части и построение правильного вписанного треугольника
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля.
При делении окружности циркулем на три равные части из любой точки окружности, например из точки А пересечения центровых линий с окружностью (рис. 2.23, а), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку А. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 2.23, б, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R, равным радиусу данной окружности, получают точки 2 и 3. При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 2.23, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 2.23 в).
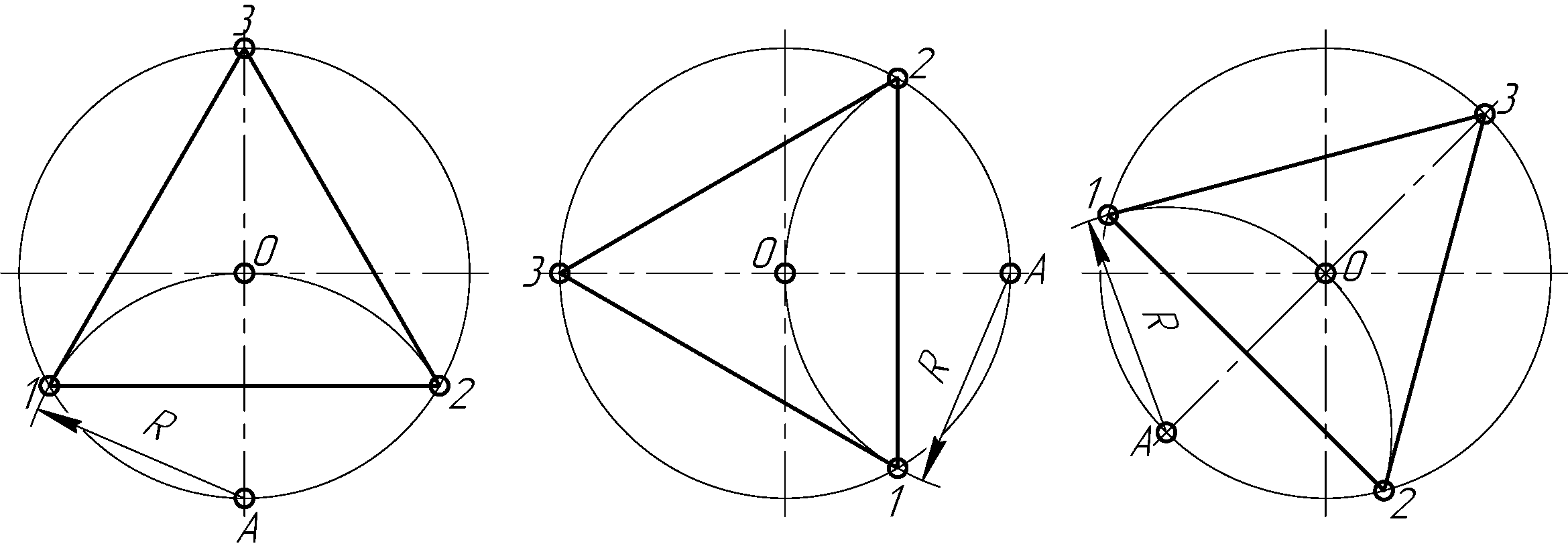
а) б) в)
Рисунок 2.23