2.1.9 Построение общей касательной к двум данным окружностям радиусов r1 и r2

Из средней точки прямой ОО₁ через центр О₁ строится вспомогательная окружность. Из центра большой окружности радиуса R₁ проводится вторая вспомогательная окружность радиусом R₁ – R₂. Точка пересечения этих окружностей В определяет направление радиуса О₁К₁, идущего в точку касания. Для получения точки касания К₂ на второй окружности достаточно провести из центра О₂ радиус О₂К₂ параллельно радиусу О₁К_1, остается соединить найденные точки касания прямой линией (рис. 2.11).

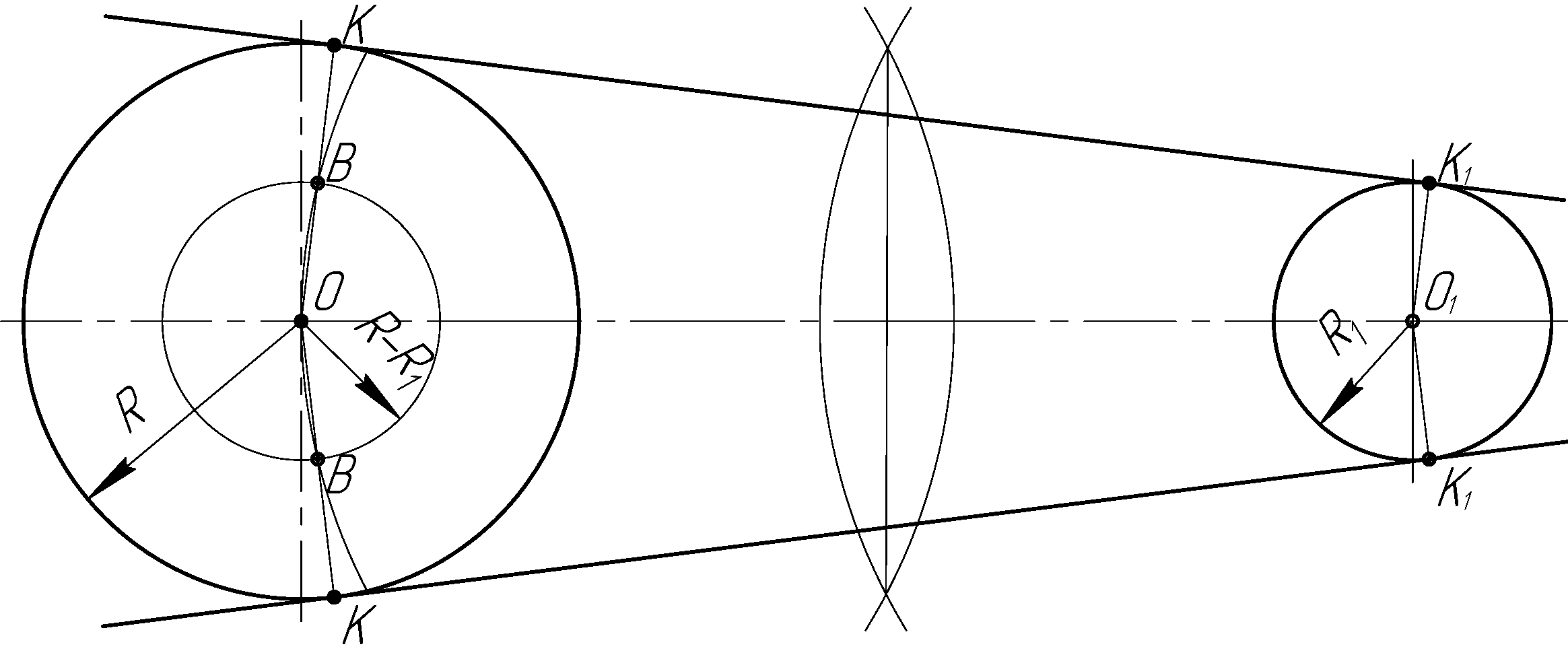
Рисунок 2.11

Касательные к данным окружностям можно провести так же, как показано на рис. 2.12. В этом случае из центра большой окружности проводят вспомогательную окружность радиусом равным сумме радиусов данных окружностей, т. е. R₁ + R₂.

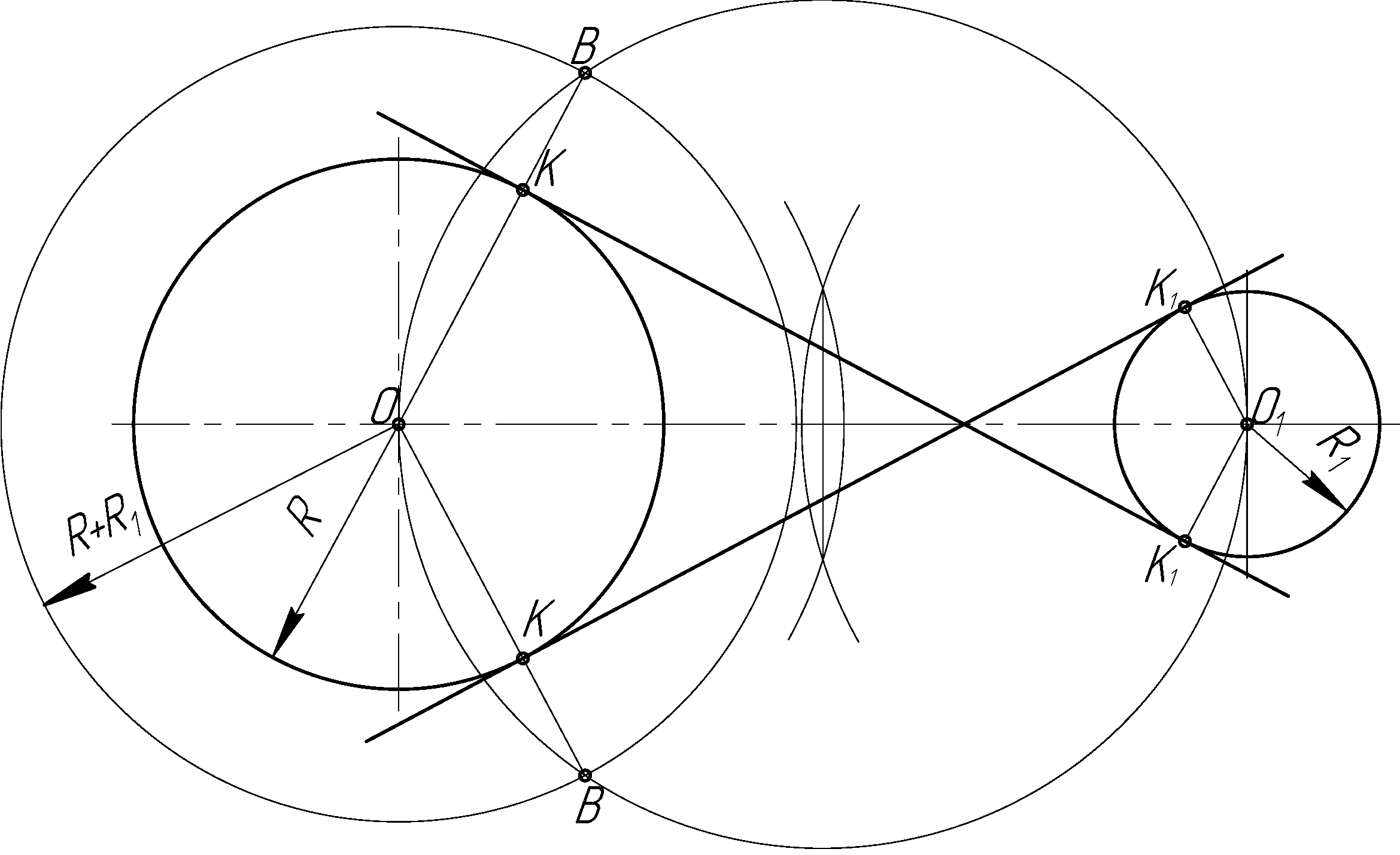
Рисунок 2.12

2.1.10 Построение окружности, проходящей через данную точку а и касающейся данной окружности (с центром о) в заданной точке в

Через середину прямой АВ проводят перпендикуляр, в точке пересечения которого с линией О В получают центр О искомой окружности; радиус её равен О₁В или О₁А (рис. 2.13 и 2.14).

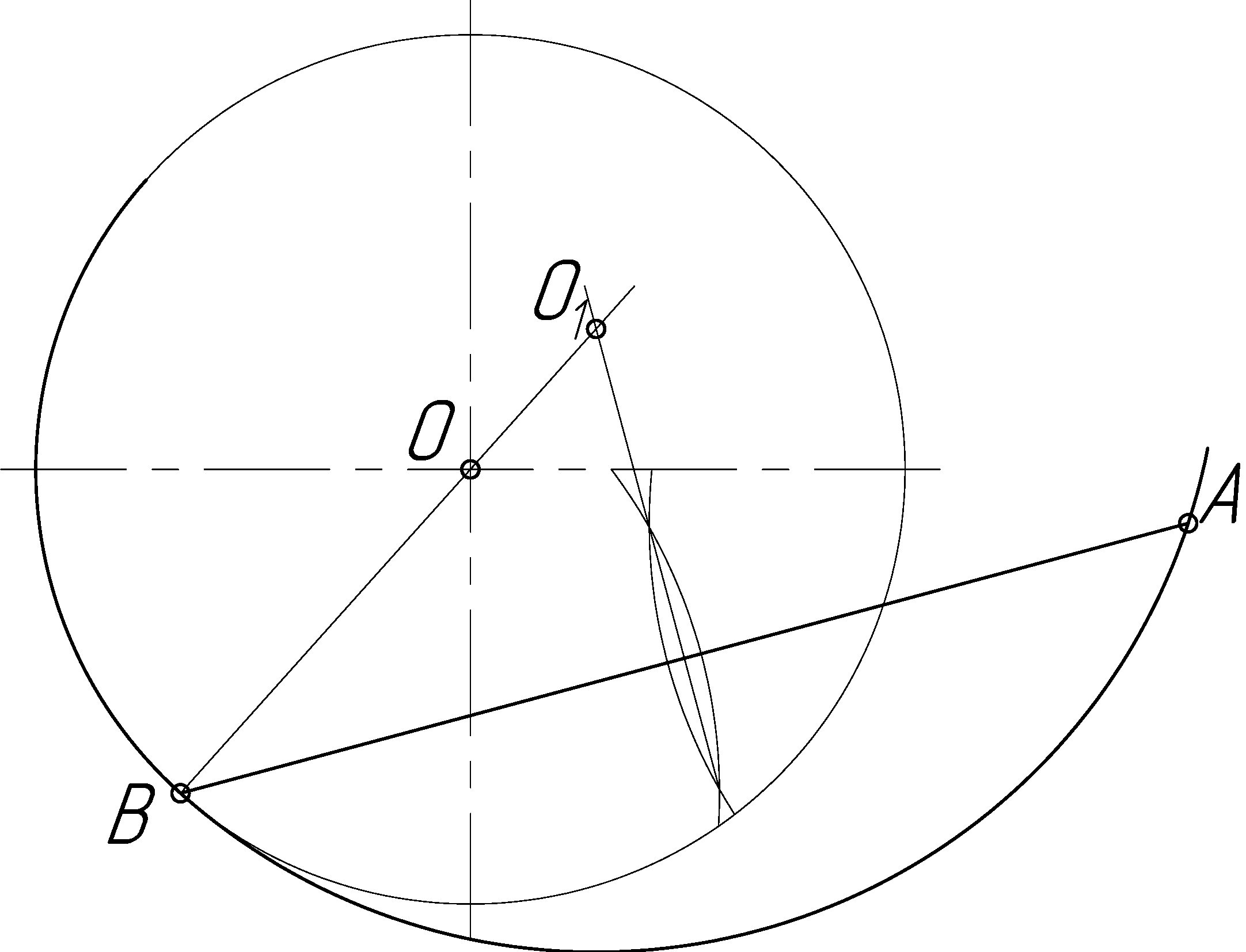
Рисунок 2.13

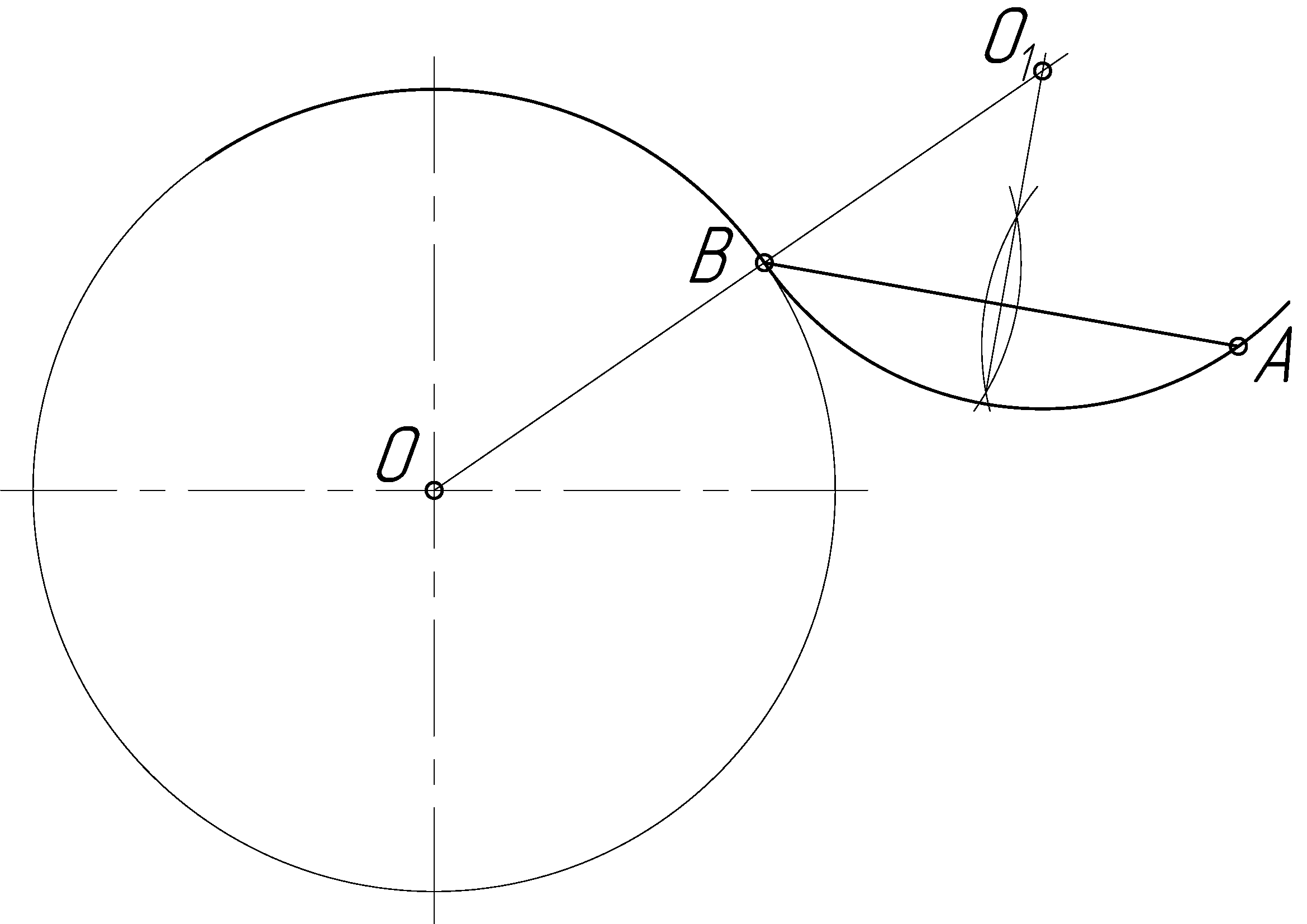
Рисунок 2.14

2.1.11 Сопряжение окружности и прямой при условии, что дуга сопряжения должка проходить через точку а на прямой

Из данной точки А на прямой LМ восстанавливается перпендикуляр к прямой LМ; на его продолжении откладывается отрезок АВ, равный радиусу R окружности (АВ = R) (рис. 2.15).

Полученная таким образом точка В соединяется с центром Если пересечение окружности О₁ из точки А проводится прямая АК, параллельная линии ВО₁; пересечение ее с окружностью определит точку касания К ис­комой дуги сопряжения с окружностью. Остаётся продолжить отрезки О₁К и АВ до их пересечения, чтобы найти центр О₂ дуги сопряжения, а следовательно, и её радиус. Если пересечение прямых О₁К и АВ получается под очень острым углом, то центр О₂ можно найти пересечением любой из них с перпендикуляром, проведенным через середину линии О₁В (так как треугольник О₂ВО₁ – равнобедренный).

Рисунок 2.15

2.1.12 Сопряжение окружности и прямой при условии, что дуга сопряжения должна проходить через заданную точку а на окружности

Через точку А на окружности проводится к последней касательная АВ; угол, образуемый этой касательной и прямой LМ, делится пополам. Пересечение биссектрисы угла АВМ с продолжением радиуса ОА определяет центр О₁ и радиус О₁А искомой дуги сопряжения. Точкой сопряжения является точка К (рис. 2.16, 2.17).

Рисунок 2.16 Рисунок 2.17

2.1.13 Сопряжение двух неконцентрических дуг окружностей дугой заданного радиуса

Даны две дуги, описанные из центров О₁и О₂ радиусами R₁ и R₂. Для сопряжения их дугой заданного радиуса R₃ проводят из тех же центров две вспомогательные дуги радиусами R₁ – R₃ и R₂ + Rз. Пересечение этих дуг определяет искомый центр О. Точки касания К₁ и К₂ находятся на линиях центров ОО₂ и О₁О (рис. 2.18).

Рисунок 2.18