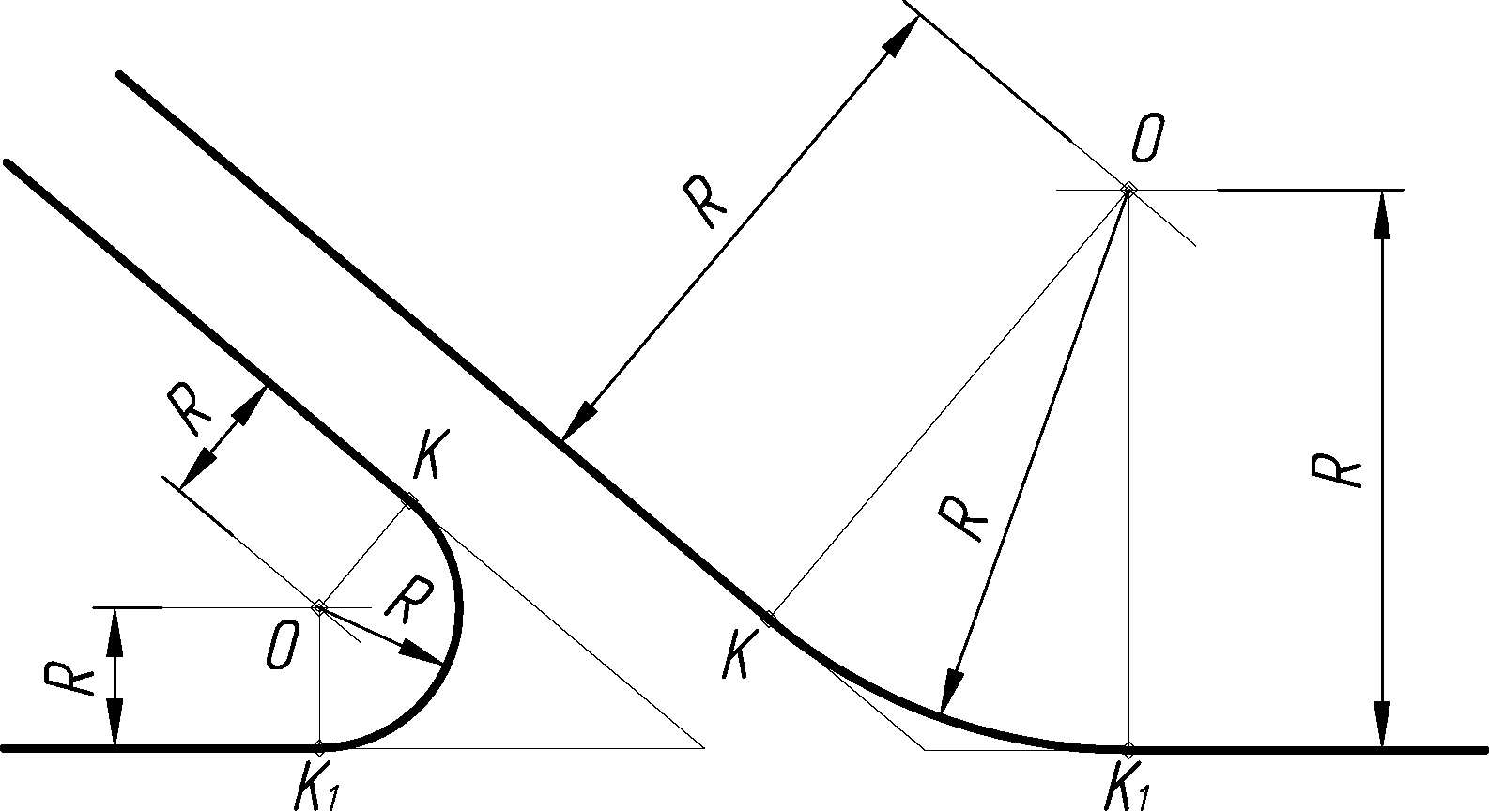
2.1.4 Сопряжение пересекающихся прямых дугой окружности данного радиуса

Построение сводится к проведению окружности, касающейся обеих данных прямых (рис. 2.5). Для нахождения центра этой окружности проводят вспомогательные прямые, параллельные данным, на расстоянии, равном радиусу R; точка пересечения этих прямых и будет центром О дуги сопряжения. Перпендикуляры, опущенные из центра О на данные прямые, определяют точки касания К и К₁ (рис. 2.5, а, б).

Рисунок 2.5

Этими точками и ограничивается дуга сопряжения. Если одна из точек касания, например К, является заданной, а радиус закругления не указан, то искомый центр О находится на пересечении перпендикуляра, проведенного из точки К, и биссектрисы угла, образуемого данными прямыми.

Если требуется провести окружность так, чтобы она касалась трех данных пересекающихся прямых АВ, ВС и СD, то в этом случае радиус не может быть задан наперед. Центр О искомой окружности находится в точке пересечения биссектрис углов В и С. Радиусом ее является перпендику­ляр, опущенный на любую из трех данных прямых (рис. 2.5, б).

2.1.5 Сопряжение данной окружности и данной прямой дугой заданного радиуса r

При внешнем касании (рис. 2.6) из центра О данной окружности радиусом R проводится дуга вспомогательной окружности радиусом R + R₁, а на расстоянии R – прямая, параллельная заданной. Точка пересечения проведенной прямой и дуги вспомогательной окружности определяет положение центра дуги сопряжения О₁. Соединяя найденный центр О₁ с центром О данной окружности и опуская из О₁ перпендикуляр на прямую, находят точки касания К и К₁, между которыми заключена дуга сопряжения. В случае внутреннего касания дуга вспомогательной окружности проводится радиусом R–R ₁ (рис. 2.7).

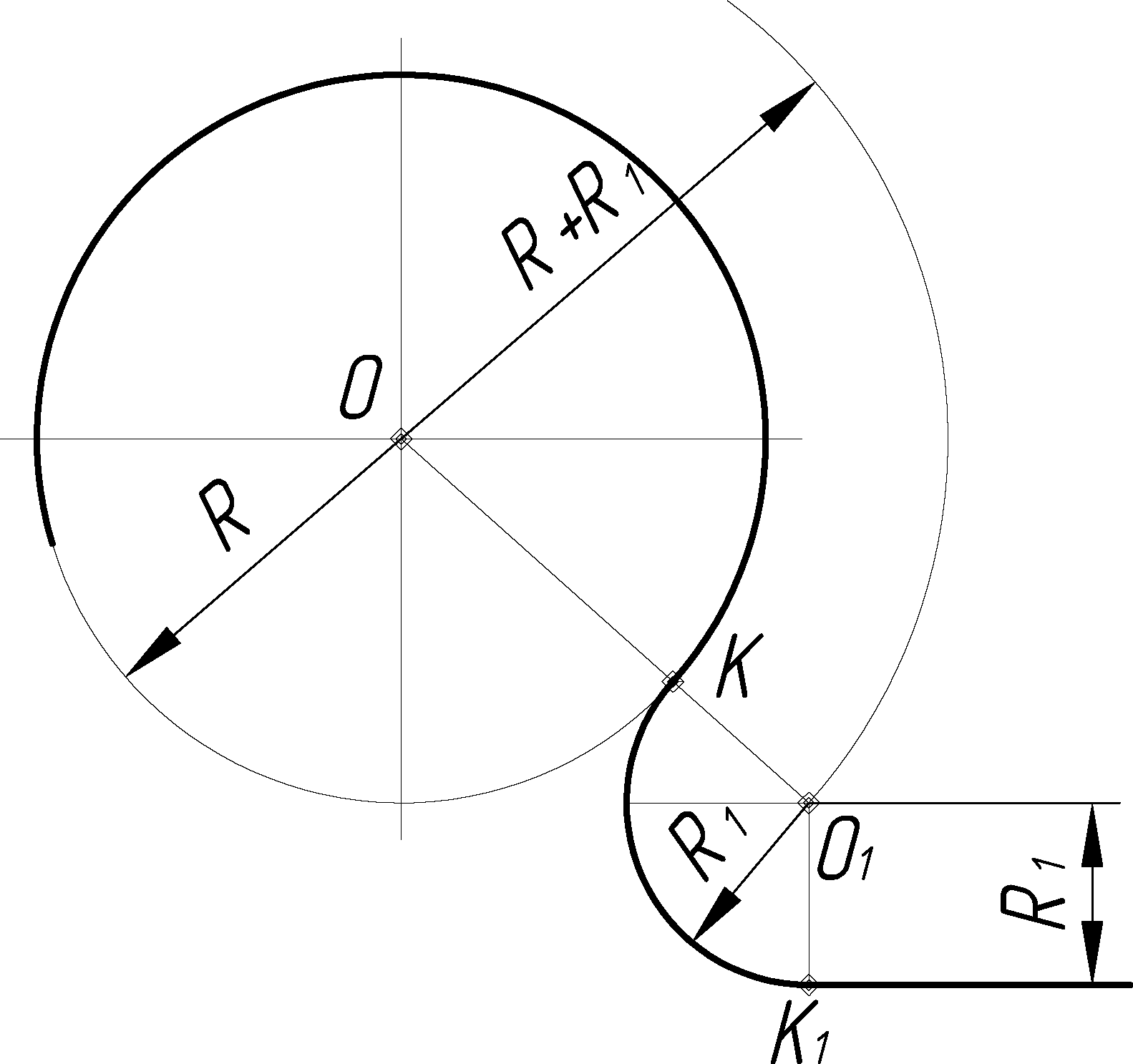
Рисунок 2.6

Рисунок 2.7

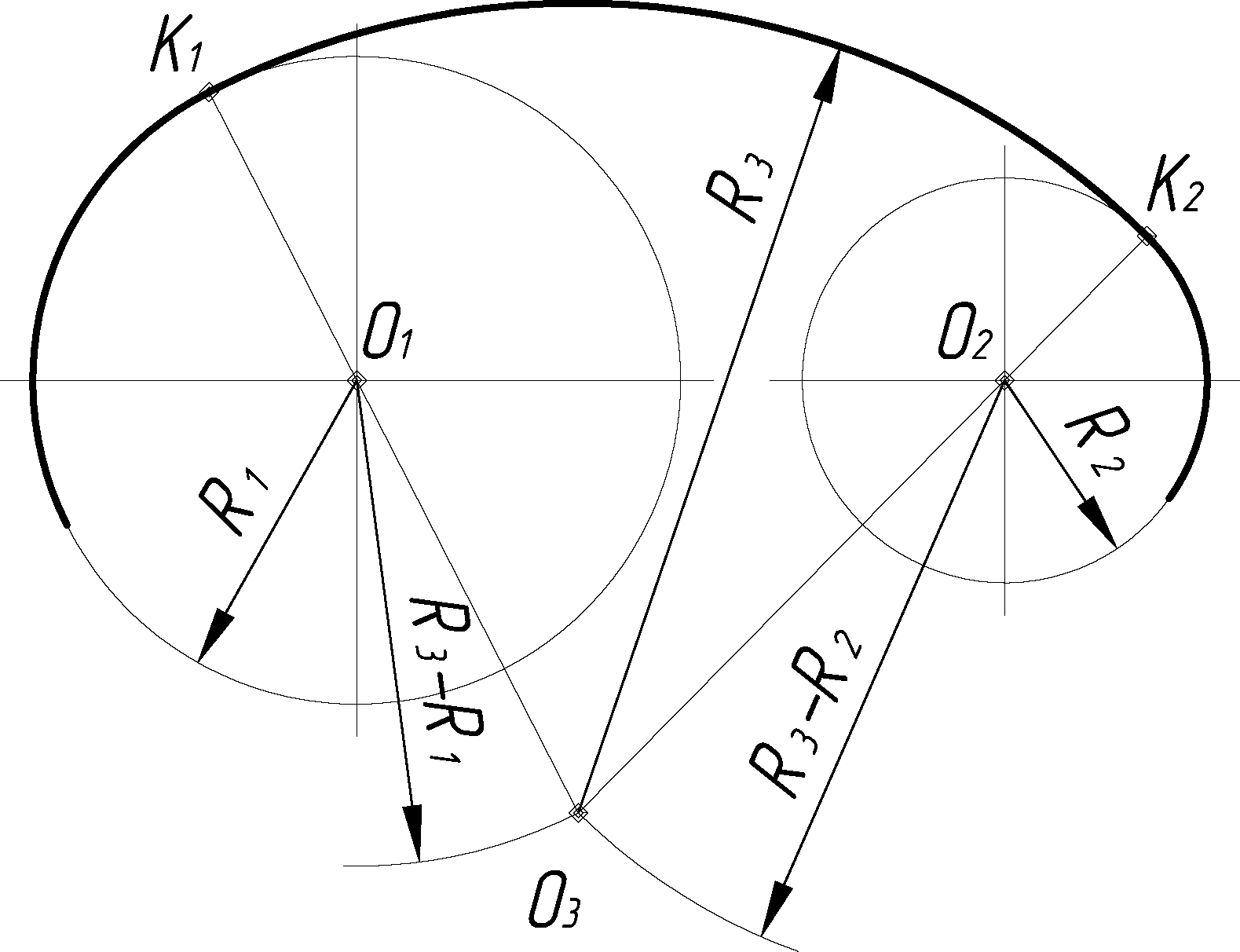
2.1.6 Сопряжение двух данных окружностей дугой заданного радиуса r3

При внешнем касании (рис. 2.8) из центра О₁ окружности радиусом R₁ описывается дуга вспомогательной окружности радиусом R₁+ R₃ и из центра О₂ окружности радиусом R₂ – дуга радиусом R₂ + R₃. Точка О₃ пересечения этих дуг является центром искомой дуги окружности радиусом R₃. Соединяя центры О₃ и О₁, а также О₃ и О₂, определяют точки касания К₁ и К₂.

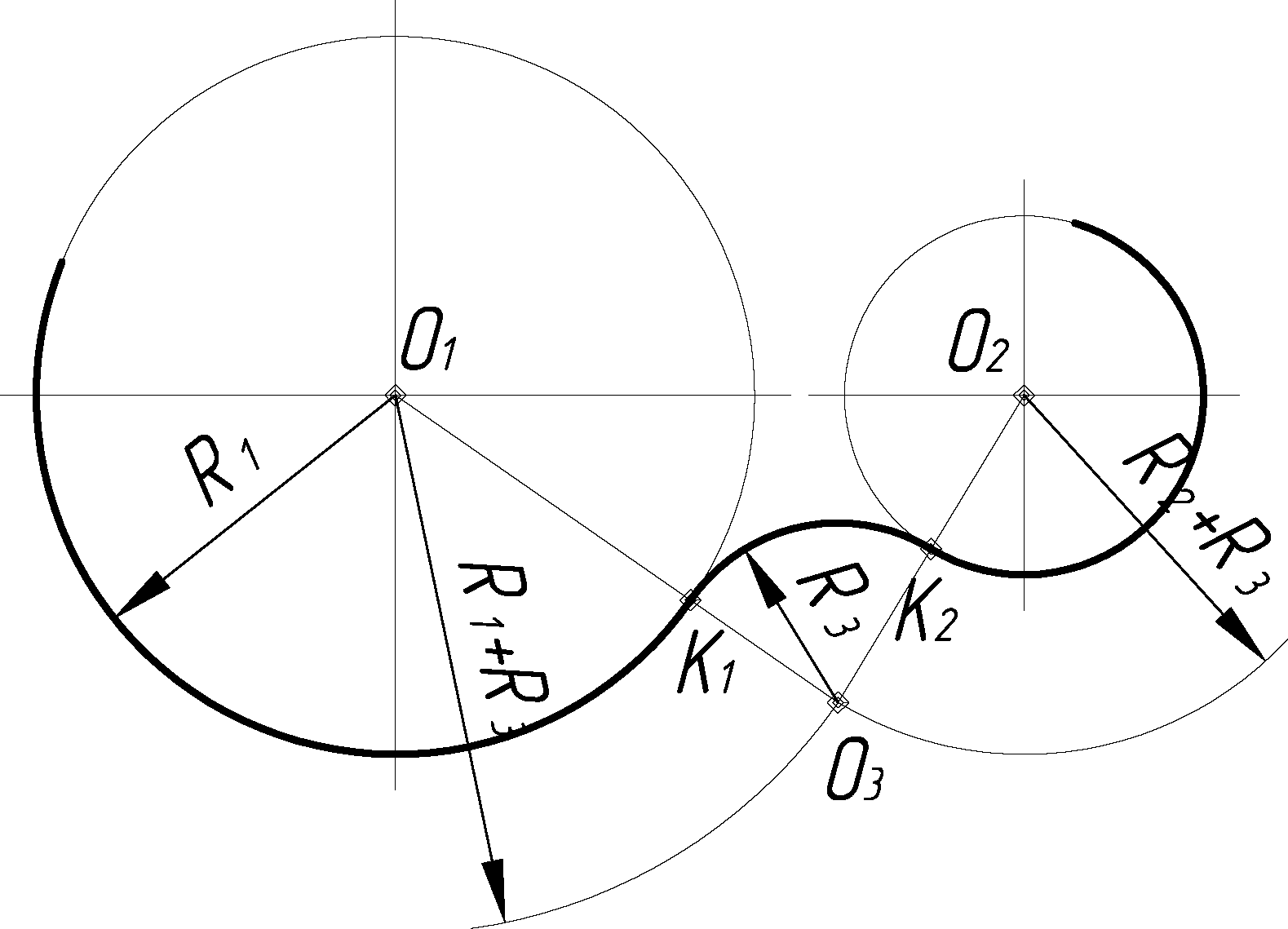
Рисунок 2.8

При внутреннем касании (рис. 2.9, а) вспомогательные дуги проводятся радиусами R₃–R₁, и R₃–R_2.

Рисунок 2.9

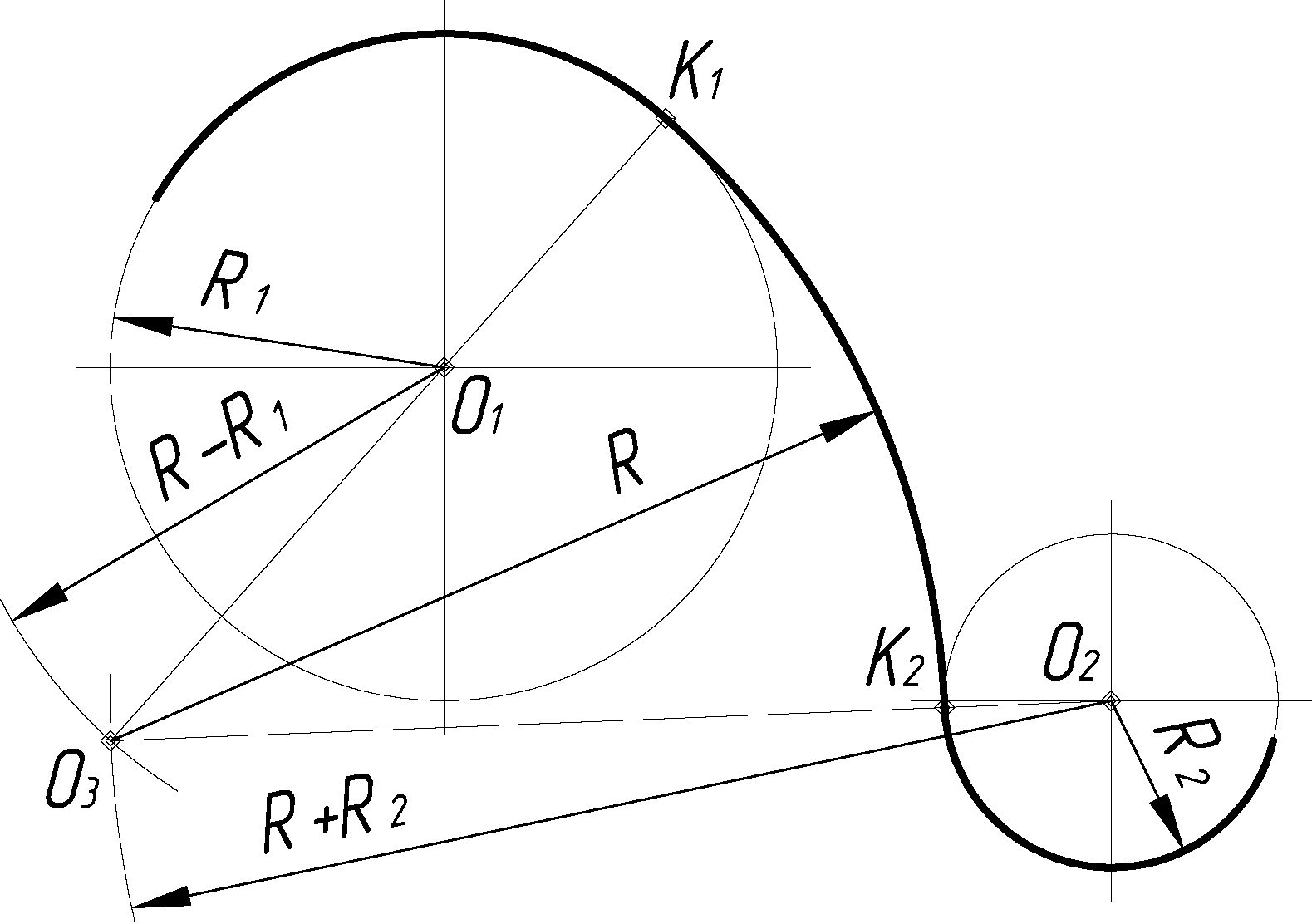
2.1.7 Случаи внешнего и внутреннего касания

Даны окружности радиусами r₁ и r₂ с центрами О₁ и О₂ (рис. 2.9, б). Требуется провести окружность данного радиуса R так, чтобы она имела с одной из данных окружностей внутреннее касание, а с другой – внешнее. Центр искомой дуги находится в точке пересечения двух дуг, описанных из центра О₁ радиусом R – r₁ и из центра О₂ – радиусом R + r₂; К и К₁ – точки касания.

2.1.8 Проведение касательной к окружности через заданную точку, лежащую вне окружности

Данную точку А соединяют с центром окружности О и из точки А через центр О очерчивают вспомогательную окружность. В точках пересе­чения вспомогательной и данной окружностей получают точки касания К и К₁; остаётся точку А соединить с этими точками (рис. 2.10).

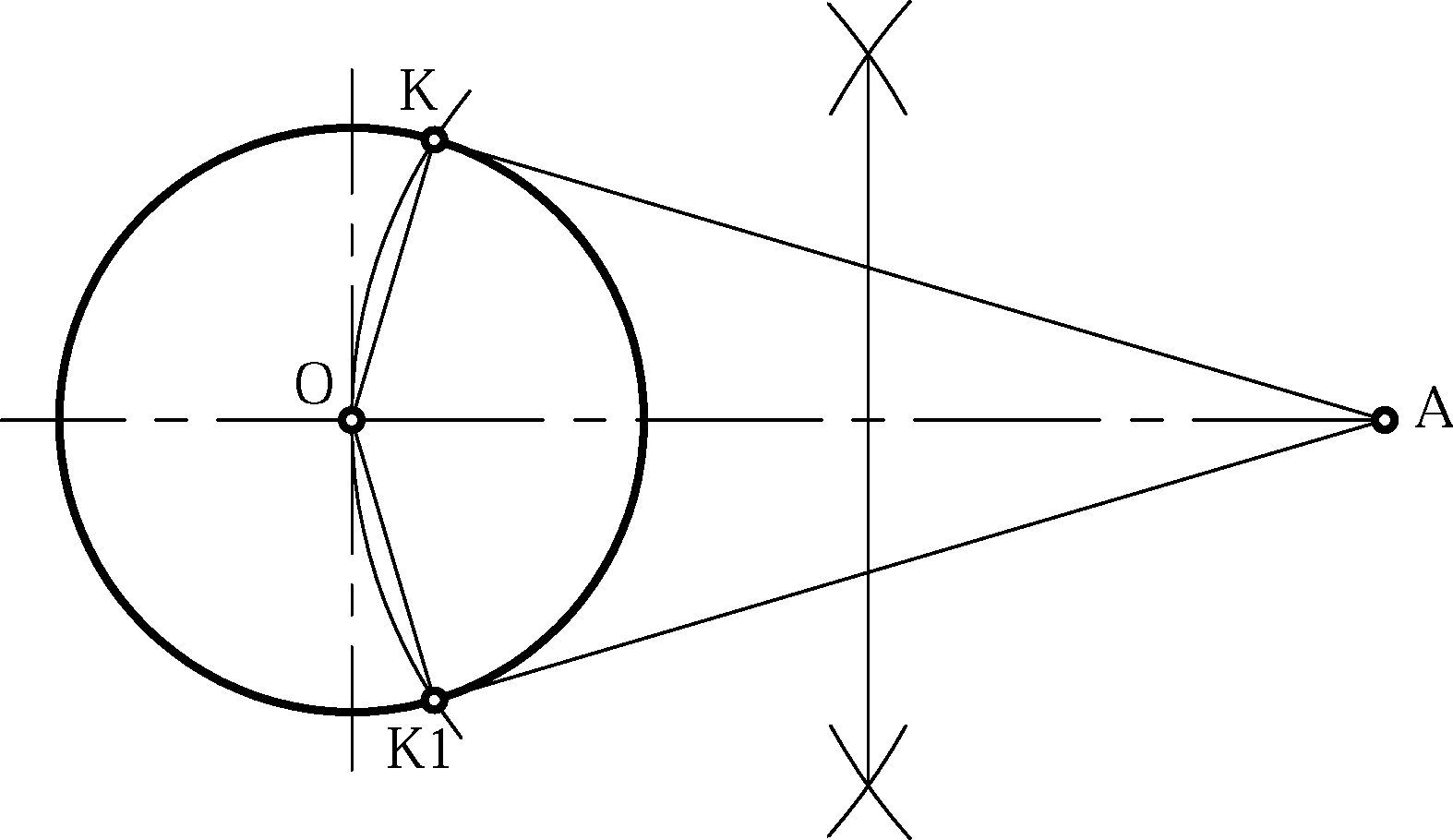
Рисунок 2.10