4.3 Проекция вектора на направление другого вектора

Рассмотрим два вектора и.

О

К

Отрезок ОК является проекцией вектора на направление вектора. Из полученного прямоугольного треугольника очевидно, что:

.

Из формулы (4.1) следует:

,

следовательно, можем записать:

.

Окончательно, проекция вектора на направление другого вектора вычисляется по формуле:

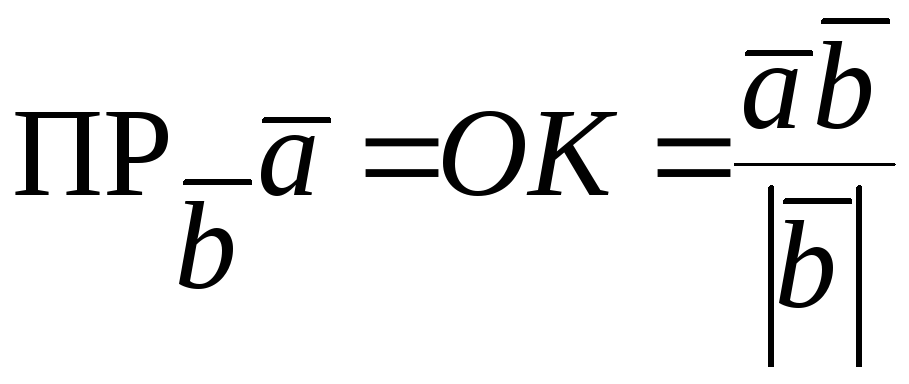(4.6)

ЛЕКЦИЯ 5

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

5.1 Определение векторного произведения

Векторным произведением двух векторов иназывается третийвектор , обладающий свойствами:

1. Вектор перпендикулярен плоскости, в которой расположены векторыи.

.

2. Длина вектора равна площади параллелограмма, построенного на векторахи, как на сторонах.

(5.1)

3. Векторы ,,, в том порядке, как они записаны, образуютправую тройку векторов.

Обозначения:

.

5.2 Вычисление векторного произведения двух векторов

Рассмотрим векторы: и. Векторное произведение этих векторов равноопределителю третьего порядка, элементами первой строки которого являются единичные орты , элементами второй и третьей строк – координаты векторовисоответственно.

(5.2)

Запишем разложение определителя в формуле (5.2) по элементам первой строки:

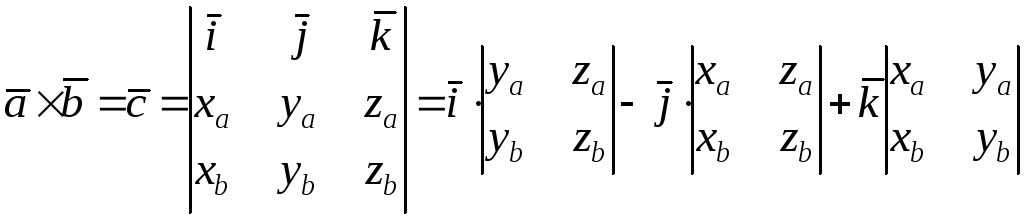
Таким образом, координаты векторного произведения векторов и, т.е. вектораесть:

Т.е.

Из определения векторного произведения следует, что длина вектора равна площади параллелограмма, построенного на векторах

и , значит,

(5.3)

Равенство (5.3) является геометрическим смыслом векторного произведения.

5.3 Свойства векторного произведения

1.

2.

3.

Векторное произведение коллинеарных векторов равно нулю. Это следует из определения векторного произведения.

5.4 Векторные произведения единичных орт

Рассмотрим векторы . Из определения векторного произведения следует, что:

(5.4)

Очевидны равенства:

(5.5)

Чтобы определить другие векторные произведения векторов , пользуются схемой:

Из схемы видно, что

5.5 Условия коллинеарности и перпендикулярности векторов

Исходя из определения скалярного и векторного произведения векторов, учитывая свойства и приложение этих операций, делаем выводы:

(5.6)

Т.е. скалярное перпендикулярных векторов равно нулю.

Если векторы коллинеарны, то их координаты пропорциональны, т.е. выполняются равенства:

(5.7)

ЛЕКЦИЯ 6

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

6.1 Определение смешанного произведения векторов

Смешанным произведением трёх векторов называется число, равное скалярному произведению векторного произведения первых двух векторов на третий.

(6.1)

Обозначение .

6.2 Смешанное произведение векторов в координатной форме

(6.2)

6.3 Свойства смешанного произведения

1.

2.

6.4 Геометрический смысл смешанного произведения

Смешанное произведение трёх векторов по абсолютной величине равно объему параллелепипеда, построенного на этих векторах.

ЛЕКЦИЯ 7

Элементы аналитической геометрии

7.1 Прямая на плоскости

Уравнение прямой линии, проходящей через точку перпендикулярно вектору:

(7.1)

Уравнение пучка прямых, проходящих через заданную точу :

(7.2)

Уравнение прямой линии, проходящей через

Две заданные точки и:

(7.3)

Уравнение прямой линии с заданным угловым коэффициентом:

(7.4)

Уравнение прямой линии в отрезках на осях:

(7.5)

Общее уравнение прямой линии на плоскости:

(7.6)

В уравнении (7.6) вектором-нормалью прямой является вектор: .

Уравнение прямой, проходящей через точку , параллельно вектору(каноническое уравнение прямой на плоскости):

(7.7)

Параметрические уравнения прямой линии на плоскости:

(7.8)

Расстояние от точки до прямой:

(7.9)