Файловый архив студентов. Файловый архив студентов.
1301 вуз, 5079 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный горный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Вышка

.pdf
Скачиваний:
14
Добавлен:
28.03.2016
Размер:
942.19 Кб
Скачать
☆

96. Пряма

y

5

x

7

для графіка функції

y

6

12

 

 

 

 

 

дотичною. Знайти координати точки дотику (всі випадки).

97. Написати рівняння дотичних і нормалей до кривої

 

 

x

2

 

її перетину з параболою

y

 

.

2

 

 

 

2x

3

3x

2

 

67

x

є

 

 

6

 

 

 

 

 

 

 

 

 

y

 

10

 

у точках

 

2

1

 

 

x

 

 

 

 

 

 

 

 

 

 

 

98. В якій тичці дотична до кривої

y x

5

5x

4

20 x

2

3

 

 

 

буде

перпендикулярна до прямої y 1601 x 7 (всі випадки).

99.Із листа металу 16 10 м2 виготовити відкритого відкритий бак максимального об’єму.

100.Об’єм відкритого циліндричного чана має дорівнювати заданому значенню V . Якими повинні бути радіус основи і висота чана, щоб металу на його виготовлення пішло найменше?

У задачах 101 – 110

графік.

101.

y x 2arctgx

102.

y 16 x(x 1)

3

 

виконати повне дослідження функції та побудувати її

 

 

2x

3

 

106.

y

 

 

 

2

1

 

 

 

x

 

 

 

 

 

 

 

(x 1)

2

107.

y

 

 

x 2

 

 

 

 

 

103.

104.

105.

 

 

 

x

3

 

y

 

 

 

 

3 x

2

 

 

 

y

1

4x2

 

x

 

 

 

 

 

y 2x 2 arcsin x

108.

109.

110.

y

 

x3

 

 

 

 

 

2(x

1)2

 

 

 

x 2

 

2

 

y

 

 

 

 

 

 

 

 

 

x 2

 

 

 

y ln( x

2

2x 2)

 

20

У задачах 111-120 з’ясувати, чи задовольняє задана функція вказаному рівнянню

111.

112.

113.

z( x, y)

x

2

3y

2

;

3y

z

x

z

0;

 

 

 

 

x

y

 

 

 

 

 

 

 

 

 

 

z( x, y) tg

3

(2x 3y);

3

z

2

z

0;

 

 

 

x

y

 

 

 

 

 

 

 

 

 

 

z( x, y) sin

2

(3x 4 y);

4

z

3

z

0;

 

 

 

x

y

 

 

 

 

 

 

114.

z( x, y) ln( x

2

y

2

);

z

 

z

 

2

;

 

 

 

 

 

x

y

x y

 

 

 

 

 

 

 

 

115.

116.

117.

118.

119.

120.

z( x, y)

3

2x

2

y

2

;

 

2 y

 

z

x

z

0;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

y

 

 

 

z( x, y) ln( x

2

xy y

2

);

 

x

z

y

z

2;

 

 

 

 

 

 

 

 

x

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z( x, y) ln(e

x

e

y

);

 

z

 

z

1;

 

 

 

 

 

 

 

 

 

 

 

 

x

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

2

 

 

 

 

 

z

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z(x, y)

 

 

 

 

arcsin xy;

x

2

 

 

xy

 

y

2

0;

3x

 

x

y

 

 

 

 

 

 

 

 

 

 

 

 

 

z( x, y) x

2

y

arc tg xy ;

 

 

x

z

y

z

x

2

y;

 

 

 

 

 

 

 

 

x

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

(2x 3y);

3

 

z

 

2

z

0.

 

 

 

z( x, y) cos

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

У задачах 121 - 130 дослідити функцію на екстремум

121.z(x, y) 16 2x y 3 x2 12 y2 xy y

122.z(x, y) 4(x y) x2 y2

123.z(x, y) x2 y2 y

21

124.

125.

126.

127.

128.

129.

130.

z(x, y) 5 x

2

y

3

xy

 

 

 

z(x, y) x

3

y

3

3xy 1

 

 

z(x, y) 4x

2

3y

2

6xy 4x 6 y 1

 

 

z(x, y) 3x2 2 y2 4xy 2x 4 y 1

z(x, y) 4x

2

2 y

2

2xy 4x 6 y 2

 

 

z(x, y) 2x

2

5y

2

6xy 2x 4 y 1

 

 

 

z(x, y) x

2

2 y

2

 

2xy 4x 2 y 11

 

 

 

У задачах 131 - 140 знайти умовний екстремум функції двох змінних при заданому рівнянню зв’язку.

131.

132.

133.

134.

135.

136.

137.

138.

139.

140.

z(x, y) 4x

2

 

3y

2

6xy 4x 6 y 1,

8x 3y 6.

 

 

z(x, y) 4x

2

 

2 y

2

2xy 4x 6 y 2,

16x 3y 70.

 

 

z(x, y) 3x

2

 

2 y

2

4xy 2x 4 y 3,

7x 2 y 14

 

 

z(x, y) 2x

2

 

3y

2

4xy 4x 2 y 1,

2x 2

 

 

z(x, y) 2x

2

 

3y

2

4xy 4x 6 y 1,

x y 2.

 

 

z(x, y) x2

2 y2

2xy 2x 4 y 10,

x 3y 4

z(x, y) 3x

2

2 y

2

4xy 2x 4 y 1,

 

7x y 9

 

 

 

z(x, y) x

2

2 y

2

2xy 4x 6 y 12,

 

x y 3

 

 

 

z(x, y) x

2

5y

2

4xy 4x 2 y 5,

3x 10 y 11

 

 

z(x, y) x2 2 y2 2xy 4x 2 y 2,

 

3x y 1

У задачах 141 - 150 задано функцію

z(x, y)

a(ax , a y ) . Знайти

а) градієнт функції z(x, y) в точці A(x0 , y0 ) ;

, точку

A(x0 , y0 ) та вектор

22

б) похідну функції z(x, y) в точці A(x

, y ) за напрямом

 

 

 

0

0

141. z( x, y) arc tg x

2

y ;

A(1;1),

a( 4, 3);

 

a(a

x

, a

y

 

 

)

.

142.

z( x, y) ln x sin y ; A(1;0), a(2,1);

143.

z( x, y) arctg

x

; A(1;1), a(1,1);

y

 

 

 

144.

145.

z(x, y) ln

x

2

y

2

;

A(0;1),

a( 5,12);

 

 

 

 

 

 

 

 

 

z( x, y) ln

1 xy

2

 

;

A(1;0),

a(3,4);

 

 

146.

z( x, y) arcsin xy ;

A(1;1),

a( 4,3);

147.

z( x, y) x e

2 y

y e

x

;

A(0;0),

a( 3,4);

 

 

148.

z(x, y)

 

xy

 

2 ;

A(1;1),

a(12, 5);

1

 

149.

150.

z( x, y) z( x, y)

sin x arctg

e

x2

2 y

;

 

y ;

A(1;0),

a(5, 12);

A(1;1),

a(1,1).

У задачах 151-160 знайти невизначені інтеграли.

 

151. а)

x

5x2 2dx ;

 

 

 

б)

 

x2e3xdx ;

 

 

x

2

1

 

 

 

 

 

x

 

 

 

 

 

 

 

 

г)

 

 

dx ;

д)

 

 

 

dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x(x 1)(x 1)

 

3x

3

x

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

152.

а)

 

 

dx

;

 

 

б)

 

ln( x

2

1)dx

;

 

(3x 2)7

 

 

 

 

 

x

2

x

4

 

 

 

 

1 x

 

dx

 

 

 

 

г)

 

dx ;

д)

 

 

 

.

 

 

 

 

 

 

 

 

 

 

1 x

 

 

 

 

 

(x 3)(x 1)(x 2)

 

 

 

 

x

 

 

 

 

23

в)

в)

 

3x 6

dx

2

 

x

4x

5

 

dx

2 3x 2x2

;

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1/ x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

153.

 

 

 

а)

 

 

 

 

 

e

 

 

 

 

 

 

 

dx ;

 

 

 

 

 

 

 

 

 

б)

 

 

 

arctg

xdx ;

 

 

 

 

 

 

 

 

 

 

 

 

 

x

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5x

3

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cos

2

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

 

 

 

 

 

 

 

dx ;

 

 

 

 

 

 

 

 

д)

 

 

 

dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

3

5x

2

4x

 

 

 

 

 

 

 

 

 

sin

6

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

154.

 

 

 

а)

 

 

ex sin( ex )dx ;

 

 

 

 

 

 

 

 

б)

 

 

 

ln x

dx ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

2x

2

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

 

 

 

 

 

 

 

 

dx ;

 

 

 

 

 

 

 

 

д)

 

 

sin x cos

xdx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

3

5x

2

6x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

155.

 

 

 

а)

 

 

ecos x sin xdx ;

 

 

 

 

 

 

 

б)

 

 

 

xarctgx

 

dx ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 x2

 

 

 

 

3x

2

 

2x 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 x

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

 

 

 

 

dx

;

 

 

 

 

 

 

 

 

д)

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(x 1)

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

x

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(x 2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

156.

 

 

 

а)

 

 

 

cos(ln x)

dx ;

 

 

 

 

 

 

 

б)

 

 

e

x / 3

x

3

dx ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5x

2

 

6x 9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cos xdx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

 

 

 

 

 

 

 

dx

;

 

 

 

 

 

 

 

 

д)

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

(x

3)

2

(x

1)

2

 

 

 

 

 

 

 

 

 

(1 cos x)

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

157.

 

 

 

а)

 

 

 

cos

 

 

 

 

 

x

dx ;

 

 

 

 

 

 

 

 

б)

 

 

x2 ln(1 x)dx ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

д)

 

 

 

dx

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(x2 1)( x2 x)

 

 

 

 

 

 

1 tgx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

158.

 

 

 

а)

 

 

 

 

 

dx

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

б)

 

 

 

arcsin

x dx ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x ln

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

 

 

(2x2 3x 3)dx

;

 

 

 

 

 

 

 

 

д)

 

 

 

 

 

dx

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(x 1)( x

2

2x 5)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3cos x 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

159. а)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

б)

 

 

ln(ln x)

dx ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

3x

 

 

1 9x

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

arccos

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

 

 

 

 

 

 

 

2xdx

 

 

 

 

 

;

 

 

 

 

д)

 

 

3sin x 2 cos x

dx .

 

 

 

 

 

 

 

 

 

 

 

(x

1)( x2

 

1)3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2sin x 3cos x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

24

 

 

 

 

 

 

 

 

 

 

 

 

 

в)

в)

в)

в)

в)

в)

в)

 

(4x 3)dx

x

2

2x 6

 

 

 

 

(x 4)dx

 

2 x

2x

2

 

 

 

 

(3x 2)dx

x

2

4x 5

 

 

 

 

(8x 11)dx

5 2x x

2

 

 

 

 

(x 3)dx

 

3 2x x

2

 

 

 

xdx

x2 x 1

(2x 5)dx

9x2 6x 2

;

;

;

;

;

;

;

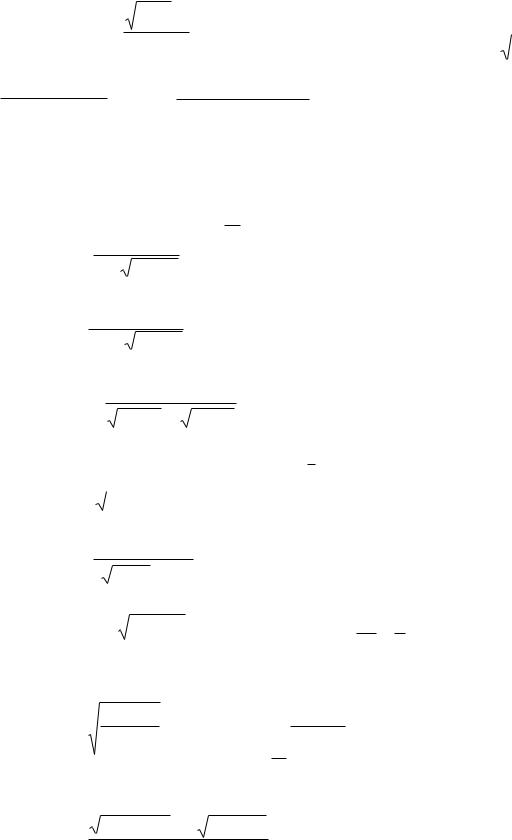
г)

 

 

 

 

 

 

tg

3

xdx

 

 

 

x3x dx ;

 

 

(2 5x)dx

 

 

160. а)

 

 

 

 

;

 

б)

в)

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

cos

x

 

4x2 9x 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(x 2)dx

 

;

д)

 

 

 

 

 

cos x

dx .

 

 

 

 

 

 

2

2x 2)

3

 

 

 

2

x 6sin x

 

 

 

 

 

 

(x

 

 

 

 

 

 

sin

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У задачах 161 – 170 обчислити визначені інтеграли.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

20

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

12

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

161. а)

 

 

 

 

 

 

 

 

 

;

 

б)

 

 

2

cos3xdx .

 

 

 

 

 

 

 

 

 

 

5

3x

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

162. а)

 

 

 

 

 

 

 

 

 

 

;

 

б) x log22 xdx .

 

 

 

 

 

 

 

 

 

 

21

 

7x 5

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

32,5

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

2

 

 

 

 

 

 

 

 

 

 

163. а)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

; б)

(x

x

20) sin 2xxdx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2x

1

3

 

2x 1

 

 

 

1

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

63

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

164. а)

 

 

 

 

 

 

 

;

 

 

б)

(x

 

 

1)

3

 

 

dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

26

x 1

2

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

25

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

2

 

 

 

x

 

 

 

 

 

 

 

 

165. а)

 

 

 

 

 

 

 

 

 

 

 

;

 

б)

 

(2x x

 

) 5

dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

x 2

 

3)

2

 

 

 

 

 

 

 

 

 

 

 

 

1

(

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2,5

2

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

x

3

 

3

 

2

 

166. а)

 

 

x

25 x

dx ;

 

б)

 

(x

3x) ln(

 

 

x

)dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

2

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

2tgx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

x

 

1

 

 

 

 

 

 

 

 

 

167. а)

5

 

 

cos 2xdx ;

 

 

б)

 

 

 

 

 

dx .

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

1 tg

x

 

 

 

 

 

 

 

 

 

 

 

 

 

sin

2x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

1

cos 2x

3

ctgx 2

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

168. а)

 

 

dx

; б) (2x2 7x) sin 4xdx .

 

 

 

 

 

 

 

 

sin

2

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

25

169.а)

170.а)

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2

 

 

 

 

 

x cos

x

 

sin

 

 

 

 

 

12

 

 

 

 

 

 

 

 

 

 

 

 

7 3

 

5

(x

1)

 

 

 

 

 

log

2

dx

;

 

 

 

 

 

 

 

 

 

x 1

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2tgx

 

1 tg

2

x

 

 

 

 

 

 

 

4

 

 

x

б)

 

4

 

 

 

 

0

 

 

 

 

1

 

 

 

 

2

dx

 

cos

 

 

 

2x

sin 2xdx .

;

 

 

 

3

x 5

 

б)

dx .

 

 

cos2 x

3

 

 

У задачах 171 – 180 виконати вказані завдання.

 

171.

Обчислити площу

фігури,

обмеженої

лініями y 2x2 5x 1 та

y 2x 2 .

 

 

 

 

 

 

 

172.

Обчислити об’єм тіла, одержаного обертанням навколо

осі абсцис

фігури обмеженої лініями y

4x x

2

та

y 2x .

 

 

 

 

 

173.

Обчислити

площу

фігури,

обмеженої

лініями

y log

2

x,

y 2

x

 

 

 

 

 

174. Знайти фігури, обмеженої

,

x 2,

x 4 .

 

 

об’єм тіла, утвореного

лініями y 6x x2 та

y

обертанням навколо осі ординат

0 .

175. Знайти площу фігури, обмеженої лініями

 

x

2

y

 

2

 

та

y

1

 

1 x

2

 

 

 

.

176.

Знайти координати центра

ваги однорідної плоскої

(густина

поверхневої

речовини

const ),

обмеженої

пластини

лініями

y sin x,

y 0,

x

 

.

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

177.

Знайти

 

об’єм тіла, утвореного обертанням навколо осі ординат

фігури, обмеженої лініями ч та

y x

2

3

.

 

 

 

 

178.

Знайти

площу фігури,

обмеженої трипелюстковою трояндою

a sin3 .

 

 

 

 

 

 

 

 

26

179. Знайти координати центра

(густина поверхневої речовини

ваги однорідної плоскої

const ),

обмеженої

пластини

лініями

y ln x,

y 0,

 

 

x e

2

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

180.

Знайти

об’єм тіла, утвореного

 

обертанням навколо

осі

абсцис

частини фігури,

 

обмеженої

лініями

y x

3

та

y 2x x

2

(взяти

ту

частину

 

 

 

фігури, що знаходиться в першій чверті системи координат).

 

 

 

В задачах 181 – 190 обчислити довжину дуги кривої.

 

 

 

 

181.

y

2

x

3

,

x

2

y

2

12 (йдеться про частину напівкубічної параболи,

 

 

 

 

 

що знаходиться всередині кола).

 

 

 

 

 

 

 

 

182.

y x

3

,

 

x y 2

(йдеться

про

частину параболи між

точками її

 

 

 

перетину з прямою).

183.

184.

185.

x 5(t

sin t)

,

 

 

 

 

 

y 5(1

cost)

2(1 cos ),

 

 

3

t

 

 

x a cos

 

,

0

 

 

 

 

y a sin3 t

 

 

 

 

 

 

 

 

 

t

2

 

t 2

.

.

.

186.

x

 

знаходиться

2

y

3

,

y

 

 

всередині

x

2

(йдеться про частину напівкубічної параболи, що

 

 

 

«звичайної» параболи).

187.

y ln( 2sin

x

cos

x

),

2

2

 

 

 

6

x

 

3

 

.

 

 

t

cos 2t

 

 

 

 

 

 

 

 

 

 

 

188.

x e

 

,

ln

t ln

.

 

 

 

 

 

 

 

 

y et sin 2t

 

 

 

 

4

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

189.

y ln

 

 

 

1 cos2x

,

 

 

 

x

.

 

 

 

 

 

 

 

 

2

 

 

 

 

12

 

 

8

190.

y 4x x2 ,

 

y 2x

(йдеться про частину параболи між точками її

перетину з прямою).

27

У задачах 191 – 200 обчислити невластиві інтеграли або довести їх

розбіжність.

 

 

 

 

 

 

 

191. а)

(x 1)arctx(x 1)dx

 

0

 

 

 

 

 

 

 

 

 

 

 

 

192. а)

 

x ln(x 1)dx

 

 

1

 

 

 

 

 

 

 

 

dx

 

 

193. а)

 

 

 

 

x

x 1

 

 

1

 

 

 

 

 

 

 

 

 

x

2

 

 

194. а)

 

x5

dx

 

 

 

 

 

 

 

0

 

 

 

 

 

 

sin

1

 

 

x

 

195. а)

 

 

 

dx

x

2

 

2 /

 

 

 

 

 

 

 

 

 

 

x

196.а) 1 (x 1)3dx

б)

б)

б)

б)

б)

б)

1

1/ x2

 

 

 

 

 

 

e

 

 

 

 

 

dx

 

 

 

 

x3

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

x

2

4x 3

0

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

3

 

(2 x)

2

 

 

0

 

 

 

 

 

 

 

 

1

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

.x

2

(1

x

2

)

0

 

 

 

 

 

 

 

 

 

 

 

 

 

e

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

.x ln x

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

(1 x)

4

 

 

0 .

 

 

 

 

 

 

 

arctg2x

 

197. а)

 

dx

 

 

x

2

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

198. а)

 

1 cos x

 

dx

 

 

 

 

 

 

 

 

1

3 x2 5

 

 

 

 

 

 

dx

 

198. а)

 

 

 

 

 

 

 

 

 

 

 

 

 

x2

2x 2

 

1

 

 

 

 

 

 

 

 

 

 

 

cos

1

 

 

 

 

x

 

 

199. а)

 

 

 

 

dx

 

 

x3

 

 

2 /

 

 

 

 

 

 

 

 

 

 

 

 

5 arctg2x

200.а) 0 1 4x2 dx

б)

б)

б)

б)

б)

2

 

 

 

 

 

 

 

 

 

 

 

 

ln(x 1)dx

1

 

 

 

 

 

 

 

 

 

 

 

 

1

x

1

 

 

 

 

 

 

 

dx

3

x

7

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

1

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

x x

2

 

0

 

 

 

 

 

 

 

 

 

 

1

 

e

2 / x

dx

 

 

 

 

 

 

 

 

 

x2

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 1

x2

0

 

28

Узадачах 201 –211 виконати вказані завдання.

201.Знайти роботу потрібну на будування правильної трикутної піраміди

з висотою Н та стороною основи а. Гущина матеріалу .

 

 

202. Знайти роботу потрібну на викачування рідини гущиною

 

з котла в

формі конуса розташованого вершиною вниз. Радіус основи конуса R,

висота Н.

203. Знайти роботу потрібну на розтягування мідної проволоки

довжиною L з площею поперечного

перетину S

на величину

Н = 0,001S. Сила натягнення визначається законом Гука: F ESx / L .

204. Знайти силу тиску рідини з гущиною

на вертикальне розташовану

в неї пластину, якщо пластина має форму трапеції висотою

Н, з нижній

основою а та верхньою основою b. Верхня основа пластини співпадає з рівнем рідини.

205. Знайти роботу потрібну для викачування рідини з гущиною з сосуду в формі горизонтального циліндру довжиною Н та радіусом основи R.

206. Знайти роботу потрібну на будування споруди у формі полу кулі радіусу R розташованого вершиною вверх. Гущина матеріалу .

207. Знайти силу тиску рідини з гущиною на вертикальне розташовану в неї пластину, якщо пластина має форму кола радіуса R та торкається поверхні рідини.

208. Знайти роботу потрібну на виїмку ґрунту з котловану у формі усіченого конусу з висотою Н та радіусами основ R1 та R2. Гущина ґрунту.

209. Знайти силу тиску рідини з гущиною на вертикальне розташовану в неї пластину, якщо пластина має форму рівнобічного трикутника з висотою Н, основа якого розташована паралельно рівню рідини і знаходиться на глибини 2Н а протилежна до основи вершина знаходиться на глибини 3Н.

29

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности