В.В.Поступаев * Физика плазмы, тема 16
Ускоряющаяся Вселеннаяя
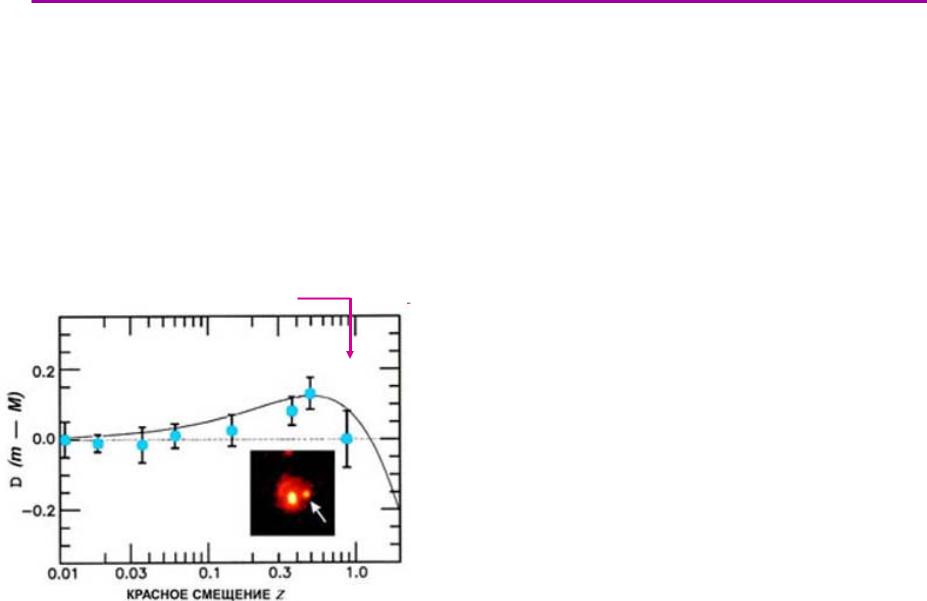
Мы видим удалённые галактики в далёком прошлом. Поэтому можно узнать скорость расширения Вселенной в ранние эпохи. В стандартной физике скорость расширения должна замедляться из-за
противодействия гравитационного поля.
Нобелевская премия по физике 2011 года: Saul Perlmutter, Brian P. Schmidt и Adam G. Riess
«за открытие ускоренного расширения Вселенной по наблюдениям далёких сверхновых звёзд»
6 млрд. лет
По горизонтали: красное смещение z
По вертикали – разность между теоретической яркостью m и реально наблюдаемой M.
До момента 6 млрд. лет назад Вселенная замедляла расширение, как ей и положено по обычной физике. Но после этого она стала ускоряться!
→есть новая сущность – тёмная энергия, которая отвечает за это расширение
http://www.modcos.com/images/articles/den/2011/11/007.jpg
В.В.Поступаев * Физика плазмы, тема 16
Гравитационная неустойчивостьость
Приводит к возникновению видимой структуры мира Рассматривается однородная среда с учетом поля тяжести и давления вещества.
Было: В МГД-модели плазма рассматривается как сплошная среда.
• |
|
Уравнение движения: ρ u = − P + ρg |
(1) |
u (r ,t ) - скорость среды, P (r ,t ) - давление, ρ(r ,t)= mn - плотность
g – аналог вектора E в электродинамике
Электромагнитное |
E = e/r2 |
f = e/r |
E = -gradϕ |
ϕ = −4πρ |
поле |
|
|
|
|
Гравитационное |
g = -Gm/r2 |
f = -Gm/r |
g = -gradϕ |
ϕ = 4πGρ |
поле |
|
|
|
|
В.В.Поступаев * Физика плазмы, тема 16
Замыкаемсистему уравненийний
ϕ = 4πGρ
∂∂ρt +div ρu = 0
Уравнение Пуассона |
(2) |
Уравнение непрерывности |
(3) |
P ~ ργ |
Уравнение адиабаты |
(4) |
Устойчивость структуры исследуется методом малых возмущений
Исходное состояние - |
Вводим малое возмущение: |
неподвижное, однородное вещество: |
|
u = 0 |
u = δu |
g = 0 |
g = δg |
ρ = ρ0 |
ρ = ρ0 + δρ |
P = P0 |
P = P0 + δP |
В.В.Поступаев * Физика плазмы, тема 16
Решениесистемы уравненийний
•
ρ0 δu = − δP + ρ0δg
|
−divδ g = 4πGδρ |
Пусть |
f = divδu |
|
|
|
|
∂δρ |
+ ρ0 divδu = 0 |
c 2 |
= dP/dρ = γP |
/ρ |
|
– скорость звука |
|
∂t |
0 |
|
|
s |
|
0 |
|
|
δP/P0= γδρ/ρ
Получим решение системы в виде:
|
∂2 f |
= cs2 |
f + 4πGρ0 f |
|
∂t2 |
волновое уравнение |
|
|
|
|
|
Раскладываем возмущение на гармонические функции: f = F(t)·exp(-ikr)
F″+(k2cs2-ω02)F = 0, где ω02 = 4πGρ0
Анализрешения В.В.Поступаев * Физика плазмы, тема 16
F exp(νt), где
ν = 
ω02 −k 2cs2
Для малых k < kкр возмущения экспоненциально нарастают → неустойчивость
Для больших k > kкр получаем колебательные решения → устойчивость
На больших расстояниях преобладает Fтяг На малых – давление препятствует сжатию
При k=kкр – граница неустойчивости, длина соответствующая kкр:
λДж = сs π |
Gρ0 |
- Джинсовская длина волны * |
|
|
|
|
|
Теория Джинса формально ошибочна, т.к. g ≠ 0 при ρ0 = const → Однородное распределение плотности нестационарно, т.е. ρ0 = ρ0(t). Однако, эта теория помогает правильно понять суть процесса.
* J.H. Jeans. The Stability of a Spherical Nebula // Philos. Trans. of the Royal Soc. of London. Ser. A, Vol. 199, pp. 1-53 (1902)
В.В.Поступаев * Физика плазмы, тема 16
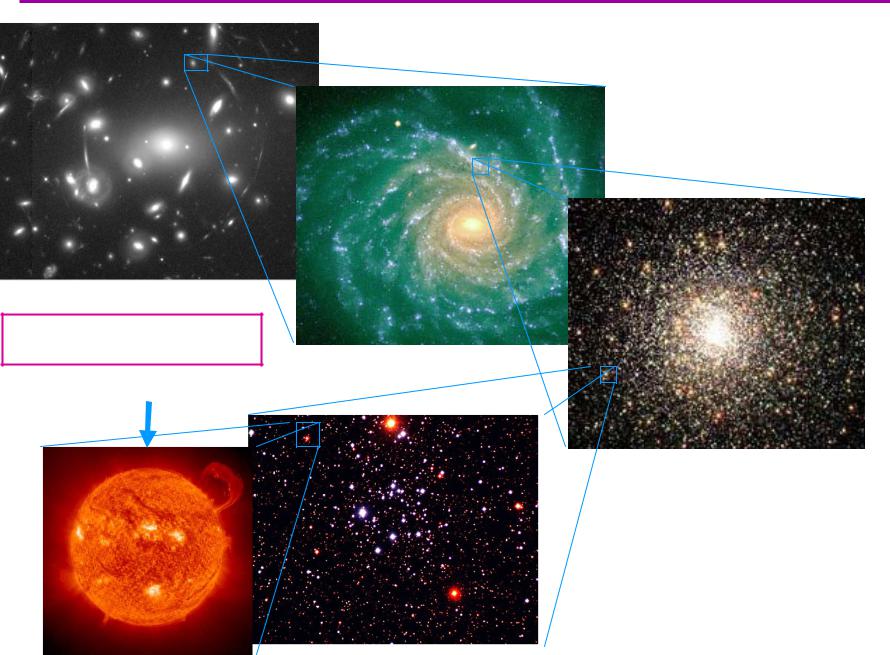
Фрагментациявеществаво Вселеннойленной
Скопления галактик ~1012 M
Галактики ~109 M
MДж= ρ0(λДж /2)3
– масса Джинса
В процессе остывания вещества во Вселенной образовывались структуры разного масштаба
Шаровые скопления ~106 M
Ход фрагментации зависит от начального спектра возмущений
Группы звезд ~102 - 103 M
Звезды M > MДж
