В.В.Поступаев * Физика плазмы, тема 13
Многопробочная ловушкака
Принцип действия |
|
Г.И.Будкер, В.В.Мирнов, Д.Д.Рютов, 1971 |
|
|
|
|
|
|
|
пролётные частицы |
|
запертые частицы |
|
|
|
|
|
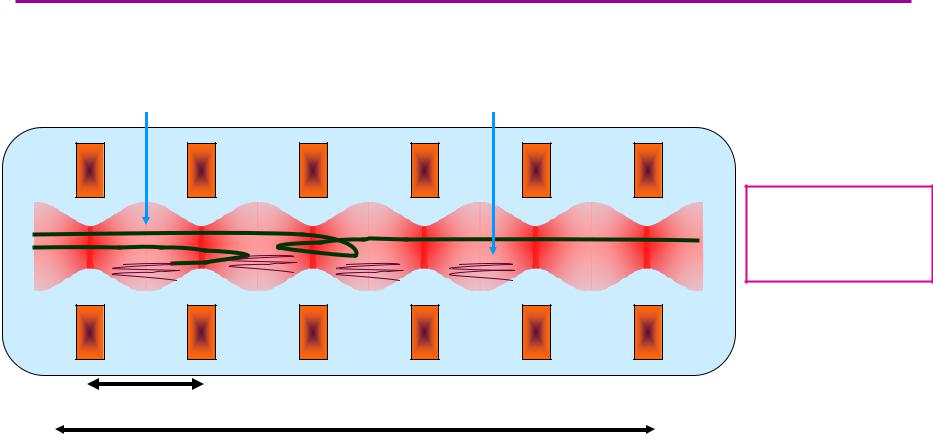
Условие:
l < λ << L
l - период гофрировки |
L - продольный размер |
Без гофрировки скорость расширения плазмы - V В гофрированном поле появляется сила трения между пролетными и запертыми частицами.
Свободный разлет плазмы сменяется диффузией:
В.В.Поступаев * Физика плазмы, тема 13
Удержаниевмногопробочной ловушкеловушке
Рассмотрим многопробочную ловушку с периодом гофрировки l порядка длины свободного пробега заряженных частиц λ. При этом выполняется условие l << L (L - длина ловушки). Тогда ловушку можно рассматривать как последовательность пробкотронов (ячеек), в которых плазма состоит из захваченных и пролетных частиц. При l << λ запертые частицы совершают множество колебаний в каждом пробкотроне (ячейке) между столкновениями, так что перенос вещества и энергии происходит только за счет пролетных частиц, которые испытывают трение о захваченные частицы, передающие, в свою очередь, импульс магнитному полю. Организованное таким путем «трение» плазмы о магнитное поле можно оценить следующим образом. Сила трения, отнесенная к одному иону, имеет величину:
Fтр ~ mi ·νii ·u,
где νii – частота ионных столкновений, а u – скорость направленного движения пролетных ионов, близкая к макроскопической скорости движения плазмы при умеренных значениях пробочного отношения k - 1 = Hmax/Hmin - 1 ~ 1. Из условия равенства силы трения n·Fтр и градиента давления плазмы:
∂nT / ∂z ~ nT / L
определяется скорость расширения плазмы: |
u ~ υTiλ / L <<υTi |
В.В.Поступаев * Физика плазмы, тема 13
Времяжизнивмногопробочной ловушкеловушке
L l
Пусть длина соленоида L превышает длину свободного пробега λi. Если, в то же время, длина ячейки l ~ λi , то время продольного удержания существенно увеличивается по сравнению с классической пробочной ловушкой.
τ R2 |
L2 |
= R2 |
L |
τ0 |
R = |
Bmax |
|
|
|
|
λi VTi |
λi |
Bmin |
τ0 ~ |
L |
- время удержания в простом соленоиде |
|
|
VTi |
|
|
|
|
|
|
В.В.Поступаев * Физика плазмы, тема 13
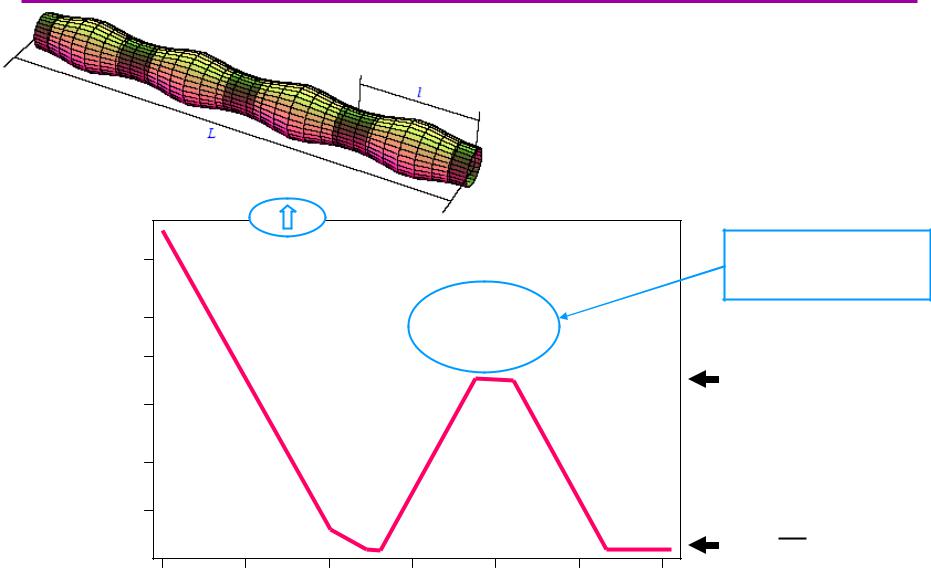
Областьпараметров плазмымы
|
|
|
|
|
|
Расчет энергетического времени жизни |
|
|
|
|
|
|
плазмы по «классическим» формулам |
|
|
|
|
|
|
|
|
|
R=1.5 |
|
|
|
|
|
|
|
|
|
l = 22 см |
|
токамаки |
|
|
|
|
|
L/l = 55 |
|
|
|
|
|
|
|
|
5000 |
λi >> l >>L |
|
|
Ti=1кэВ |
многопробочное |
|
|
|
|
|
удержание |
|
|
|
|
|
|
|
|
|
, мкс |
2000 |
|
|
|
|
λi ~ l |
|
|
|
жизни |
1000 |
|
|
|
|
|
|
|
τ ~τ0 L / l |
|
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
Время |
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
τ0~ VL |
|
|
|
|
|
|
|
|
|
|
|
1012 |
1013 |
1014 |
1015 |
1016 |
1017 |
1018 |
T |
|
|
|
|
|
|
|
Плотность, см-3 |
|
|
|
В.В.Поступаев * Физика плазмы, тема 13
Многопробочная ловушка ГОЛОЛ--33
В.В.Поступаев * Физика плазмы, тема 13
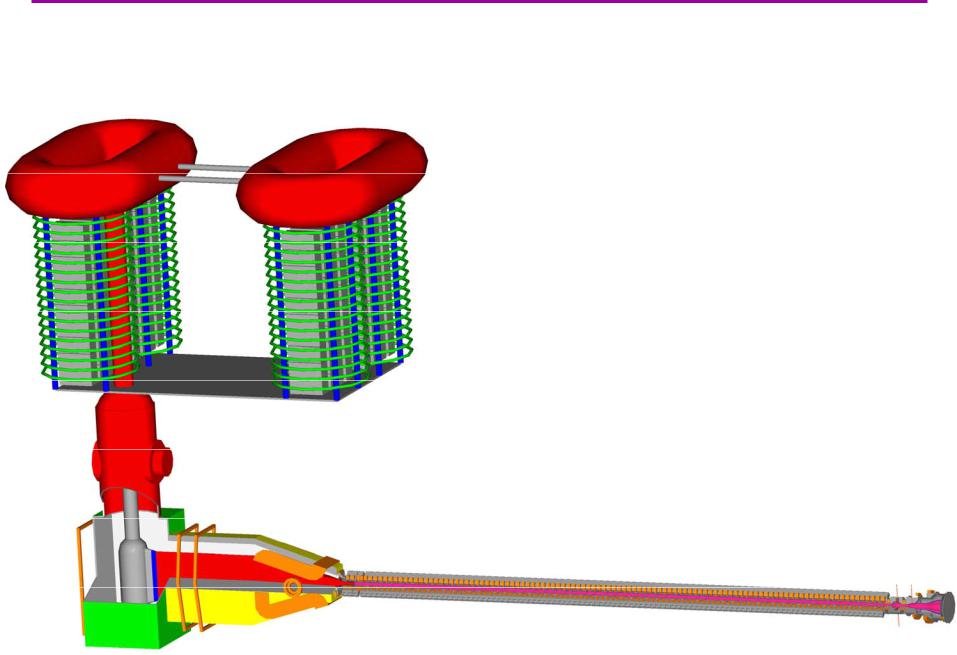
Схемамногопробочной ловушкики ГОЛГОЛ--33
Для быстрого нагрева плазмы в ловушке используется релятивистский электронный пучок
Генератор
электронного пучка У-2
Ленточный диод
Плазма
•длина 12 м
•1014- 1016 см-3
•температура ~1 кэВ
Электронный пучок
•1 МэВ
•50 кА
•8 мкс
•до 300 кДж
Магнитное поле
•многопробочное
•55 ячеек
•4.8/3.2 Tл
Гофрированное магнитное поле
В.В.Поступаев * Физика плазмы, тема 13
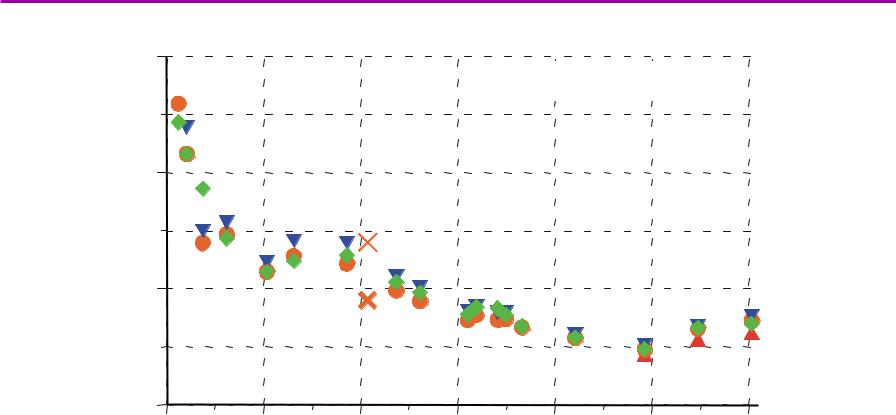
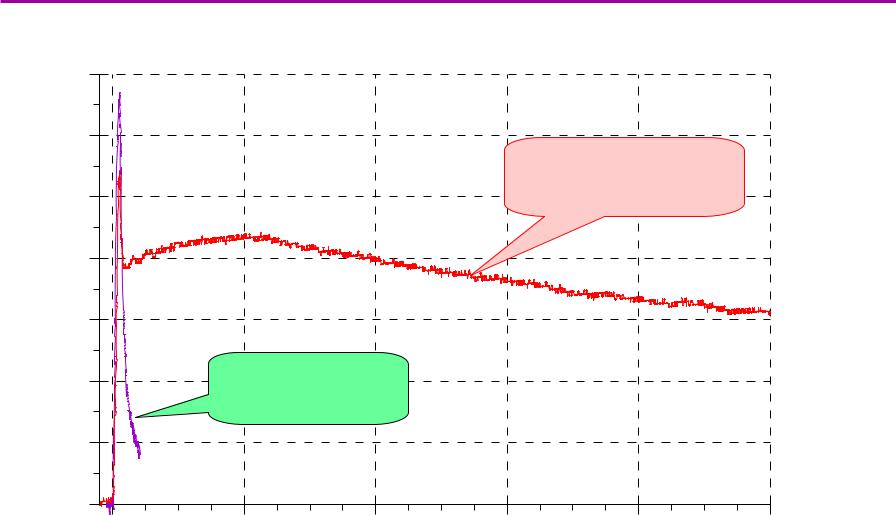
Нагревплазмыэлектронным пучкомпучком
Электронная температура, кэВ
данные диамагнитных измерений и томсоновского рассеяния ГОЛ-3
3
(0.8÷1)·1015 см-3
2
1
0
Расстояние от входной пробки, м
пучок теряет в плазме до 40% энергии за счёт коллективных эффектов
длина пробега релятивистских электронов в плазме за счёт классических столкновений частиц – несколько тысяч километров
В.В.Поступаев * Физика плазмы, тема 13
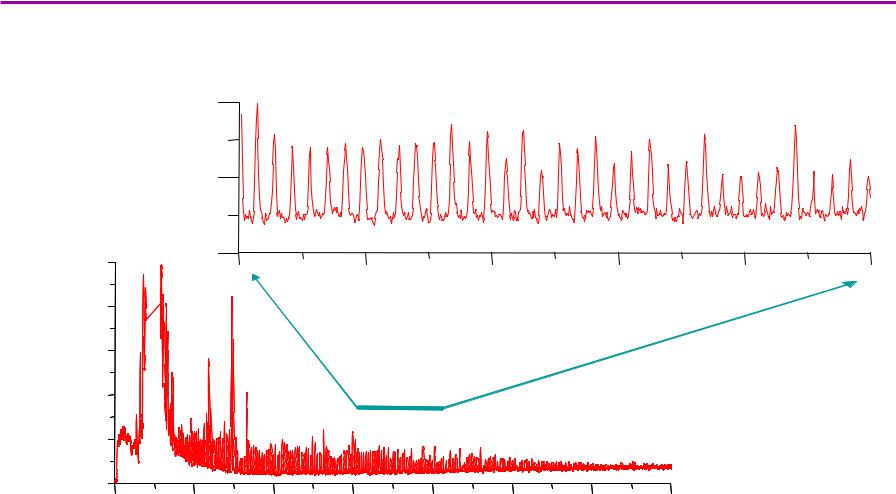
Осцилляциинейтронного потокаотока
ГОЛ-3
intensity of neutron emission, cm-2 c-1
4E+009
2E+009
2E+010 0E+000
2E+010
1E+010
8E+009
4E+009
|
|
|
|
|
|
|
shot #PL6397 |
0E+000 |
|
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
|
|
|
time, microseconds |
|
|
|
В.В.Поступаев * Физика плазмы, тема 13
ГОЛ-3: сравнениес токамакамиками
ГОЛ-3
В.В.Поступаев * Физика плазмы, тема 13
Конецтемы 13
Открытые ловушки. Удержание плазмы в пробкотроне. Принцип среднего min B. Амбиполярная ловушка. Газодинамическая ловушка. Многопробочная ловушка.
В.В.Поступаев * Физика плазмы, тема 14
Новаятема 14
Электрический разрядв газахзах
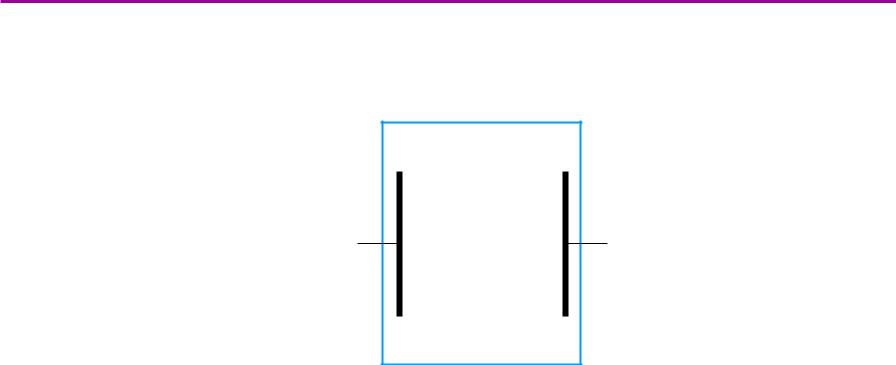
Геометриязадачи В.В.Поступаев * Физика плазмы, тема 14
катод анод
- +
•Слабоионизованная плазма
•Существенная роль нейтральных атомов
•Процессы на поверхности
В.В.Поступаев * Физика плазмы, тема 14
Дрейфэлектроноввплазме - напоминаниеоминание
Ранее получали для полностью ионизованной плазмы: |
|
|
|
|
Формула для электропроводности |
|
|
|
|
|
|
|
|
Используем кинетическое уравнение в тау-приближении |
Stei = |
f0 − f |
|
|
|
|
|
|
|
|
|
τei |
Водородная плазма: e, i |
eE |
|
∂f |
|
|
|
f0 − f |
Кинетическое уравнение для этой задачи имеет вид: |
|
= |
|
me |
|
∂V |
τei |
|
|
|
|
Пусть f = f0 + f1
Пренебрегаем произведением малых сомножителей Тогда:
|
|
|
e2 E |
|
|
ne2 |
|
|
|
|
j = −e |
Vf V |
dV = − |
|
τ |
f |
dV = − |
|
τ |
ei |
E =σ E |
|
m |
m |
|
|
∫ 1 ( ) |
|
|
ei ∫ |
0 |
|
|
|
|
|
|
|
e |
|
|
|
|
e |
|
|
|
В.В.Поступаев * Физика плазмы, тема 14
Дрейфвслабоионизованной плазмеплазме
Для низкотемпературной плазмы основную роль играют столкновения
снейтральными частицами:
τei →τ0
|
ne2 |
|
|
j = −enV = − m |
τ0 E |
Тогда: |
|
|
|
|
|
e |
|
отличие от плазмы: проводимость зависит от концентрации и степени ионизации
Скорость дрейфа электронов в слабоионизованной плазме:
|
V ~ |
eE |
τ |
|
|
|
~ |
|
1 |
|
V |
~ |
eE |
|
1 |
|
|
0 |
τ |
0 |
|
|
|
m n |
σV |
|
m |
n |
σV |
|
d |
|
|
|
|
d |
|
|
|
e |
|
|
|
|
|
0 |
|
|
|
e |
0 |
|
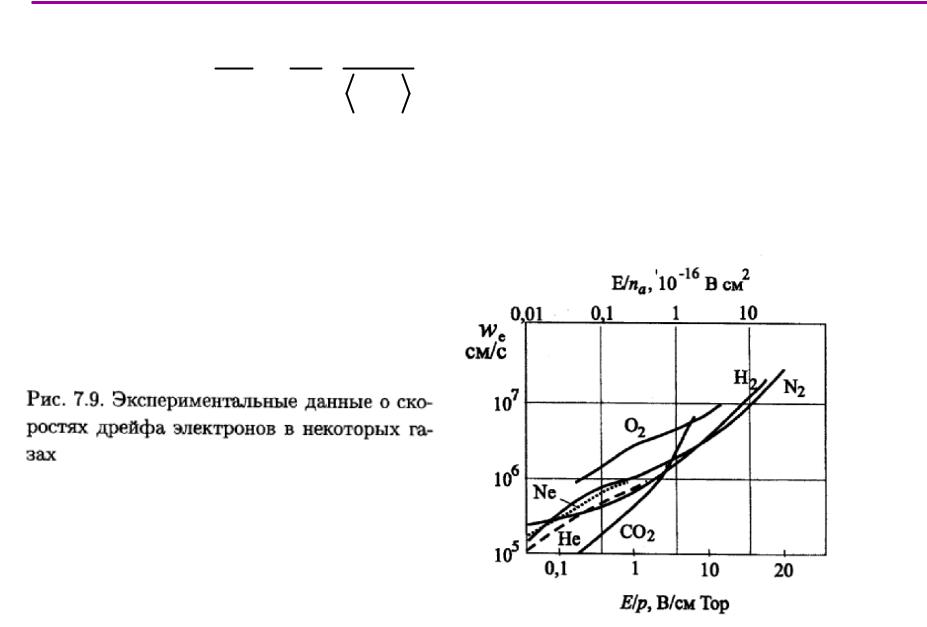
В.В.Поступаев * Физика плазмы, тема 14
Дрейфвслабоионизованной плазмелазме (2)(2)
Vd |
|
e |
|
|
1 |
= μE |
μ - подвижность |
= |
|
E |
|
me n0 |
σV |
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
Параметр |
, или E/p |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Б.А.Князев.“Низкотемпературная плазма и газовый разряд”, Новосибирск, 2003
В.В.Поступаев * Физика плазмы, тема 14
Теорияпробоя Таунсендаа
катод анод
координата z 
Количество свободных носителей малό
(электрическое поле не искажается пространственным зарядом)
Образование лавины и развитие пробоя:
первичные заряженные частицы рождаются случайно эти заряды ускоряются электрическим полем
происходит рождение вторичных частиц и усиление тока (лавина)
есть механизм положительной обратной связи (для стационарности разряда) вторичные частицы рождаются по следующим механизмам:
-ионизация газа электронным ударом (в объёме разрядного промежутка)
-эмиссия с катода из-за бомбардировки ионами (на поверхности электрода)
Б.А.Князев.“Низкотемпературная плазма и газовый разряд”, Новосибирск, 2003
В.В.Поступаев * Физика плазмы, тема 14
Размножениеэлектроновв разрядеазряде
Ионизация эдектронным ударом: |
dn |
|
= n0ne σiV |
|
e |
|
|
dt |
i |
i = ionization |
Если число электронов в газе очень малό, то, до тех пор, пока не “включатся” процессы гибели частиц, число электронов нарастает лавинообразно
ne = ne0 exp(n0 σiV t)
Ионизация при дрейфе электрона в однородном поле.
Поскольку скорость дрейфа электрона Vd = const, то удобно записать скорость рождения заряженных частиц следующим образом:
dn |
|
|
α |
|
E |
|
|
e |
|
=αVd ne , причем |
|
= F |
|
dt |
|
|
n |
|
|
|
i |
n |
|
|
|
|
0 |
|
0 |
|
где α называют первым коэффициентом Таунсенда
Б.А.Князев.“Низкотемпературная плазма и газовый разряд”, Новосибирск, 2003
В.В.Поступаев * Физика плазмы, тема 14
Таунсендовская теория пробояоя (2)(2)
катод
|
|
α |
|
E |
|
|
Таунсенд нашел явный вид |
|
|
|
n |
|
|
= F n |
|
|
|
0 |
|
0 |
|
z 
предположив, что электрон ионизирует атом, если в процессе его ускорения в электрическом поле он достигает энергии, превышающей потенциал ионизации:
e E z > I
Если длина свободного пробега электрона – λ, то вероятность того, что он пройдет без столкновений расстояние z, равна W(z) = exp(-z/λ). На единицу пути среднее число столкновений равно 1/λ, а число пробегов с длиной, большей или равной z, будет P(z) = (1/λ) · exp(-z/λ).
|
|
|
|
|
|
|
|
α - первый коэффициент Таунсенда |
|
I |
|
|
Iλ |
|
|
|
α ≡ P z = |
|
|
= An0 exp |
− |
|
|
|
(количество актов ионизации |
|
|
|
eE |
|
|
eE |
|
на единицу длины пробега) |
|
|
|
|
|
|
|
|
|
Б.А.Князев.“Низкотемпературная плазма и газовый разряд”, Новосибирск, 2003
