
- •Физика плазмы
- •Литература
- •Физика плазмы
- •Вселенная
- •Плазменные технологии
- •Рождение «плазмы»
- •Пространство параметров
- •Пространство параметров (2)
- •Квазинейтральность плазмы
- •Дебаевский радиус
- •Дебаевская экранировка
- •Параметр неидеальности плазмы
- •Формула Сахá
- •Корональное равновесие
- •Резонансная перезарядка
- •Транспортное сечение
- •Проводимость плазмы
- •Низкотемпературная плазма
- •Термоядерная плазма
- •Термоядерная плазма (2)
- •Циклотронное излучение
- •Рекомбинационное излучение
- •Интенсивность линейчатого излучения
- •Доплеровское уширение
- •Функция распределения
- •Кинетическое уравнение
- •Коэффициент теплопроводности
- •Коэффициенты переноса
- •Двухжидкостная магнитная гидродинамика
- •Уравнение теплопереноса
- •Одножидкостная магнитная гидродинамика
- •Одножидкостные МГД-уравнения
- •Уравнение вмороженности
- •Тензор напряжений магнитного поля
- •МГД-неустойчивости Z-пинча
- •Установка MAGPIE – теневые диагностики
- •Желобковая неустойчивость
- •Метод малых колебаний
- •Диэлектрическая проницаемость
- •Электромагнитные волны
- •Распространение радиоволн
- •Интерферометрия плазмы
- •Дисперсионный интерферометр
- •Распространение магнитного звука
- •Циклотронный резонанс
- •Дрейфовое приближение
- •Центробежный дрейф
- •Поляризация плазмы
- •Термоядерные реакции - определение
- •Потенциальная энергия взаимодействия
- •Г. Гамов, Е. Теллер (1938)
- •Радиоактивность термоядерной станции
- •Структура «инерциальной» электростанции
- •NIF – мишень (хольраум)
- •Проект Fusion Test Facility
- •Омический нагрев плазмы
- •Предельный ток разряда
- •Пилообразные колебания
- •Пилообразные колебания - томография
- •Дивертор
- •Бутстрэп-ток
- •Классические стеллараторы
- •Проблемы первых стеллараторов
- •Плазма в LHD
- •Проект W-7X (Германия)
- •Стохастизация магнитного поля
- •Сравнение RFP с токамаками
- •Пробкотрон Будкера-Поста
- •Амбиполярный потенциал
- •Амбиполярная ловушка
- •Параметры GAMMA-10
- •Газодинамическая ловушка
- •Многопробочная ловушка
- •Электронная лавина
- •Плазменная аэродинамика
- •Устройство плазменного дисплея
- •Высокодозная имплантация
- •Плазмохимическое травление
- •Российские плазматроны
- •МГД-генераторы
- •Ускоряющаяся Вселенная
- •Гравитационная неустойчивость
- •Звёзды. Светимость
- •Звёзды. Масса
- •Звёзды. Радиус
- •Гидродинамическое равновесие
- •Крабовидная туманность
- •Электрон-позитронные звёзды
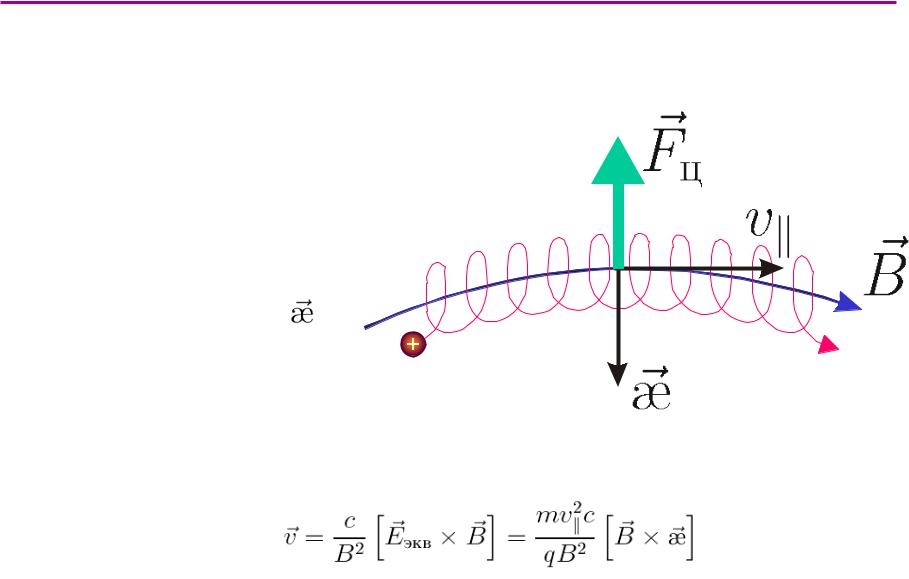
Центробежный дрейфВ.В.Поступаев * Физика плазмы, тема 8
пусть магнитное поле неоднородно в пространстве (есть градиент) рассматриваем продольную компоненту скорости
В системе отсчёта, движущейся вдоль силовой линии со скоростью υװ , на частицу действует центробежная сила
|
mυ2 |
|
F = |
|
; F = mυ2 |
|
||
ц |
|
ц |
|
Rкр |
|
Fц эквивалентна электрическому полю Eэкв = Fц 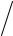 q
q
Дрейф:
Электроны и ионы дрейфуют в разные стороны

В.В.Поступаев * Физика плазмы, тема 8
Магнитныймомент частицыцы
Аналогично выводу дрейфовых уравнений можно преобразовать уравнения
и получить сохранение магнитного момента частицы в магнитном поле:
μ = mυ2 = const
2B
и уравнение, описывающее работу электрического и вихревого магнитного поля:
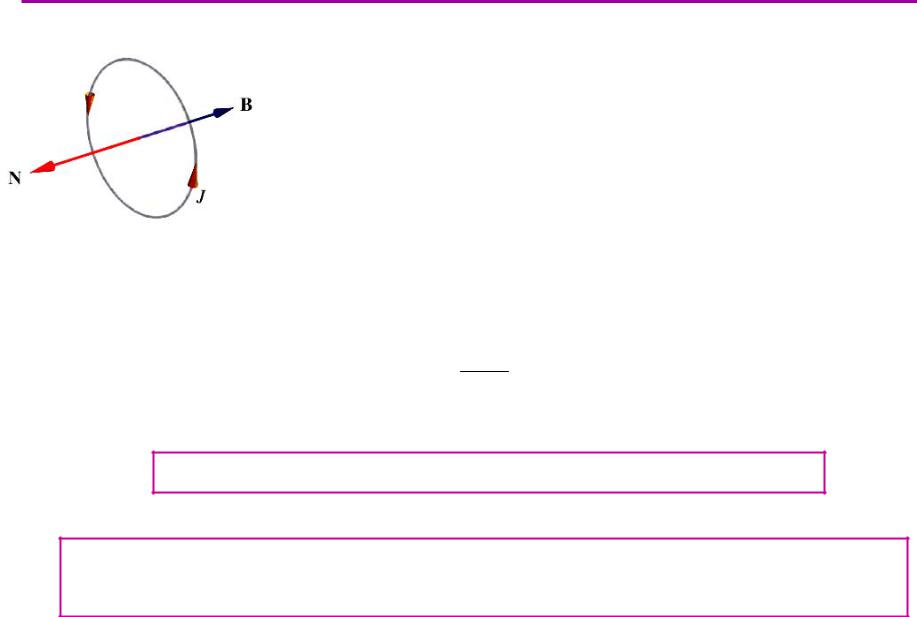
В.В.Поступаев * Физика плазмы, тема 8
Магнитныймомент частицыцы
Движение частицы по окружности в магнитном поле можно представить как элементарный виток с током.
Такой элементарный ток будет производить магнитное поле, эквивалентное полю магнитного диполя.
Поэтому вводим дипольный момент частицы:
μ = |
JS |
N = − |
JS |
|
|
B |
, где |
J = |
qωH |
||
|
|
|
|
|
|
|
2π |
||||
c |
c |
|
|
B |
|
|
|||||
|
|
|
|||||||||
μ = − mυ2 h
2B
поле внутри элементарного контура уменьшается всегда!
В магнитном поле, которое медленно изменяется в пространстве, магнитный момент частицы является адиабатическим инвариантом!
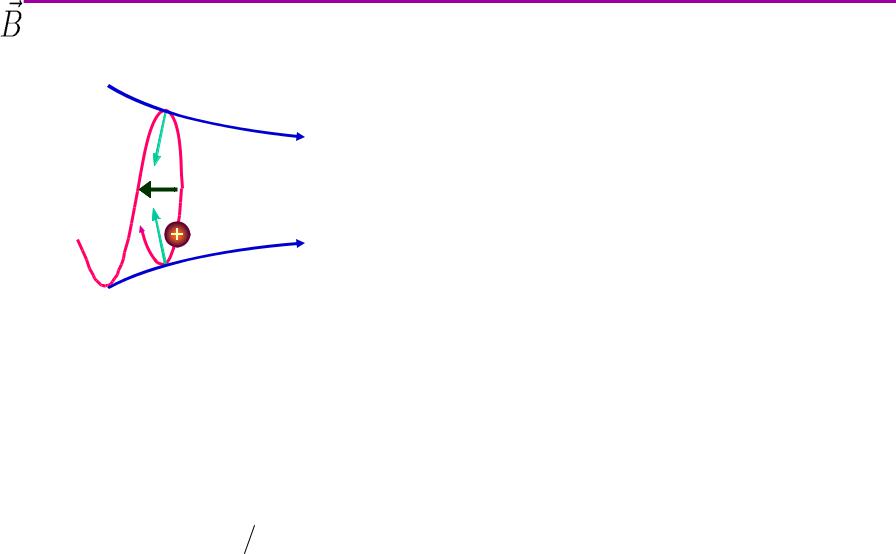
В.В.Поступаев * Физика плазмы, тема 8
Движениевнеоднородном магнитномтном полеполе
|
|
|
|
|
|
|
|
Инварианты движения: |
||||||||||
|
мгновенная сила |
|
|
энергия частицы |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
средняя |
|
|
|
|
|
|
|
|
ε = |
mυ2 |
|
|
= const |
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
сила |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
частица |
|
|
|
|
|
магнитный момент |
|||||||||||
|
|
|
|
|
|
|
|
mυ2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
μ = |
|
|
= const |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2B |
|
|
|
|
|
|
|
Поскольку |
ε = |
mυ2 |
= |
mυ2 |
+ |
mυ2 |
= |
mυ2 |
+ μB |
и |
υ2 > 0 |
|
|
|||||
|
2 |
|
|
|
|
|||||||||||||
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||||
то в область |
B > ε μ |
частица зайти не может ! |
|
|
|
|
mυ2 |
|
= |
ε − μB ≥ 0 |
||||||||
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В.В.Поступаев * Физика плазмы, тема 8
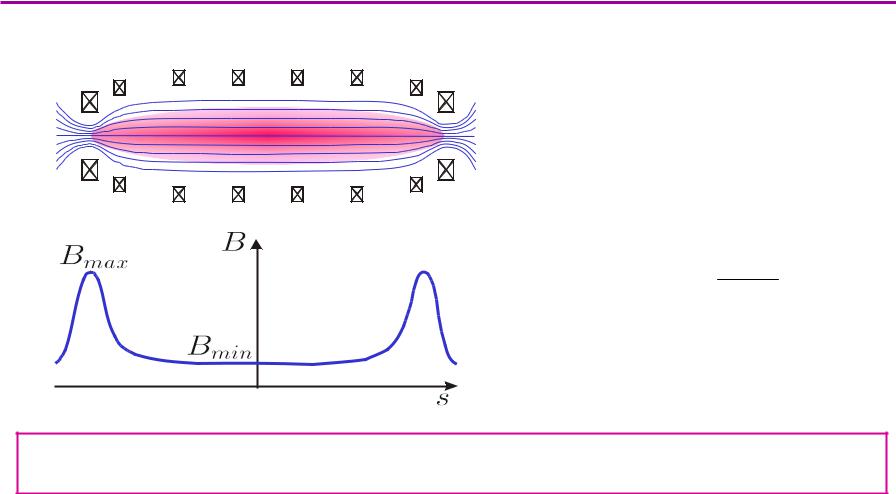
Пробкотрон Будкера-Поста (началоло 19501950хх))
частица удерживается в пробкотроне, если
υ2 (r) > B(r)
υ2 (r) Bmax
частицы с ε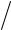 μ > Bmax в пробкотроне Будкера-Поста не удерживаются !
μ > Bmax в пробкотроне Будкера-Поста не удерживаются !
Эксперимент Родионова, 1958 г.: частицы живут более 108 отражений!

В.В.Поступаев * Физика плазмы, тема 8
Удержаниечастицв пробкотронетроне
Если частица стартует из области минимума поля под углом θ :
sinθ |
0 |
= |
υ = |
Bmin |
= R−1/ 2 |
|
B |
||||||
|
|
υ |
|
|||
|
|
|
|
max |
|
пробочное отношение
R ≡ Bmax 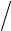 Bmin
Bmin
конус |
удержание |
потерь |
вылет |
Будет ли частица удерживаться, зависит только от угла между вектором скорости и вектором магнитного поля, но не от энергии частицы!
В.В.Поступаев * Физика плазмы, тема 8
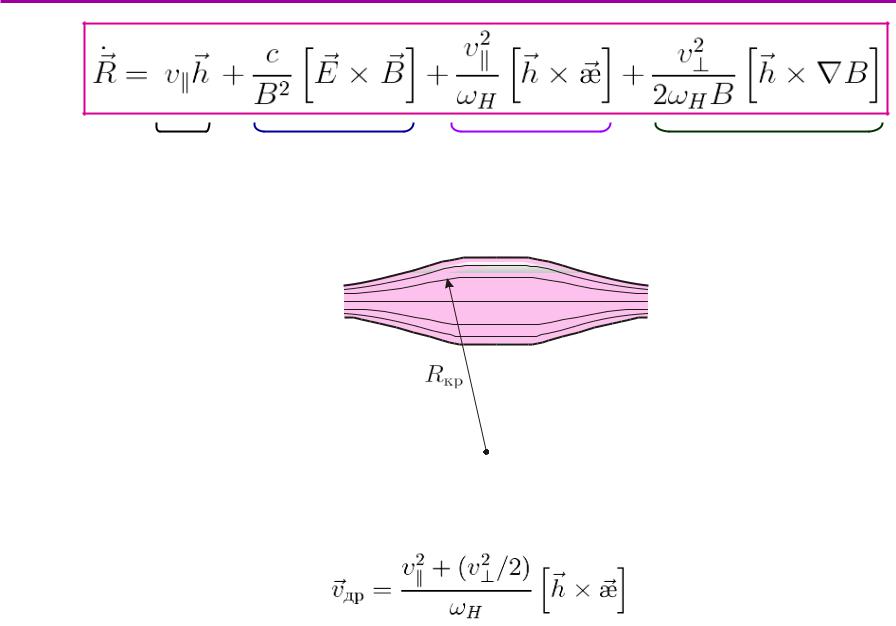
Движениечастицв пробкотронероне
движение вдоль |
электрический |
центробежный |
градиентный |
силовой линии |
дрейф |
дрейф |
дрейф |
пробкотрон
 оба «магнитных» дрейфа (градиентный и центробежный) направлены по бинормали к силовой линии
оба «магнитных» дрейфа (градиентный и центробежный) направлены по бинормали к силовой линии
В.В.Поступаев * Физика плазмы, тема 8
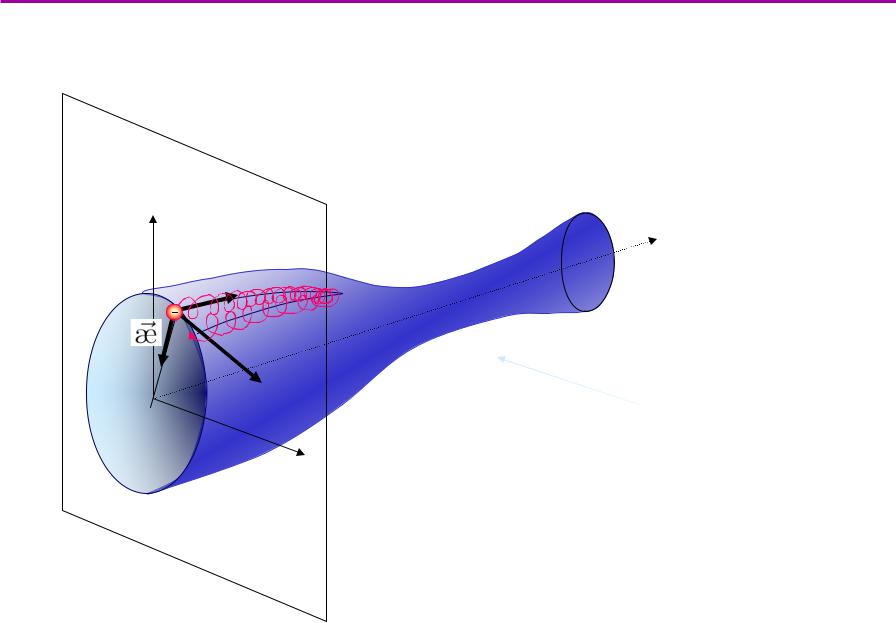
Понятиедрейфовой поверхностиности
Частица быстро осциллирует между пробками и медленно дрейфует в азимутальном направлении
центральная плоскость пробкотрона
(показана одна половинка ловушки)
x
z
h
υдр
y
поверхность – геометрическое множество точек, в которых может оказаться ларморовский центр частицы в ходе её дрейфового движения.
В.В.Поступаев * Физика плазмы, тема 8
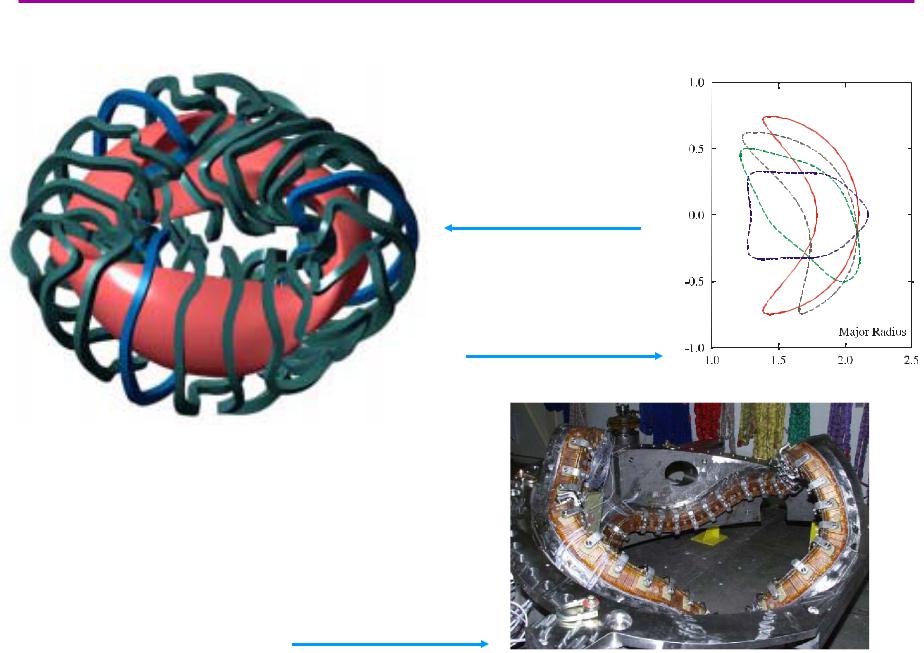
Пример сложнойдрейфовой поверхностиерхности
Проект стелларатора NCSX (Принстон, США)
красным – плазма
синим и зелёным – катушки магнитного поля
разные сечения плазменного шнура
Прототип одной из катушек модульной магнитной системы. Точность магнитного поля – не хуже 10-4 !
В.В.Поступаев * Физика плазмы, тема 8
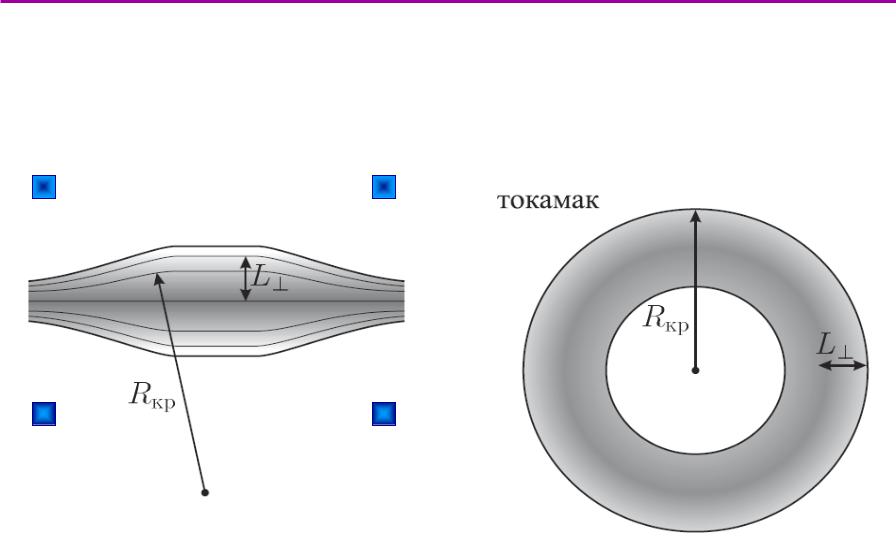
Линейныеитороидальные конфигурацииигурации
пробкотрон Будкера-Поста |
тороидальная система |
||
(отсутствуют потери частиц |
|||
(простейшая открытая ловушка) |
|||
и энергии через торцы) |
|||
|
|||
|
|
|
|
|
|
|
|
В.В.Поступаев * Физика плазмы, тема 8
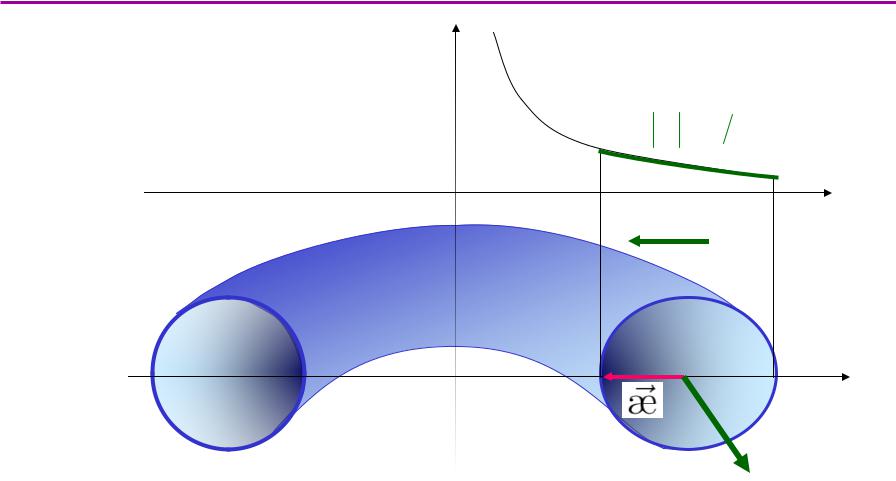
Магнитноеполе тороидаа
B 1 r
B
B
Электроны и ионы дрейфуют в разные стороны
