
- •Физика плазмы
- •Литература
- •Физика плазмы
- •Вселенная
- •Плазменные технологии
- •Рождение «плазмы»
- •Пространство параметров
- •Пространство параметров (2)
- •Квазинейтральность плазмы
- •Дебаевский радиус
- •Дебаевская экранировка
- •Параметр неидеальности плазмы
- •Формула Сахá
- •Корональное равновесие
- •Резонансная перезарядка
- •Транспортное сечение
- •Проводимость плазмы
- •Низкотемпературная плазма
- •Термоядерная плазма
- •Термоядерная плазма (2)
- •Циклотронное излучение
- •Рекомбинационное излучение
- •Интенсивность линейчатого излучения
- •Доплеровское уширение
- •Функция распределения
- •Кинетическое уравнение
- •Коэффициент теплопроводности
- •Коэффициенты переноса
- •Двухжидкостная магнитная гидродинамика
- •Уравнение теплопереноса
- •Одножидкостная магнитная гидродинамика
- •Одножидкостные МГД-уравнения
- •Уравнение вмороженности
- •Тензор напряжений магнитного поля
- •МГД-неустойчивости Z-пинча
- •Установка MAGPIE – теневые диагностики
- •Желобковая неустойчивость
- •Метод малых колебаний
- •Диэлектрическая проницаемость
- •Электромагнитные волны
- •Распространение радиоволн
- •Интерферометрия плазмы
- •Дисперсионный интерферометр
- •Распространение магнитного звука
- •Циклотронный резонанс
- •Дрейфовое приближение
- •Центробежный дрейф
- •Поляризация плазмы
- •Термоядерные реакции - определение
- •Потенциальная энергия взаимодействия
- •Г. Гамов, Е. Теллер (1938)
- •Радиоактивность термоядерной станции
- •Структура «инерциальной» электростанции
- •NIF – мишень (хольраум)
- •Проект Fusion Test Facility
- •Омический нагрев плазмы
- •Предельный ток разряда
- •Пилообразные колебания
- •Пилообразные колебания - томография
- •Дивертор
- •Бутстрэп-ток
- •Классические стеллараторы
- •Проблемы первых стеллараторов
- •Плазма в LHD
- •Проект W-7X (Германия)
- •Стохастизация магнитного поля
- •Сравнение RFP с токамаками
- •Пробкотрон Будкера-Поста
- •Амбиполярный потенциал
- •Амбиполярная ловушка
- •Параметры GAMMA-10
- •Газодинамическая ловушка
- •Многопробочная ловушка
- •Электронная лавина
- •Плазменная аэродинамика
- •Устройство плазменного дисплея
- •Высокодозная имплантация
- •Плазмохимическое травление
- •Российские плазматроны
- •МГД-генераторы
- •Ускоряющаяся Вселенная
- •Гравитационная неустойчивость
- •Звёзды. Светимость
- •Звёзды. Масса
- •Звёзды. Радиус
- •Гидродинамическое равновесие
- •Крабовидная туманность
- •Электрон-позитронные звёзды

В.В.Поступаев * Физика плазмы, тема 8
Циклотронный резонансс
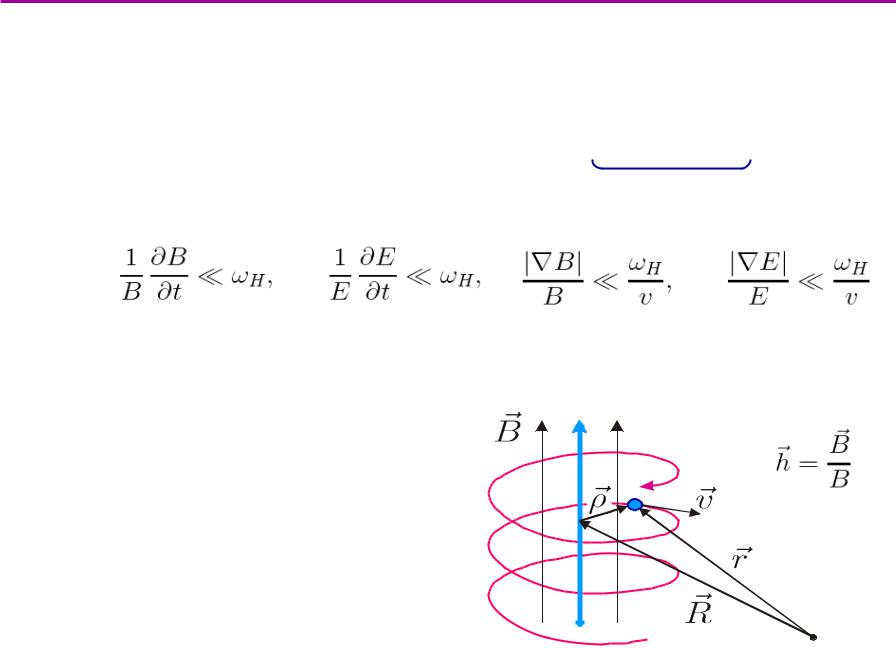
Частица в электрическом и магнитном полях: |
|
dυ |
|
q |
[ |
|
|
|
H ] |
|
||||
|
dt |
= |
m |
E + υ ×ω |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Циклотронный резонанс: |
E |
= |
ω |
|
|
|
ω |
H |
≡ |
qB |
|
|||
|
|
|
|
|||||||||||
|
|
E0 sin( |
H t) |
|
|
|
|
|
|
mc |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 B
B
x
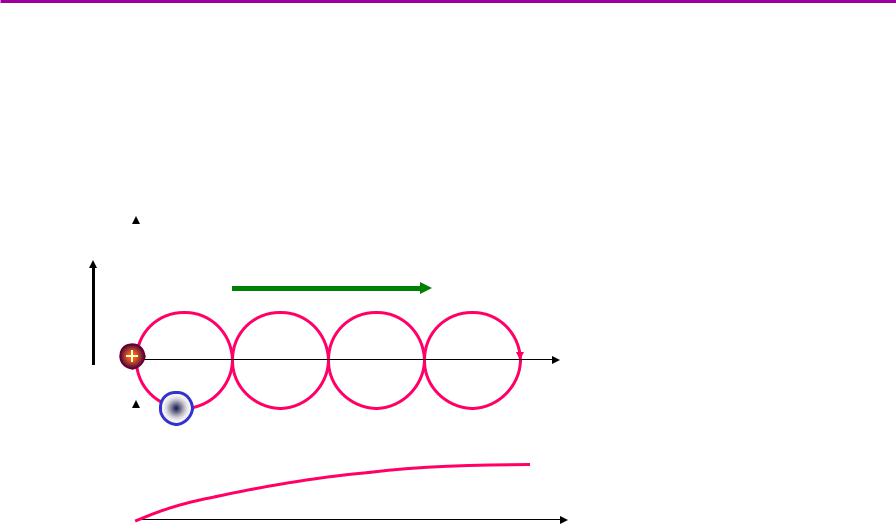
Если частица находится в циркулярно-поляризованной волне с «правильной» поляризацией, то радиус спирали растет пропорционально времени. Энергия частицы растет пропорционально квадрату времени. В результате столкновений энергия вращения переходит в тепловую.
Метод нагрева плазмы:
ЭЦР |
fce = 28·B |
[ГГц] |
ИЦР |
fci = 15·B·Z/A |
[MГц] |
 впервые ЭЦР нагрев плазмы получен в 1971 г. на токамаке ТМ-3 (Курчатовский институт)
впервые ЭЦР нагрев плазмы получен в 1971 г. на токамаке ТМ-3 (Курчатовский институт)

В.В.Поступаев * Физика плазмы, тема 8
ИсточникиСВЧ – гиротроны (λ~~ 22 мммм))
гиротрон (P ≈ 1 МВт) |
алмазное окно гиротрона |
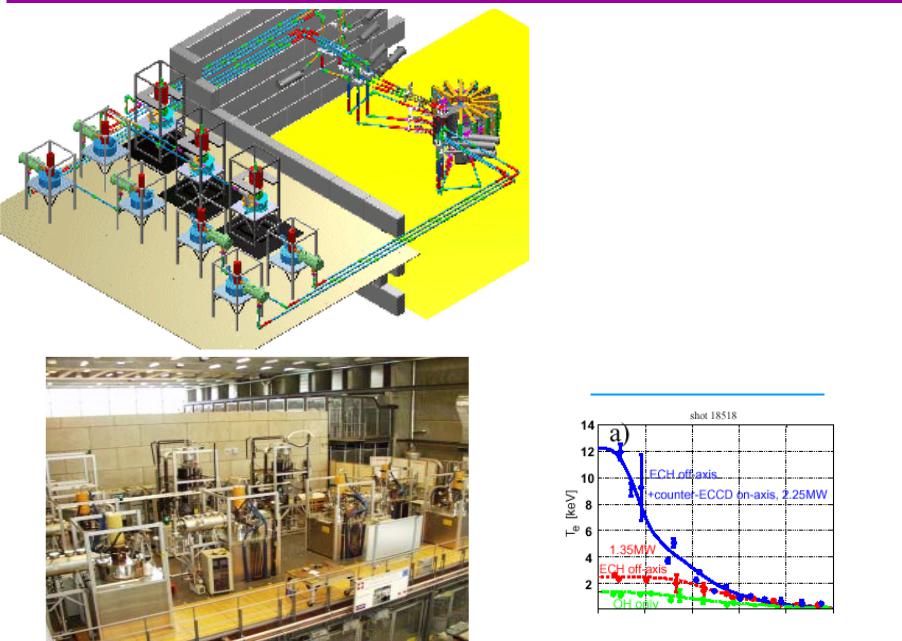
В.В.Поступаев * Физика плазмы, тема 8
ЭЦРнагревнатокамаке TCV (Швейцарияейцария))
гиротронный комплекс
 токамак
токамак
 волноводы
волноводы
 гиротроны
гиротроны
зелёным – без СВЧ нагрева синим – 2.25 МВт ЭЦРН
0 |
R |
В.В.Поступаев * Физика плазмы, тема 8
Дрейфовое приближениее
Уравнения движения частицы в электрическом и магнитном полях:
d r |
|
dυ q |
|
|
|
qB(r) |
||
|
=υ, |
|
= |
|
E + υ ×ωH |
где ωH ≡ |
|
|
dt |
dt |
m |
mc |
|||||
локальная циклотронная частота
если
то частица движется почти по окружности и можно пользоваться дрейфовым приближением (отслеживается только траектория ларморовского центра)
Координаты центра:
R ≡ r − ρ = r + |
1 |
|
|
|
|
|
|||||
ω |
H |
υ ×h(r ) |
|
||
|
|
|
|
|
|

В.В.Поступаев * Физика плазмы, тема 8
Методполучениядрейфовых уравненийравнений
движение вдоль |
электрический |
центробежный |
градиентный |
силовой линии |
дрейф |
дрейф |
дрейф |
В.В.Поступаев * Физика плазмы, тема 8
Магнитноеиэлектрическое полеполе
Скрещенное электрическое и магнитное поле
|
|
|
|
dυ |
= |
q |
E + υ ×ω |
H ] |
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
dt |
|
m |
[ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
x |
E × B |
|
|
|
|
|
E |
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
υd = c |
|
|
|
|
|
|
|
υd |
= c |
|
|
||
|
|
|
|
|
B |
|
|
|||||||
|
|
B2 |
|
|
|
«быстрое» включение |
||||||||
|
|
|
|
|
|
|
||||||||
E |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ωHτ <<1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
«медленное» включение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωHτ >>1
Дрейфовая скорость не зависит от заряда и массы частицы
В.В.Поступаев * Физика плазмы, тема 8
Понятиедрейфового движенияения
Скрещенное электрическое и магнитное поле
dυ |
= |
q |
E + υ ×ω |
H ] |
|
υd |
|
= c |
E |
|
|
||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
dt m |
[ |
|
|
B |
|||||
|
|
|
|
|
|
||||
Стандартная механика Ньютона: ускорение частицы постоянно,
направление ускорения совпадает с направлением вектора силы
F = ma
Дрейфовое движение: в магнитном поле скорость дрейфа частицы постоянна и перпендикулярна направлению приложенной силы
υd = const F
NB: вместо электрической в этом рассмотрении может быть другая сила
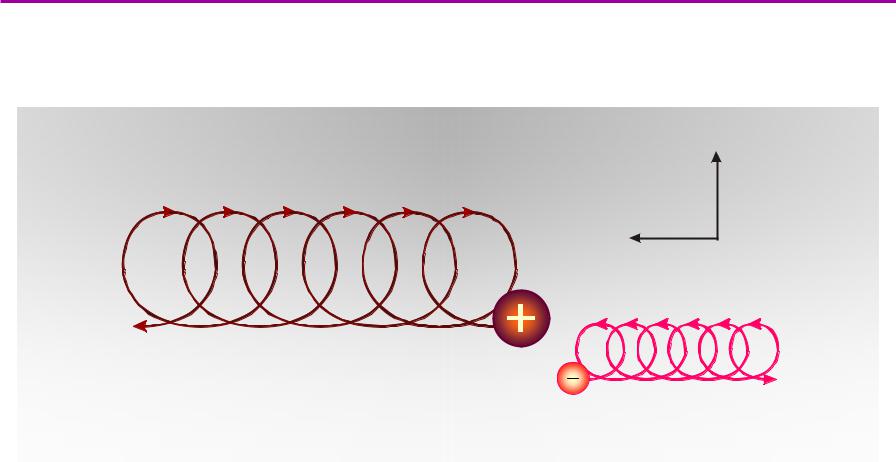
ГрадиентныйдрейфВ.В.Поступаев * Физика плазмы, тема 8
пусть магнитное поле неоднородно в пространстве (есть градиент) рассматриваем компоненту скорости, перпендикулярную к магнитному полю
сильное поле, большая кривизна |
B |
B ×B  B
B
слабое поле, малая кривизна
|
d R |
|
2 |
|
|
|
2 |
|
|
|
|
|
= |
υ |
h ×B |
= |
υ |
|
B ×B |
|
|||
|
dt |
|
2ωH |
|
|
B2 |
|
||||
|
|
2ωH B |
|
|
|
|
|
||||
Электроны и ионы дрейфуют в разные стороны

В.В.Поступаев * Физика плазмы, тема 8
Векторкривизнысиловой линииинии
пусть магнитное поле неоднородно в пространстве (есть градиент) рассматриваем продольную компоненту скорости
вектор кривизны силовых линий
производная вдоль силовой линии
h - единичный вектор магнитного поля
Так как
То
 радиус кривизны силовой линии
радиус кривизны силовой линии
