
lec_termod_kv_mech
.pdfюсовершаетдругим. Òепловой,елам.жетЕслирезервуарîïðñàìпередаваизводитм кроскопическойьработувнутреннююза счетработыýíåð- |
|||||||||
энергиейтеплового резервуара,тольктело оно |
í |
|
я раб чим телом. |
||||||
наПоп äразумев ется, |
резульататезываетсакого процесса во всех |
||||||||
единственностью результ |
|
|
ормулировк |
Томсо- |
|||||
о тальных телах не д лжно п оизойти никаких изме ений (за |
|||||||||
исключениемгии оторого |
тепловчтого резервуара, часть |
внутренней энер- |
|||||||
|
производ |
|
|
|
. |
|
|||
В ормулировкпойдетТомсона сущеñòâенноработы)акже и то, что про |
|||||||||
цесс должен быть к уговым. Процесс же, но не круговой, свя- |
|||||||||
занный с полным пр вращением |
|
работу тепла, |
|
||||||
р б чим телом от теплового резервуара, возможполученного. Пример |
|||||||||
такого |
оцесса привел Планк. Пусть в вертикальном цилин- |
||||||||
äðå ñ |
ршнем нах дится идеальный газ, а на поршне лежит |
||||||||
груз (допустим, что |
это очень мелкий песок). Цилиндр при |
||||||||
дится |
контакт с тепловым резервуаром, температура ко- |
||||||||
вот рого все время пр вышает температуру газа в цилиндре на |
|||||||||
бесконечно малую вåличину. Если теперь бесконечно |
|
||||||||
порциями разгружать поршень, то газ будет |
изотермическалыми |
||||||||
расширяться, производя работу по поднятию груза. Внутрен |
|||||||||
няя энергия идеального газа, завис |
|
только от температу- |
|||||||
ры, будет оставаться неизменной, |
ящаявсе тепло, |
|
îò |
||||||
теплового резервуара, полностью перейдет в работуполученноепод- |
|||||||||
нятию груза. Но это процесс не круг вой. Из |
ормулировки |
||||||||
Томсона следует, что оставив |
â ïîднятом положении, ни |
||||||||
каким способом нельзя привестигрузаз и поршень в исходное по- |
|||||||||
ложение, не вызвав в |
ающих телах ник |
èç |
åíåí é. |
||||||
Тем самым невозможенокруж овой |
|
|
ð öåññ, |
акихотороì произ- |
|||||
водится работа за счет энерãèè òåïëîâîãî |
резервуара, а при |
||||||||
|
|
|
32 |
|
|
|
|
|
|
круговойУсловилисьпроцесс,называтьединственнымпроцессомрезультатомТомсона которогооб ажаемыйÿâëÿ |
||||||||
ется производство работы за счет эн |
гии теплового рез р- |
|||||||
вуара. Тогда постулат сводится к утвåðждению, что процåññ |
||||||||
Томсона невозможен. |
начала, п иведенная Клаузиус м, |
|||||||
Формулировк |
||||||||
существенно тличаетсвторогоя т |
|
ðовки Томсона: "Тепл а |
||||||
не может самопроизвольно |
перехормулид ть |
тела менее нагрето- |
||||||
го к телу более нагретому". Под теплотой здесь понимается |
||||||||
внутренняя |
энергия. |
|
|
|
|
|
|
|
Посту |
Клаузиуса никоим образом не сводится к утвер- |
|||||||
ждению,латч |
при тепловом контакте двух тел теплот всегда |
|||||||
пер ходит от б лее нагретого тела к менее нагретому. Такое |
||||||||
утверждение в обще не составляет изического закона, яв- |
||||||||
ляясь |
определением того, какое из тел условились |
|
||||||
более нагретым, а какое менее наг етым. Передать внутрен |
|
|||||||
íþþ |
|
можно не тольк |
при не осредственномназыватько - |
|||||
такте,энергиюно ядом других |
способов. Наï |
|
. |
|||||
Содержание |
постулат |
Клаузиу а как разример,состоитизлучениемв о , |
||||||
что невозможно каким-либо способом |
забрать те ло от |
|
||||||
менее наг етого и передать его более нагретому |
ïритомтелаак, |
|||||||
чтобы |
ï |
де больше не |
произошло |
никаких |
изменений. (В |
|||
ор улировке К аузиуса слово "самопроизвольно им ет тот |
||||||||
ж смысл, что и словосочетание "без каких-либо изменений во |
||||||||
всех остальных те ах"). Любой воображаемый процесс, при |
||||||||
котором осуществляется передача тепла от менее нагретого |
||||||||
тела более нагретому без каких-либо изменений в окружаю |
|
|||||||
щих телах называется пр цессом Клаузиуса. И постулат сво- |
||||||||
дится к утверждению, что |
процесс Клаузиуса невозможен. |
|
||||||
Но постулат Клаузиуса не утверждает, что передача тепла
33
болееянияÅñëè æдругихнагретомудопуститьтел,становитсятопроцессы,передачавозможнойприводящиетепла от менее. Такк изменениювнагретогохолодильныхсостоòåëà |
|||||
машинах тепло ередается |
|
менее нагретых тел более на- |
|||
гретымкой процесс |
происротиворечитх дит не |
|
|
а сопровож- |
|
. Ýòî íå |
|
постулату Клаузиуса, так как |
|||
Достаточн |
просто показать,самопроизвольно,что невозможности про- |
||||
дается работ й электрического |
ðà. |
|
|||
цесса Томсона |
|
следует |
|
жность процесса Клаузиуса. |
|
Мы это доказат льство невозмоприводим, ограничившись утвер- |
|||||
ждением изической эквивалентности постулатов Планка и |
|||||
Клаузиуса. |
|
|
|
|
|
так,еедит1.12Еслиакимиз.чтобыОбратимыесостоянияв-либорезультатевостальныхспособом1висостояниекакогонеобратимыев телахисходное-либо2непроцесссостояниепроизошлолипроцессывозможноасистема1никакихвернутьпритомперехоиз-- |
||||
менений, то такой процесс называется обратимым. |
||||
|
Примером необратимого п оцесса являетс передача тепла |
|||
менее нагр тым телам. Необратимыми являютс |
также про- |
|||
öå |
получения теплоты трением, процесс расширения газа в |
|||
пустоту, процесс ди узии. |
|
|
||
|
Все квазист тические процессы обр тимы, так как состо |
|||
ят из последователь сти состояний равно есия. Если изме |
||||
нить знаки бесконечно малых приращений |
внешних п рамет- |
|||
|
и температуры на противоположные, то систем вновь |
|||
роврнется в ходное состояние; при э ом в окружающих телах |
||||
квазистатичесêèй процесс можетчастности,происх дитьякийак в прямом, |
||||
íå |
будет ник |
х изменений. В |
âñ |
круговой |
|
|
34 |
|
|
обратимомВ термодинаö êëå.ик обычно |
рассматриваются обратимые |
||||
|
в узком смысле, когда |
|
при возвращении в |
||
процессыисх дное состояние проходит ту |
системаж последовательность со- |
||||
стояний, что и в прямом процессе. |
|
||||
Подч ркнем, что деление процессов на обратимые необ |
|||||
ратимые |
относится лишь к процессам, охватывающими изо- |
||||
лированную |
целом; разделение же процессов на |
||||
равновесные |
системувновесныенер |
(или, что то же, квазистати- |
|||
ческие и неквазистатические) |
с этим не связано. |
||||
чальнечномэто1.13 |
|
ñò.емуьТеоремапроцессов,цикловразработалучаствующихКарнооккоторыеазалметодивоказываетнихвозвращаютпервонацикловтел.большоеЦиклко |
|||
ИзменениепоследовательноСади.оеЦиклсчетесостояниеКарновсюКарновпервые.сиМетод |
|
|
- |
||
âëèÿ |
на развитие термодинами и. |
|
|||
|
|
состояния системы обычно характе изуют из |
|||
менениемления трех основных параметров: температуры T , äàâ-
ризующейплощадь,граммыцессы,1834 г.соствпероткладыватьизаключеннаяизменениеавляющиеобъемаыепредложилсостоян.циклдавление,Французскийвнутри.Еслиизображатьясистемы,замкнутойпопоосиосиизикрезуординатбунаабсциссдеткривой,Бдиаграмме. представлятьКлтакойобъем,йперонхарактедиапротов- |
||||
P |
V |
|
- |
|
собой раб ту, вып лненную с стемой в |
ль ате цикла. Ес |
- |
||
ли в круговом процессе точка, изображающая состояние |
|
|||
стемы, п ремещается по часовой стрелке, то работа системы |
||||
положит льна, в противном случае отрицательна. |
|
|
||
 соответствии |
со вторым началом термодинамики тепло- |
|||
|
35 |
|
|
|

резервуара:Особое значен |
äëÿ |
èðìîх лодильникимеет. |
тепловая маши |
||||
на, у которойнагревательод нагревательдинамикио |
холодильник с посто |
||||||
ÿíí ìè температурами. азработанный Карно цикл обра- |
|||||||
тимый круговой процесс, состоящий из двух изотерм и двух |
|||||||
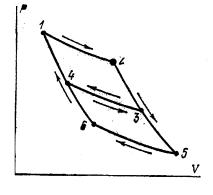
адиабат (рис. 1). |
|
Пусть |
|
нагревателя |
|||
|
|
|
|||||
èñ.1 |
|
и холодильниктемпературыравны |
T1 |
è |
T2 |
||
|
|
ло,ответственноимеятемпературу.Сначала |
|
||||
|
|
|
|
|
рабочее тесо |
||
термерабочее1-тело2.При |
|
|
|
|
T1 |
|
|
теплотыбудетэомравновесрабочееледитсвателемíымнотелоуобразомтепловой.еньшаяполучаетЗатем,расширятьсявнешнеебесконтактположительноеонечнодавление,,спопривонагремедизо--
количество Q
адиабатически1 совершает положительную работу
A
áетсате12я,конечно.В2рабочее-3точкссовемедлен2телотепловойшеíоеиемравновесноеположительнойонтактизолируетсярасширениенагревателемработыипопроисходитпрекращапоадиа--
A
внутреннейикактолькоет, энергииона достелаигн.тепловойТ мптемпературыратура телахолопридильникэтом23 запсчетада-
T
(точкТеперь,равнстемойрицательнуюавесно3)совершаетсбесконечноустжимаютанавливаютрабо яумедработатеëеннопо(т.изотермеувеличив.самаконтсистема3якт-4.внешнеесПрихолосэтомвершаетдавление,надомотси2-.
некоторое количествоAтепла34). абочее тело отдает хîлодильнику
Q
чтобыстему вмоисхжнодноебылосостоквазянèестатическим1.362Для.Состояниеэтогосжнадо4тиемвыбираетсясовершитьвернутьтак,надси-

работу A
чения 41). Температура тела при этом поднимется до зна-
T
энергияработассмотрим1.системыВ р зульнеатеизменится,акого круговогоа потомупроцессався произведеннавнутр яя
A = A + A + A + A = Q − Q
телагияизотермахсовершениеидеальногоиспользуетсявсяработы12простейшийподводимаягазаиде.23Поэтомузависитльный34случай,крабочемутолькгаз41. Таккогдаот1 кактелутемпературы,вкачествевнутренняя2.теплот рабочидеттоэнерíàãî-
V2
Z
АналогичноQ1 = A12 = P dV = νRT1 ln (V2/V1) > 0.
V1
Íà
Èç
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
другое), |
|
адиабатах 2-3 и 4-1 имеют |
|
|
|
соотношения |
|
|||||||||||
Q2 |
= |νRT2 ln (V4/V3)| |
=местоνRT2 ln (V3/V4 . |
|
|||||||||||||
T V |
γ |
1 |
= T V |
γ |
− |
1 |
T V |
γ |
1 |
= T V |
γ |
1 |
|
|||
|
− |
|
|
|
− |
|
− . |
÷òî |
||||||||
последнего следует (еслии поделить одно на |
|
|||||||||||||||
1 |
|
2 |
|
2 |
3 |
|
|
|
1 |
1 |
|
2 |
4 |
|
|
|
VV4 = VV1
альнымВитогеазомполучим,вкачествечток.рабочегоп.д3. обратимого2 тела равенцикла Карно с иде-
Q1 |
|
Q2 |
|
Q2 |
|
T2 |
|
|
знаменитепловойтую37матеоремуøèны, Каработающейíî: коэ ициентпоцик- |
||||||||
полезногоДокажемдействиятеперьη = |
− |
|
= 1 |
− Q1 |
= 1 |
− T1 |
. |
(1) |
|
Q1 |
|
|
|
|
|
||
T T
вателяшины,КмыеКарно.п.дтепловые..необратимойаитакжехолодильникарезервуары,от тепловойвидаииспользуемогонеменьшемашины,зависитк.п.дотимеющий.рабочегообратимогоустройства1 веществате2 жециклама-.
же тепловые резервуары |
, имеющие одни и |
å Для этого рассмот им два цикла C è C′ |
|
òáытьимыйличесрабочеекакциклобратимым,теплКарно.Всэтихидеальнымакциклахнеобратимымсоответственно,газом′. Первыйрезервуара.Второйииспользоватьизциклнихможетобралю--
R R
êî |
âà |
òû |
|
Q1′ |
|
|
R1 áå òñÿ |
|
|
ðàâí |
Q1 |
|
|
а резервуаðó R2 |
|||
|
|
|
оличество |
теплоты |
|
|
||
п редается совершаетсê |
|
|
|
|||||
те в цикле |
|
|
|
|
Q2 = Q2′ . Â ðåçó üòà- |
|||
работа |
C |
|
|
я работа A = Q |
Q , а в цикле C′ |
|||
ÅñëèAтеперь′ = Q′ |
обратитьQ′ . öèêë |
1 − |
2 |
|
||||
|
1 |
− |
2 |
|
|
|
|
|
обоих ц клов будет поглощатьсCя, òеплотврезультатеа выполнения |
||||||||
àðà |
è совершаться работ |
Q1′ |
−Q1 из резерву- |
|||||
R1 |
|
|
|
|
|
A′ − A = Q1′ − Q1, |
чалусостермояние |
|
резервуара |
|
|
|
|
|
|
||
R
динамики в 2ормулировкенеизменитсяТомсона.Согласнодолжновтор мубытьна - резерностью( нельзяуарапревращаяциклическибезизменениявполучитьнеетеплоту,вдругихполозабтелах),èтельнуюраемуюилиотработу,Aтеплового′ − A ≤ 0-
следователь о Q′1 ≤ Q1 è,
мы Карно Зíàêηравенства′ η, чтоотноситсядоказываеткслучаю,вторуюкогдачастьциклатеоре- |
|
тоже обратимый. ≤ |
|
В самом деле, обращением тогда |
C′ |
|
|
аналогично доказывается, что |
C′ |
обратимог |
öè ëà |
η′ |
≥ |
η. Получается,соотношечдля |
|
|
Ýòî |
|
|
||
íèÿ |
C′ |
дновременно выполняются |
- |
||
|
. Такимозначает,38образомчтополучаемсправедлива и первая |
||||
частьη′теоремыη η′ Карноη. |
|||||
≥ |
≤ |
|
|
|
|

|
|
Q1 |
|
Q2 |
|
T1 |
|
T2 |
|
Q1 |
Q2 |
|
|
|
ствияногошин,Коэродажидеальнойηициентпотерьесли= − |
|
|
≤ |
|
− |
|
, |
→ T1 − T2 |
≤ |
0. |
(2) |
|||
|
|
|
T1 |
|
||||||||||
|
|
Q1 |
|
|
|
|
|
|
||||||
|
|
втепловойполезногоихменьше,основемашинычемдлежитйствиякоэвозмоцикл.ПреальнèöñëКарно,иентеднийûõполеявляетсятепловыхиз-çногоаразличпредейма- |
||||||||||||
дельным значением, определяя |
|
жные границы совер |
||||||||||||
шенствов ния. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема |
Карно ясно показывает, что энергия характери- |
|||||||||||||
зуется не только количественно, но и качест енно. Любая |
||||||||||||||
периодически действующая машина может |
превратить |
â ðà- |
||||||||||||
боту только часть |
|
пловой (внутренней) энергии тела. Ч |
||||||||||||
âûøå |
|
|
тела, тем выше качество запасенной |
íåì |
||||||||||
|
температураак как большая |
часть |
|
у этого тела тепловой |
||||||||||
энергии может быть превращенавзятойаб ту. Всякий естествен- |
||||||||||||||
но идущий необратимый процесс пðиводит к |
|
|
|
|||||||||||
тором качество энергии |
|
|
|
|
я, возможобесцениваниютольк при |
|||||||||
энергии в указанном выше смысле. Обратный процесс, |
ê - |
|||||||||||||
наличии другого процесса,повышаетскотором качество энергии умень |
||||||||||||||
|
я (энергия обесценивается). Этот другой |
процесс Кла |
||||||||||||
шаетсузиу назвал компенсирующим процессом или, короче, ком- |
||||||||||||||
пенсацией. Например, можно |
тнять тепло |
|
õîëî |
à |
||||||||||
передать его нагревателю. Но для этого необх димдильникомпен- |
||||||||||||||
сирующий |
процесс, скажем, производство работы. |
|
||||||||||||
|
|
|
|
|
|
|
39 |
|
|
|
|
|
|
|

|
1. Найти к.п. . цикла состоящего из двух изохор и двух изо- |
||||||||||||||||
бар, полагая что р |
очим веществом является деальный газ |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
циклов, |
|
|
|
|
||
си показателемобъемОтвет:меняютсяадиабатыв два γðàçà= 1. , 4. В пределах цèкла давление |
|||||||||||||||||
тычим2. веществомНайтиη =ê.ï(γ. − 1)/(2γ + 1) 0 105 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
являетсд. сл дующихя идеальный газпредполспоказàгая,тел ратурамичтоадиàáàî- |
||||||||||
|
γ =Клайперона);1, 4: цикл состоит из двух изотерм с темпå |
|
|||||||||||||||
(öèêë |
|
( |
T2 |
> T1 |
|
двух изохорсостоитобъемами изобар, |
V2 > V1 |
||||||||||
T1 |
T2 |
|
|
á) öèêë |
|
èç äâóõ |
V1 |
V2 |
|||||||||
í |
ÿìè |
|
|
|
|
|
|
|
|
|
|
с давле- |
|||||
îò |
|
|
P |
|
Pèç P |
|
> P |
|
|
|
|
|
|
|
|||
|
состоит |
2 |
( двух адиа) ат,двухизобарыадиабатсизменением(циклДжоуля);объемав) |
||||||||||||||
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
|
|
|
|
||
|
V1 |
доДизеля)изо оры с объемом |
V3 |
, причем |
V1 |
< V2 < V3 |
|||||||||||
|
|
|
V2 |
|
|
|
|
|
|
|
|
|
|||||
(öèêë |
|
|
Ответ:. а) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
á) |
|
|
η = |
|
(γ − 1)(T2 − T1) ln (V2/V1) |
; |
|
|||||
|
|
|
|
|
|
|
|
|
|
T2 − T1 + (γ − 1)T2 ln (V2/V1) |
|
||||||
â) η = 1 − (P1/P2)(γ−1)/γ ;
1ЛЕКЦИЯ.14 4
=η = 1 − 1 · (V2/V3)γ − (V1/V3)γ .
γ(V2/V3) − (V1/V3)
ПустьзависетьИз. теоремыТермодинамическаятолькоКарнооттемпслåдует,ратурчтошкаланагревателяк.п.дтемператур. циклахолоКарнодильникможет.
t è t
гревателя,1 измеренны2 эмпирич скакимиетемпера-либо термометромуры холодильник.Тогда на-
Q1 − Q2
η ≡ 40 = f (t1, t2), Q1
скихотлыпредложившийществаустройстватемпературf (темперt.,Ýòèìt ) турмашиныобстоятельством. применитьВведем. Вид КарноэтойвместоциклункцииотКарновоспользовалсиспользуемогосовершеннодля построениярабочегоВне. Томсон,зависитшкаве-
1 2
сальную ункцию температур η(t1, t2) более простую универ
|
Q |
|
1 |
|
ϕ(t1, t2) = |
1 |
=Äëÿункцииопределåíèÿ. общего вида |
||
Q2 |
||||
|
1 |
− η(t1, t2) |
||
èñ.2 |
ческимитепловыхтемпературезϕ(t ,âót ) ðàвозьмеммисэмпиритри- |
||
|
1 |
2 |
|
изображенные на рис. 1. |
Будемкачествеников,соответствиметьпроведем |
|
t1, t2, t3 |
|
|
|
èëüõâ- |
|
соотношенияннотри.ИспользуяцклахолодКарно |
||
|
нагревателей |
|
|
Q1 |
ϕполучим(t , t ) |
Q2 |
= ϕ(t , t ). |
|
||
Исключив отсюäà = |
|
(1) |
||||
|
||||||
|
1 |
2 |
|
вместе, |
3 |
|
Q2 |
|
|
Q3 |
|
|
|
Q2, |
|
|
|
|
|
|
|
|
Q1 |
|
|
|
|
|
|
номуНо этициклудва Карно,цикла, îáтакъединенные=êàêϕ(tâ,îðàÿt )ϕ(tизотермаt ) эквивалентныстемпературойд- |
||||||||
|
|
Q3 |
1 |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
визпрассмотренияивположных. |
||||||
можетпроходитсябытьисключенадважды |
|
|
|
|
Следовательнонаправ ениях и |
|||
|
Q1 |
|
|
|
|
|
ϕ(t1, t3) |
|
|
|
= ϕ(t1, t3), → 41ϕ(t1, t2) = |
|
. |
||||
|
Q3 |
ϕ(t2, t3) |
||||||
