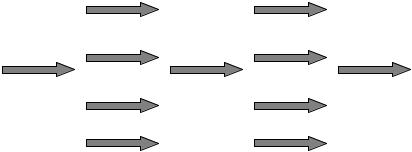
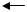Join (ОБЪЕДИНЕНИЕ): когда потоки в параллельной области завершаются, они синхронизируются и закрываются, оставляя только главный поток (рис. 8.10).
F J F J
master |
|
|
|
master |
|
|
|
master |
thread |
|
|
|
thread |
|
|
|
thread |
|
|
|
|
|
|
|
|
|
Рис. 8.10. Модель распараллеливания в OpenMP
Директивой, задающей параллельный блок, является директива:
#pragma omp parallel [clause clause ...] { . . .
}
Основными директивами, которые распределяют работу по параллельным процессам, являются:
#pragma omp for [clause clause ...] { . . .
}
и
#pragma omp sections [clause clause ...] { . . .
#pragma omp section { . . .
}
}
Директива for распараллеливает циклы. Витки циклов выполняются по одному и тому же алгоритму, т.е. директива #pragma omp for использует SPMD-модель вычислений. Но
SPMD-модель не что иное, как распараллеливание по данным.
Т.е. каждый параллельно исполняемый процесс обрабатывает некоторую часть назначенных ему данных аналогично, как и в MPI, но разница только в том, что здесь данные расположены в общей памяти.
Директива #pragma omp sections как правило применяется для параллельного выполнения некоторых участков программы с разными кодами, т.е. эта директива использует MPMD-модель вычислений.
8.3.1. Умножение матрицы на матрицу. Умножение матрицы на вектор и матрицы на матрицу являются, как было сказано, базовыми макрооперациями для многих задач линейной алгебры, например итерационных методов решения систем линейных уравнений и т. п. Поэтому приведенный алгоритм можно рассматривать как фрагмент в алгоритмах других задач. В отличие от программирования в MPI здесь рассматривается только одна схема распараллеливания алгоритма – это распараллеливание циклов (SPMD-модель вычислений). Такая схема определяется наличием общей памяти и независимостью выполнения циклов.
Заданы две исходные матрицы A и B. Вычисляется произведение C = А х B, где А - матрица n1 х n2, и B - матрица n2 х n3. Матрица результатов C имеет размер n1 х n3. Исходные матрицы определены в общей памяти. Но распараллеливание циклов – это распараллеливание по данным. Т.е. каждый параллельно исполняемый процесс обрабатывает некоторую часть назначенных ему данных аналогично, как и в MPI, но разница только в том, что здесь данные расположены в общей памяти. Распараллеливается внешний цикл, переменная, которого указывает на строки матриц A и C. Поэтому матрицы A и C можно представить условно разрезанными, как показано на рис. 3.2, на p горизонтальных полос (p – количество
параллельных процессов). Матрица B не разрезана, т.к. столбцы этой матрицы указываются переменной внутреннего цикла, которые в данном случае не распараллеливается, т.е. все столбцы обрабатываются каждым параллельным процессом.
Рис. 8.11. Умножение матриц. Полосами указаны части исходных данных, обрабатываемых разными процессами (p=4).
Текст программы, реализующий алгоритм, приведен ниже.
/* Пример программы на языке С (с OpenMP) произведения двух матриц. */ /* Здесь в примере исходные матрицы генерируются в программе */
#include<stdio.h>
#include<sys/time.h>
#include<omp.h>
#define M 1000 #define N 1000
/* Задаем исходные матрицы. */
double A[N][M], B[N][M], C[N][M];
int main()
{int i, j, v, nr; int size, rank; long int dt1;
struct timeval tv1, tv2;
/* Генерация исходных матриц A и B, полосы C обнуляются */
for(i = 0; i < N; i++)
{for(j = 0; j < M; j++)
{A[i][j] = 3.0; B[j][i] = 2.0; C[i][j] = 0.0;
}
}
/* Заказываем количество параллельных процессов */ omp_set_num_threads(4);
/* Задаем параллельный блок из (4-х) процессов. Номер процесса (rank) должен быть обязательно приватным во всех процессах*/
#pragma omp parallel private(rank,size,i)
{ /* Каждый процесс узнает количество процессов и свой номер в стартовавшем приложении */
size = omp_get_num_threads(); rank = omp_get_thread_num(); nr = M/size;
gettimeofday(&tv1, NULL);
/* Задание работ. Распределяем витки внешнего цикла по процессам и каждый процесс перемножает свои полосы матрицы A */
#pragma omp for schedule(static,nr) private(j,v)\\ nowait
for(i = 0; i < N; i++)
{for(j = 0; j < N; j++)
{for(v = 0; v < M; v++)
C[i][j] += A[i][v] * B[v][j];
}
}
/* Каждый процесс выводит время решения */
gettimeofday(&tv2, NULL);
dt1 = (tv2.tv_sec - tv1.tv_sec) * 1000000 + tv2.tv_usec - tv1.tv_usec;
printf(" rank=%d Time=%ld\n",rank,dt1);
} /* Конец параллельного блока */
}
8.3.2.Параллельный алгоритм решения СЛАУ методом Гаусса
Требуется найти решение системы линейных алгебраических уравнений:
Ax = f
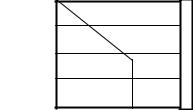
Рассматриваемая здесь схема распараллеливания алгоритма, как и в предыдущей задаче, – это распараллеливание циклов. Это значит, что каждому процессу назначается для обработки полоса строк матрицы коэффициентов (см. рис. 8.12). Но при распараллеливании этого алгоритма в OpenMP есть особенности, существенно отличающие его от предыдущего алгоритма умножения матриц. При прямом ходе в данном алгоритме выбор строки (назовем ее текущей), которая в начале делится на диагональный коэффициент, а затем вычитается из всех нижележащих строк, является последовательным процессом, который начинается с нулевой строки и заканчивается последней. И процесс выбора текущей строки последовательно пересекает все полосы, обрабатываемые разными процессами. Выше лежащие строки от текущей обрабатывать не нужно. В обратном ходе наоборот. Поэтому здесь в параллельном блоке автоматическое распределение витков цикла с помощью директивы #pragma omp for не подходит. В данном алгоритме в параллельном блоке применено "ручное" распределение работ по параллельным процессам. При этом каждый параллельный процесс динамически вычисляет номера "своих" строк для их обработки на каждом витке циклов (прямого и обратного) (см. рис. 8.12). На рис. 8.12 схематично показан текущий момент приведения матрицы коэффициентов к диагональному виду (прямой ход). На этом рисунке ломаная линия обозначает текущую границу, слева от которой стоят
нулевые элементы, с права – не нулевые элементы. Т.е. нулевой и первый процессы свои полосы уже привели к диагональному виду, второй процесс приводит к диагональному виду только часть своих строк, третий процесс приводит к диагональному виду все свои строки. Деление элементов текущей строки на диагональный коэффициент осуществляет один процесс - master. Поэтому доступ к текущей строке другими параллельными процессами, для вычитания из "своих" строк, синхронизирован.
0
1
2 
3 
АF
Рис. 8.12. Решение СЛАУ методом Гаусса. Полосами указаны части исходных данных, обрабатываемых разными процессами
(p=4).
Текст программы, реализующий алгоритм, приведен ниже.
/* Пример программы на языке С (с OpenMP) решения СЛАУ методом Гаусса. */ /* Здесь в примере исходная матрица генерируется в программе */
#include<omp.h>
#include<sys/time.h>
#include<stdio.h>
#define M 1000 #define N 1000
/* Задаем исходную матрицу коэффициентов. */
static double MA[N][M+1], MAD, R;
int main()
{int size, rank, i, j, v, k, Np, uk, dn, dk; struct timeval tv1, tv2, tv3, tv4;
long int dt1,dt2; /* Для засечения времени */
/* Генерация исходной матрицы МA */
for(i = 0; i < N; i++)
{for(j = 0; j < M; j++)
{if(i == j)
MA[i][j] = 2.0; else
MA[i][j] = 1.0;
}
MA[i][M] = 1.0*(M)+1.0;
}
/* Заказываем количество параллельных процессов
*/
omp_set_num_threads(4);
/* Задаем параллельный блок из (4-х) процессов. Перечисленные переменные должны быть обязательно приватным во всех процессах*/
#pragma omp parallel private(i,j,k,rank,Np,uk,dn,dk,tv1,tv2)
{
size = omp_get_num_threads(); Np = M/size;
rank = omp_get_thread_num(); uk = Np * rank;
gettimeofday(&tv1, NULL);
/* Прямой ход */
for(k = 0; k < M; k++)
{
/* На каждом шаге цикла вычисляем полосы строк (dn-начало, dk-конец полосы), обрабатываемых каждым процессом */
dn = (uk * (k < uk)) + ((k + 1) * (k >=
uk));
dk = uk + Np - 1;
/* Синронизация процессов */
#pragma omp barrier
/* Деление на коэффициент элементов текущей строки процессом master */
#pragma omp master
{MAD = 1.0/MA[k][k]; for(j = M; j >= k; j--)
MA[k][j] *= MAD;
}
/* Синронизация процессов для того что бы master успел обработать сроку */
#pragma omp barrier
/* Обработка строк параллельными процессами */
for(i = dn; i <= dk; i++) { for(j = M; j >= k; j--)
MA[i][j] -= MA[i][k]*MA[k][j];
}
}
/* Обратный ход */
uk = (M - 1 - Np * (size - rank - 1)); for(k = M-1; k >= 0; k--)
{
/* На каждом шаге цикла вычисляем полосы строк (dn-начало, dk-конец полосы), обрабатываемых каждым процессом */
dn = ((uk * (k > uk)) + ((k-1) * (k <= uk)));
dk = uk - Np + 1;
/* Синронизация процессов, т.к. получение корней – процесс последовательный */
#pragma omp barrier
/* Обработка строк параллельными процессами */
for(i = dn; i >= dk; i--) MA[i][M] -= MA[k][M]*MA[i][k];
}
/* Каждый процесс выводит время решения */
gettimeofday(&tv2, NULL);
dt1 = (tv2.tv_sec - tv1.tv_sec)*1000000+ tv2.tv_usec-tv1.tv_usec;
printf(" rank1= %d Time= %ld\n",rank,dt1); printf(" rank1(0)= %d %f %f %f %f\n",rank,
MA[rank][M],MA[rank+1][M],
MA[rank+2][M],MA[rank+3][M]);
} /* Конец параллельного блока */
return(0);
}
8.3.3. Параллельный алгоритм решения СЛАУ методом сопряженных градиентов
Все формулы, по которым решается данная задача, приведены ранее. Рассматриваемая здесь схема распараллеливания алгоритма – распараллеливание циклов (SPMD-модель вычислений), т.е. распараллеливание по данным. Каждый параллельно исполняемый процесс обрабатывает некоторую часть назначенных ему данных аналогично, как и в MPI. Распараллеливается внешний цикл, переменная, которого указывает на строки матрицы A и элементы векторов F, X, R, и Z. Поэтому эти данные можно представить условно разрезанными, как показано на рис. 8.13, на p горизонтальных полос (p – количество параллельных процессов). На рис. 8.13 схематично показаны исходные данные задачи. Полосами указаны части исходных данных, параллельно обрабатываемых разными процессами. Такая схема определяется наличием общей памяти и независимостью выполнения циклов.
0
1
2 
3 
А F X R Z
Рис. 8.13. Решение СЛАУ методом Сопряженных градиентов. Полосами указаны части исходных данных, обрабатываемых разными процессами (p=4).
Текст программы, реализующий алгоритм, приведен ниже.