
- •Лекции по курсу «Кинетика жидкофазных реакций»
- •Раздел I. Введение в кинетику жидкофазных реакций. Структура жидкости
- •Тема 1. Диффузионный и кинетический контроль в кинетике жидкофазных реакций
- •Вязкость. Уравнение Стокса – Эйнштейна. Численная оценка kD.
- •Оценка частоты столкновений в жидкости
- •Тема 2. Представление о структуре жидкости
- •Движение в квазикристаллической среде
- •Раздел II. Межмолекулярные взаимодействия и сольватация
- •Тема 3. Парные электростатические взаимодействия
- •Напряженность поля диполя (f):
- •Энергия взаимодействия зарядов
- •Энергия взаимодействия системы зарядов во внешнем поле
- •Индукционное взаимодействие
- •Дисперсионное взаимодействие
- •Донорно-акцепторные (д-а) комплексы и водородная связь
- •Тема 4. Континуальные модели взаимодействия растворенной молекулы с растворителем Сольватация ионов
- •Уравнение Борна-Бьеррума (4.2)
- •Теория Дебая – Хюккеля
- •Раздел 3. Диффузионно – контролируемые реакции (дкр)
- •Тема 5. Дкр в рамках теории Смолуховского
- •Граничное условие 3-рода
- •Уравнение Смолуховского для вероятностей
- •Тема 6. Учет взаимодействия реагентов в уравнении Смолуховского
- •Тема 7. Геминальная рекомбинация
- •Тема 8. Учет анизотропии реагентов
- •Тема 9. Дкр с дальнодействием
- •Вывод уравнения Штерн – Фольмера
- •Перенос энергии в жидких растворах
- •Раздел IV. Кинетически-контролируемые реакции
- •Тема 10. Кинетически-контролируемые реакции в рамках теории активированного комплекса (так)
- •Характерные времена релаксационных процессов в растворителях
- •Раздел V. Влияние давления на скорость химических реакций
- •Кинетически контролируемые реакции
- •Раздел VI. Элементы квантовой теории химических реакций. Перенос электрона
- •Тема 12. Элементы квантовой теории химических реакций
- •Туннельные реакции
- •Усреднение вероятности реакции по ансамблю
Теория Дебая – Хюккеля
Рассмотрим свободную энергию иона в
среде электролита:
![]() ,
гдеf - коэффициент
активности. В данной записи,
,
гдеf - коэффициент
активности. В данной записи,![]() - это изменение химического потенциала
при переходе 1 моля вещества из стандартного
раствора в исследуемый.
- это изменение химического потенциала
при переходе 1 моля вещества из стандартного
раствора в исследуемый.
Предположение:Вокруг любого иона
в электролите существует сфера ионов
со статистическим распределением
зарядов (ионная атмосфера). Ее толщина
(1/):
![]() (4.5);где
(4.5);где
![]() -
ионная сила раствора,ci
иzi– концентрация и зарядi-го
реагента, соответственно.
-
ионная сила раствора,ci
иzi– концентрация и зарядi-го
реагента, соответственно.
Вывод формулы (3.15) основан на применении нескольких уравнений неразрывности
![]() (Уравнение Пуассона)
(Уравнение Пуассона)
Здесь
![]() -
плотность некомпенсированных зарядов.
-
плотность некомпенсированных зарядов.
Считаем, что у нас есть распределение Максвелла – Больцмана:

Здесь мы учли, что
![]() .
Тогда получим, что
.
Тогда получим, что![]() (если
концентрация в моль/л).
(если
концентрация в моль/л).
Оценим толщину ионной атмосферы. Пусть у нас 1:1 электролит с ионной силой 10-3 М.
![]()
Т.е. при ионной силе 0.001 толщина равна 100 А, а при I = 0.1 толщина равна 10 А.
Запишем теперь уравнение Пуассонав сферических координатах:![]() .
.
Решение этого уравнения имеет вид
![]() (4.6). Проверим это:
(4.6). Проверим это:
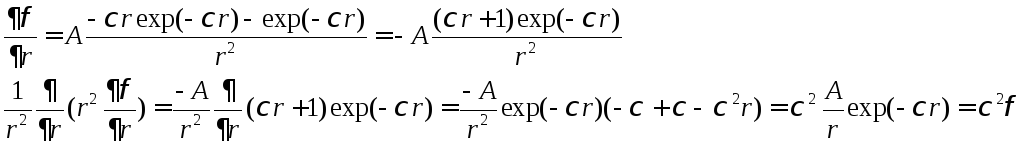
Что и т.д.
К онстантуАлегко найти в том случае, когдаI
= Iдобавки(т.е. при постоянной внешней ионной
силе). При0 должен
получаться потенциал точечного заряда
онстантуАлегко найти в том случае, когдаI
= Iдобавки(т.е. при постоянной внешней ионной
силе). При0 должен
получаться потенциал точечного заряда![]() .
Отсюда
.
Отсюда![]() (4.7)
(4.7)
Посчитаем теперь
![]() .
Рассмотрим работу по созданию ионной
атмосферы:
.
Рассмотрим работу по созданию ионной
атмосферы:

![]() ,А
- работа по заряжению ионной атмосферы.
,А
- работа по заряжению ионной атмосферы.
Вспомним, что
![]() т.е.
т.е.![]() . Тогда:
. Тогда:
![]()
Считаем, что ионы точечные и интегрируем от нуля до бесконечности:
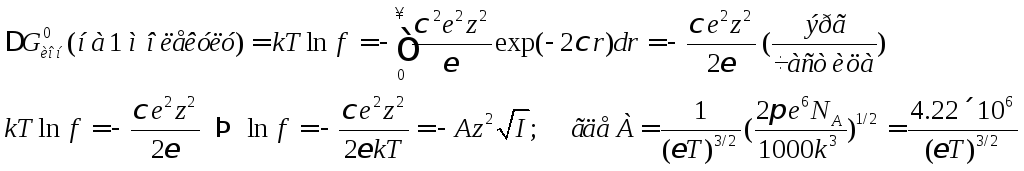
Запишем популярное выражение для
электролита 1:1 при 250С в воде:![]() .
(4.8) Это выражение еще называют предельным
законом Дебая – Хюккеля.
.
(4.8) Это выражение еще называют предельным
законом Дебая – Хюккеля.
![]()
Данное выражение хорошо работает при I< 0.001. При более высоких ионных силах надо вводить поправки.
Поправка №1. Снимаем условие о малости
радиуса иона:
![]() (4.9), гдеа – расстояние максимального
сближения ионов. Формула (4.9) получается
при интегрировании не от нуля, а от
конечного размераадо бесконечности.
Тогда:
(4.9), гдеа – расстояние максимального
сближения ионов. Формула (4.9) получается
при интегрировании не от нуля, а от
конечного размераадо бесконечности.
Тогда:
![]()
При высоких ионных силах вводится дополнительная поправка №2:
![]() ,
где С – эмпирическая константа
,
где С – эмпирическая константа
Недостатки теории Дебая – Хюккеля:
1. При решении уравнения Пуассона мы предполагали наличие Максвелл-Больцмановского распределения для зарядов, что вряд ли имеет место в реальности.
2. Взаимодействие между частицами определяется не только кулоновскими силой, но и Ван-дер-ваальсовыми силами и/или специфическими взаимодействиями.
3. Теория не работает в условиях, когда вещество плохо диссоциирует. (соли в неполярных растворителях).
Модель Онзагера – Бетчера(Сольватация дипольной молекулы)
В среде молекула растворенного вещества находится под воздействием всей совокупности окружающих молекул растворителя. В первом приближении можно считать, что полная энергия взаимодействия есть сумма парных взаимодействий:
![]()
В модели О-Бпредполагается, что
среда – это сплошной диэлектрический
континуум. В этой среде рассматривается
частица размеромаи дипольным
моментом![]() ,
равным:
,
равным:
![]()

![]() –
собственный дипольный момент,
–
собственный дипольный момент,![]() -
поле,
-
поле,
появляющееся за счет поляризуемости
среды внесенным диполем,
![]() -
-
наведенный дипольный момент.
![]()
![]() -энергия,
затрачиваемая на создание полости в
растворителе, в первом приближении не
зависит от свойств молекулы, а определяется
только размером полости и свойствами
среды.
-энергия,
затрачиваемая на создание полости в
растворителе, в первом приближении не
зависит от свойств молекулы, а определяется
только размером полости и свойствами
среды.
Для вкладов ориентационных и индукционных взаимодействий в энергию сольватации можно написать следующее выражение:
![]() (4.10)
(4.10)
(Энергия растяжения) (Энергия в-я диполя с полем) (Энергия поляризации среды полем)
Откуда берется первое слагаемое? Мы растягиваем диполь на некоторое расстояние Х:
![]()
Формулу (3.20) можно переписать в другом виде:
![]() (4.11)
(4.11)
Чему равно
![]() ?
Было показано, что в сферической полости
в сплошной среде диэлектрика:
?
Было показано, что в сферической полости
в сплошной среде диэлектрика:![]()
Частный случай – известная формула
Кирквуда:![]()
Найдем теперь
![]() ,
используя формулу Лондона:
,
используя формулу Лондона:![]() .
Рассчитаем энергию дисперсионного
взаимодействия молекулы с молекулами
растворителя, входящими в шаровой слой
радиусаR и толщиныdR(объемdV):
.
Рассчитаем энергию дисперсионного
взаимодействия молекулы с молекулами
растворителя, входящими в шаровой слой
радиусаR и толщиныdR(объемdV):
![]() ,
,![]() -
число молекул растворителя в шаровом
слое объемаdV= 4R2dR.
Подставим и проинтегрируем:
-
число молекул растворителя в шаровом
слое объемаdV= 4R2dR.
Подставим и проинтегрируем:
![]() .
Часто принимают, что
.
Часто принимают, что![]() ,
тогда:
,
тогда:
![]() .
Если мы теперь суммируем все сольватационные
слагаемые:
.
Если мы теперь суммируем все сольватационные
слагаемые:
![]() (4.12)
(4.12)
Оценим теперь вклад каждого из трех слагаемых в свободную энергию сольватации, считая, что a = 2 А, = 10A3/молекула,I= 10 эВ,= 2 Дб,= 5,n2= 2.

