
- •Лекции по курсу «Кинетика жидкофазных реакций»
- •Раздел I. Введение в кинетику жидкофазных реакций. Структура жидкости
- •Тема 1. Диффузионный и кинетический контроль в кинетике жидкофазных реакций
- •Вязкость. Уравнение Стокса – Эйнштейна. Численная оценка kD.
- •Оценка частоты столкновений в жидкости
- •Тема 2. Представление о структуре жидкости
- •Движение в квазикристаллической среде
- •Раздел II. Межмолекулярные взаимодействия и сольватация
- •Тема 3. Парные электростатические взаимодействия
- •Напряженность поля диполя (f):
- •Энергия взаимодействия зарядов
- •Энергия взаимодействия системы зарядов во внешнем поле
- •Индукционное взаимодействие
- •Дисперсионное взаимодействие
- •Донорно-акцепторные (д-а) комплексы и водородная связь
- •Тема 4. Континуальные модели взаимодействия растворенной молекулы с растворителем Сольватация ионов
- •Уравнение Борна-Бьеррума (4.2)
- •Теория Дебая – Хюккеля
- •Раздел 3. Диффузионно – контролируемые реакции (дкр)
- •Тема 5. Дкр в рамках теории Смолуховского
- •Граничное условие 3-рода
- •Уравнение Смолуховского для вероятностей
- •Тема 6. Учет взаимодействия реагентов в уравнении Смолуховского
- •Тема 7. Геминальная рекомбинация
- •Тема 8. Учет анизотропии реагентов
- •Тема 9. Дкр с дальнодействием
- •Вывод уравнения Штерн – Фольмера
- •Перенос энергии в жидких растворах
- •Раздел IV. Кинетически-контролируемые реакции
- •Тема 10. Кинетически-контролируемые реакции в рамках теории активированного комплекса (так)
- •Характерные времена релаксационных процессов в растворителях
- •Раздел V. Влияние давления на скорость химических реакций
- •Кинетически контролируемые реакции
- •Раздел VI. Элементы квантовой теории химических реакций. Перенос электрона
- •Тема 12. Элементы квантовой теории химических реакций
- •Туннельные реакции
- •Усреднение вероятности реакции по ансамблю
Раздел VI. Элементы квантовой теории химических реакций. Перенос электрона
Тема 12. Элементы квантовой теории химических реакций
До этого мы рассматривали «классические
реакции» - рассчитывали константы
скорости реакций по теории переходного
состояния, рассматривая движение по
ППЭ. При этом полагалось, что энергия
системы Ебольше высоты потенциального
барьера:![]() .
Однако, существуют квантовые эффекты
в химических реакциях, которые протекают
при энергиях ниже барьера:
.
Однако, существуют квантовые эффекты
в химических реакциях, которые протекают
при энергиях ниже барьера:
Туннелирование электрона и ядер 2) Перенос электрона
Задача: рассмотреть общие принципы квантово-химического подхода к определению скоростей химических реакций.
Рассмотрим систему из Nчастиц. Данная система описывается
волновой функцией![]() .
Величина
.
Величина![]() -
вероятность нахождения системы в момент
времениtвблизи
точек пространстваr1
… rN.
В стационарных условиях эта вероятность
не зависит отtи
-
вероятность нахождения системы в момент
времениtвблизи
точек пространстваr1
… rN.
В стационарных условиях эта вероятность
не зависит отtи
![]()
Где Е ищется из решения уравнения Шредингера для стационарной функции:
![]()
Нестационарное уравнение Шредингера:
![]()
Процесс элементарного химического акта можно разбить на три стадии:
Входной канал – изолированные реагенты в среде,
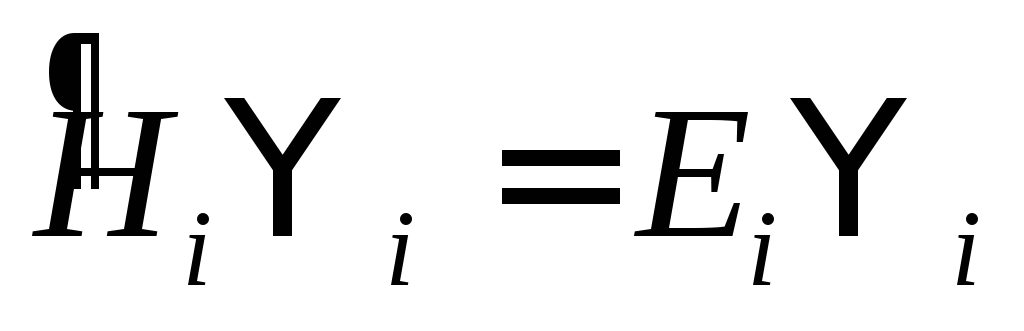
Зона реакции, есть V – взаимодействие, нестационарная волновая функция.
Выходной канал – изолированные продукты в среде,

Если бы можно было решить нестационарную
задачу для 2 стадии, то можно было бы
определить, с какой вероятностью система,
описываемая в начальном канале волновой
функцией
![]() ,
оказывается в выходном канале в состоянии
,
оказывается в выходном канале в состоянии![]() .
Однако, точные решения получаются только
в ограниченном числе случаев. Нужно
вводить упрощения даже для нахождения
стационарных волновых функций.
.
Однако, точные решения получаются только
в ограниченном числе случаев. Нужно
вводить упрощения даже для нахождения
стационарных волновых функций.
1) Одноэлектронное приближение:можно ввести одноэлектронную функцию, а межэлектронное взаимодействие свести к эффективному потенциалу.
2) Приближение Борна – Оппенгеймера
(адиабатическое): электрон всегда
успевает подстраиваться под движение
ядер. Это позволяет разделить движения
электронов и ядер и строить волновые
функции электронов при неподвижных
ядрах:![]() .
.
Причем r(электроны) – динамические переменные,Q(ядра) – параметры. Решение задачи в рамках приближения Б-О дает адиабатические волновые функции.
Полную волновую функцию системы можно разложить в ряд по адиабатическим функциям:
![]()
Простейшее приближение – учесть только
первый член этого ряда:
![]() .
Где
.
Где![]() - адиабатическая волновая функция
электронов,
- адиабатическая волновая функция
электронов,![]() -
ядерная волновая функция, полученная
при решении уравнения Шредингера для
ядерных координат:
-
ядерная волновая функция, полученная
при решении уравнения Шредингера для
ядерных координат:
![]()
Здесь
![]() - полная электронная энергия, в которую
входит усредненная по электронному
состоянию энергия межэлектронного
отталкивания, взаимодействия электронов
с ядрами, кинетическая энергия электронов,
межядерное отталкивание.
- полная электронная энергия, в которую
входит усредненная по электронному
состоянию энергия межэлектронного
отталкивания, взаимодействия электронов
с ядрами, кинетическая энергия электронов,
межядерное отталкивание.
Так как адиабатические волновые функции являются приближенными, то они не ортогональны друг к другу.
П

Так как в входном и выходном каналах
взаимодействие между частицами
отсутствует, то можно в адиабатическом
приближении найти термы начального
![]() и конечного
и конечного![]() каналов. Причина реакции – взаимодействие
реагентов под действием оператораVi,
переводящего начальную волновую функциюiв конечнуюf,
при изменении соответствующей координаты
сQi0наQf0.
Взаимодействие приводит к двум эффектам:
каналов. Причина реакции – взаимодействие
реагентов под действием оператораVi,
переводящего начальную волновую функциюiв конечнуюf,
при изменении соответствующей координаты
сQi0наQf0.
Взаимодействие приводит к двум эффектам:
(1) Изменение энергии взаимодействия
без существенного распределения
электронной плотности внутри реагентов.
Определяется кулоновским взаимодействием
и приводит к сдвигу энергии термов:
![]() .
Эти величины включают в потенциальную
энергию начального и конечного каналов:
.
Эти величины включают в потенциальную
энергию начального и конечного каналов:![]() .
.
(2) Появление обменного взаимодействия
![]() - которое и приводит к перестройке
электронного состояния и переходу изiвf.
- которое и приводит к перестройке
электронного состояния и переходу изiвf.
Переход из iвfвозможен только при примерном равенстве электронных энергий этих состояний. Если бы в процессе сильно менялась электронная энергия, то в силу закона сохранения, должна был меняться и кинетическая энергия ядер. Причем это изменение должно было происходить за время электронной перестройки, которое в силу адиабатического приближения существенно меньше, чем время движения ядер.
Принцип Франка – Кондона: Переход осуществляется только в окрестности точки пересечения термов, где выполняется равенство электронных энергий начального и конечных состояний. Окрестность вблизи этой точки и есть переходное состояние – область конфигурацииQ, в которой с большей вероятностью происходит перестройка электронного состояния.
Введем классическое время пребывания
системы в переходном состоянии:
![]() ,
гдеv– скорость
движения ядер. Введем времяif- среднее время перестройки электронного
состояния изiвf. Возможны два предельных случая:
,
гдеv– скорость
движения ядер. Введем времяif- среднее время перестройки электронного
состояния изiвf. Возможны два предельных случая:
1)
![]() 2)
2)
![]()
Р

![]() ,
где квадраты коэффициентов – вероятность
найти электроны в состоянииiиf.
По теории возмущений в вырожденном
случае получаем, что в системе будут
существовать два состояния
,
где квадраты коэффициентов – вероятность
найти электроны в состоянииiиf.
По теории возмущений в вырожденном
случае получаем, что в системе будут
существовать два состояния![]() и
и![]() с энергией:
с энергией:![]() и
и![]() .
.
Вероятность электронного обмена
максимальна в точке пересечения термов
и резко падает по мере удаления от нее
при возрастании
![]() .
Можно сконструировать электронные
термы, соответствующие состояниям
.
Можно сконструировать электронные
термы, соответствующие состояниям![]() и
и![]() .
В точке пересечения термов:
.
В точке пересечения термов:
![]() и
и![]() .
.
При отклонении от Q* термыU+иU-гладко переходят в термы начального и
конечного состояний. ТермыU+иU-называют
адиабатическими, термы![]() и
и![]() –
диабатическими.
–
диабатическими.
Таким образом, при
![]() переход
из начального в конечное состояние
трактуется как плавный переход с терма
переход
из начального в конечное состояние
трактуется как плавный переход с терма![]() на термU+и далее
на
на термU+и далее
на![]() .
.
(2)
![]() .
Вероятность того, что система успеет
перестроиться в переходном состоянии,
мала и пропорциональна
.
Вероятность того, что система успеет
перестроиться в переходном состоянии,
мала и пропорциональна
![]() .
Такие процессы называются неадиабатическими.
В этом случае система движется по
диабатическому терму
.
Такие процессы называются неадиабатическими.
В этом случае система движется по
диабатическому терму![]() и
с малой вероятностью переходит на
диабатический терм
и
с малой вероятностью переходит на
диабатический терм![]() .
.
Критерий адиабатичности
Оценим
![]() из
соотношения неопределенности:
из
соотношения неопределенности:![]() (аналогично
(аналогично![]() )
)
В переходной области должен выполняться
принцип Франка-Кондона, т.е.
![]() .
Так как размер переходной области
невелик, то можно заменить
.
Так как размер переходной области
невелик, то можно заменить![]() на
производную
на
производную .
Обозначим ее через
.
Обозначим ее через![]() .
Следовательно,
.
Следовательно,![]() ,
откуда
,
откуда![]() .
Положим
.
Положим![]() ,
гдеv –
скорость прохождения переходной области
при классическом надбарьерном протекании
реакции:
,
гдеv –
скорость прохождения переходной области
при классическом надбарьерном протекании
реакции:
![]() .
Таким образом, если
.
Таким образом, если
![]() ,
то
,
то![]() (неадиабатическая реакция) и наоборот,
если
(неадиабатическая реакция) и наоборот,
если
![]() ,
то
,
то![]() (адиабатическая реакция).
(адиабатическая реакция).
Строгий квантовохимический расчет дает для вероятности перехода Р следующее выражение:
![]()
где
![]() -
фактор неадиабатичности (Ландау-Зинера).
-
фактор неадиабатичности (Ландау-Зинера).
Р 1, при>> 1 – адиабатическая реакция. Р2, при<< 1 – неадиабатическая реакция.
Причины нарушения адиабатичности:
Мало обменное взаимодействие:
 0 (мала область переходного состояния)
0 (мала область переходного состояния)Велика скорость движения ядер (система быстро проскакивает переходную область)
Примечание: Вид поверхности потенциальной
энергии, а следовательно и величина![]() неизвестны,
неизвестны,![]() тоже
можно только оценивать, соответственно
невозможно точно рассчитать параметр и решение
вопроса об адиабатичности реакции часто
проводится на основе сопоставления
теоретической и экспериментальной
константы скорости, что не является
однозначным и доказательным фактом.
тоже
можно только оценивать, соответственно
невозможно точно рассчитать параметр и решение
вопроса об адиабатичности реакции часто
проводится на основе сопоставления
теоретической и экспериментальной
константы скорости, что не является
однозначным и доказательным фактом.
