
- •Лекции по курсу «Кинетика жидкофазных реакций»
- •Раздел I. Введение в кинетику жидкофазных реакций. Структура жидкости
- •Тема 1. Диффузионный и кинетический контроль в кинетике жидкофазных реакций
- •Вязкость. Уравнение Стокса – Эйнштейна. Численная оценка kD.
- •Оценка частоты столкновений в жидкости
- •Тема 2. Представление о структуре жидкости
- •Движение в квазикристаллической среде
- •Раздел II. Межмолекулярные взаимодействия и сольватация
- •Тема 3. Парные электростатические взаимодействия
- •Напряженность поля диполя (f):
- •Энергия взаимодействия зарядов
- •Энергия взаимодействия системы зарядов во внешнем поле
- •Индукционное взаимодействие
- •Дисперсионное взаимодействие
- •Донорно-акцепторные (д-а) комплексы и водородная связь
- •Тема 4. Континуальные модели взаимодействия растворенной молекулы с растворителем Сольватация ионов
- •Уравнение Борна-Бьеррума (4.2)
- •Теория Дебая – Хюккеля
- •Раздел 3. Диффузионно – контролируемые реакции (дкр)
- •Тема 5. Дкр в рамках теории Смолуховского
- •Граничное условие 3-рода
- •Уравнение Смолуховского для вероятностей
- •Тема 6. Учет взаимодействия реагентов в уравнении Смолуховского
- •Тема 7. Геминальная рекомбинация
- •Тема 8. Учет анизотропии реагентов
- •Тема 9. Дкр с дальнодействием
- •Вывод уравнения Штерн – Фольмера
- •Перенос энергии в жидких растворах
- •Раздел IV. Кинетически-контролируемые реакции
- •Тема 10. Кинетически-контролируемые реакции в рамках теории активированного комплекса (так)
- •Характерные времена релаксационных процессов в растворителях
- •Раздел V. Влияние давления на скорость химических реакций
- •Кинетически контролируемые реакции
- •Раздел VI. Элементы квантовой теории химических реакций. Перенос электрона
- •Тема 12. Элементы квантовой теории химических реакций
- •Туннельные реакции
- •Усреднение вероятности реакции по ансамблю
Тема 8. Учет анизотропии реагентов
Рассмотрим следующую модель: реакция изотропной частицы А с частицей В, на поверхности которой есть реакционный участок с телесным углом 0- «белая сфера с черным пятном». Задача эквивалентна задаче о диффузии точечной частицы А к сфере радиусомRA+RBи реакционным пятном на поверхности. Посчитаем площадь реакционной зоны:
 (8.1)
(8.1)
Объем реакционной зоны:
![]() ,
где- толщина
реакционного слоя, аf– геометрический фактор. Далее, обозначим
количество эффективных столкновений
какZeffи, предполагая, что отношение времени
пребывания в зоне реакции ()
к времени свободного движения (1/Zeff)
равно отношению реакционного объемаVrк свободному объемуVf
= 1/C. Тогда:
,
где- толщина
реакционного слоя, аf– геометрический фактор. Далее, обозначим
количество эффективных столкновений
какZeffи, предполагая, что отношение времени
пребывания в зоне реакции ()
к времени свободного движения (1/Zeff)
равно отношению реакционного объемаVrк свободному объемуVf
= 1/C. Тогда:![]() .
Величина –Zeff/Спо определению константа диффузионных
встреч (kD).
Таким образом,kD= Vr/.
.
Величина –Zeff/Спо определению константа диффузионных
встреч (kD).
Таким образом,kD= Vr/.
Для изотропных реагентов из решения уравнения Смолуховского было найдено, что среднее время пребывания частицы в реакционном слое = R/D. Используя этот факт, получим, что kD = Vr/ = 4RD – правильное решение для изотропной задачи.
В случае анизотропии реагентов kD= 4R2f/
и задача сводится к нахождению времени. Оказалось, что
время зависит от геометрического
стерического фактора как![]() ,
следовательноkD= 4DReff
(8.2), где
,
следовательноkD= 4DReff
(8.2), где![]() .
Т.е. все дело в перенормировке контактного
радиуса иkD
.
Т.е. все дело в перенормировке контактного
радиуса иkD
![]() .
.
Тема 9. Дкр с дальнодействием
Процессы переноса энергии и электрона. В этом случае реакция вводится не как граничное условие, а входит в виде дополнительного члена в диффузионное уравнение.
Начнем с рассмотрения процесса передачи энергиимежду донором (D) и акцептором (А):
![]()
Если оба электронных перехода А А* иDD* разрешены в дипольном
приближении, то взаимодействием,
приводящим к переносу энергии является
диполь-дипольное взаимодействие.V
1/r3.
Вероятность передачи энергии по теории
возмущений пропорциональна![]() .
Тогдаk(r)
.
Тогдаk(r)
![]() =a/r6.
Если оба перехода или один из них запрещен
в дипольном, но разрешен в квадрупольном
приближении, тоk(r)
a/r8
(диполь-квадруполь) иk(r)
a/r10
(квадруполь-квадруполь).
=a/r6.
Если оба перехода или один из них запрещен
в дипольном, но разрешен в квадрупольном
приближении, тоk(r)
a/r8
(диполь-квадруполь) иk(r)
a/r10
(квадруполь-квадруполь).
Если один из переходов запрещен по
спину, то имеем обменное тушение
![]()
Где k0– константа скорости реакции на контакте,L- характерный параметр затухания волновых функций. Следует отметить, что в ходе всего процесса должен сохраняться полный спин системы.
Для начала рассмотрим задачу о затухании
люминесценции в присутствии тушителя
в жестких средах (матрицы) – в условиях,
когда диффузией реагентов можно
пренебречь. Пусть
![]() - плотность частиц донора энергииDна расстоянииR1,
R2
… RNот которых находитсяNакцепторовА. Тогда, для зависимостиот времени
можно записать:
- плотность частиц донора энергииDна расстоянииR1,
R2
… RNот которых находитсяNакцепторовА. Тогда, для зависимостиот времени
можно записать:
 ,
где0– собственное время жизни донора.
,
где0– собственное время жизни донора.
Решение имеет вид![]() .
Предположим, что все молекулы по раствору
распределены статистически равновероятно
и усредним
.
Предположим, что все молекулы по раствору
распределены статистически равновероятно
и усредним![]() :
:

При выводе последней формулы мы совершили
предельный переход N
,V
,
CA
= N/V
= const. Тогда![]()
Если у нас тушение по диполь-дипольному
механизму, то
![]() ,
гдеR0–
Ферстеровский радиус (расстояние на
котором константа тушения равна 1/0).
Если пренебречь собственными объемами
донора и акцептора можно вычислить:
,
гдеR0–
Ферстеровский радиус (расстояние на
котором константа тушения равна 1/0).
Если пренебречь собственными объемами
донора и акцептора можно вычислить:
 (9.1)
(9.1)
Видно, что кинетика существенно неэкспоненциальна и собственно говоря, ввести понятие константы скорости нельзя.
Вывод уравнения (9.1)
 ,
где
,
где
![]() .
Вспомним, что
.
Вспомним, что![]() и найдем
и найдем :
Тогда нетрудно видеть, что
:
Тогда нетрудно видеть, что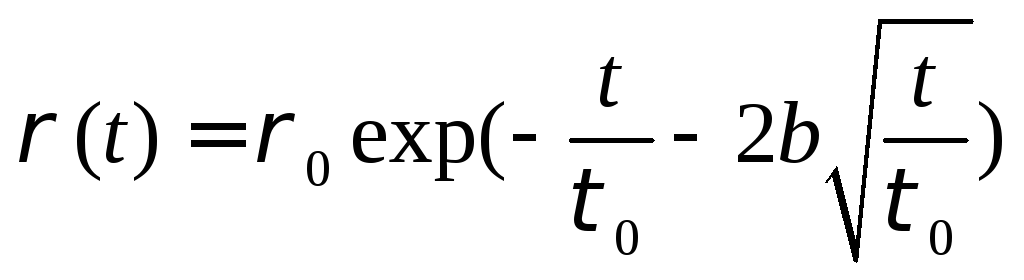 .
Это можно проверить дифференцированием.
.
Это можно проверить дифференцированием.
Случай обменного тушения ![]() .
Результат в общем случае может быть
получен только численным интегрированием.
Рассмотрим предельные случаи:
.
Результат в общем случае может быть
получен только численным интегрированием.
Рассмотрим предельные случаи:
(1) малые времена: k0t
<< 1 ![]() (9.2)
(9.2)
(2) большие времена:k0t
>> 1 ![]()
Т.е. на малых временах кинетика носит
экспоненциальный характер и можно
ввести эффективную константу скорости
тушения
![]() Т.е. фактически мы рассматриваем реакцию
в тонком слое толщинойL/2.
В случае обменного тушении понятие
толщина реакционного слоя имеет ясный
физический смысл – это характерный
спад константы тушения вераз.
Т.е. фактически мы рассматриваем реакцию
в тонком слое толщинойL/2.
В случае обменного тушении понятие
толщина реакционного слоя имеет ясный
физический смысл – это характерный
спад константы тушения вераз.
Вывод формулы (9.2)
![]() ;
;
![]()

