3.6. Основні поняття теорії кінцевих автоматів

Кінцевим автоматом називається система S={A, Q, V, }, у котрої A={a₁,…,a_m},Q={q₁,…q_n},V={v₁,…,v_k}- кінцеві множини (алфавіти); a : Q x A  Q і : Q x A  V - функції, визначені на цих множинах. А називається вхідним алфавітом, V - вихідним алфавітом, Q - алфавітом стана;  - функцією переходів,  - функцією виходів. Якщо, крім того, в автоматі S виділене один стан, який називається початковим (будемо вважати, що цей стан q₀), то отриманий автомат називається ініціальним і позначається ( S, q₀ ) ; таким чином, по не ініціальному автоматі з n станами можна n різноманітними засобами визначити ініціальний автомат.

Оскільки функції  і визначені на кінцевих множинах, їх можна задавати таблицями. Звичайно дві таблиці зводяться в одну таблицю  і , яка називається таблицею переходів - виходів автомата або автоматною таблицею.

Приклад. Таблиця 3.5 задає функції переходів і виходів для автомата з алфавітами A = { a₁, a₂, a₃}, Q = {q₁, q₂, q₃, q₄}, V = {v₁, v₂}.

Таблиця 3.5 - Табличне завдання кінцевого автомата

	a1	a2	a3
q1	q3 / v1	q3 / v2	q2 / v1
q2	q4 / v1	q1 / v1	q1 / v1
q3	q2 / v1	q3 / v1	q3 / v2
q4	q4 / v1	q2 / v1	q1 / v2

Ще один поширений і наочний засіб завдання автоматів - орієнтований мультиграф, називаний графом переходів або діаграмою переходів. Вершини графа відповідають станам; якщо  (q_i, a_j) = q_k і (q_i, a_j)= v_l, то з q_i у q_k веде ребро, на якому написані a_j і v_l . Граф переходів для таблиці 3.5 зображений на рис. 3.7. Кратні ребра не обов'язкові; наприклад два ребра з q₂ у q₁ можна замінити одним, на якому будуть написані обидві пари a₃/v₁ і a₂/v₁ . Для будь-якого графа переходів у кожній вершині q_i виконані такі умови, що називаються умовами коректності:

1) Для будь-якої вхідної букви ai є ребро, що виходить із qi, на якому написане aj (умова повноти);

2) Будь-яка буква aj зустрічається тільки на однім ребрі, що виходить із qi (умова несуперечності або детермінованості).

Для даного автомата S його функції _S і _S можуть бути визначені не тільки на множині А усіх вихідних буквах, але і на множині А* усіх вхідних слів. Для будь-якого вхідного слова _j _j2_jkq_i, a_j1, a_j2, … , a_jk q_i, a_j1), a_j2), … ,

a_jk-₁), a_jk).

a₁/v₁

a₁/v₁

a₂/v₁

a₁/v₁

a₂/v₁

a₃/v₁

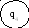
a₃/v₂

a₂/v₂

a₁/v₁

a₁/v₁

a₂/v₁

a₃/v₂

Рис. 3.7 - Граф кінцевого автомата

Іншим способом це традиційне визначення можна представити таким чином:

1)  ( Qi , aj ) задається автоматною таблицею s;

2) Для будь-якого слова а* і будь-якої букви аj

q_i,a_jq_i,a_j).

Тут і надалі символи станів для формування коротких позначень будуть замінятися їхніми індексами.

За допомогою розширеної функції  визначається (індуктивно) розширена функція .

q_ia_jq_ja_j).

Зафіксуємо в автоматі S початковий стан q₁ і кожному вхідному слову  = а_j1, а_j2, …, а_jk поставимо у відповідність слово  у вихідному алфавіті:

q₁, a_j1q₁,a_j1a_j2q₁,a_j1,…,a_jk.

Ця відповідність, що відображає вхідні слова у вихідні слова називається автоматним відображенням, а також автоматним оператором. Якщо результатом застосування оператора до слова  є вихідне слово , те це будемо позначати відповідно S (q₁, ) =  або S( ) = . Число букв у слові , як звичайно є довжиною  і позначається або l(

Автоматне відображення має такі властивості:

• слова  і  = S( ) мають однакову довжину;

• якщо  = __ і S(__)= __ , де _= _ , то S( _ )= _.

Остання властивість відбиває той факт, що автоматні оператори - це оператори, які, переробляючи слово зліва праворуч, не «заглядають вперед». При цьому i - я буква вихідного слова залежить тільки від перших i - букв вихідного слова.

Зазначені властивості були б достатніми умовами автоматного відображення, якби мова йшла про нескінечені автомати. Для кінцевих автоматів цих умов недостатньо при реалізації для довільних вхідних і вихідних алфавітів.