
Дом задание_1.1 Множества
.pdf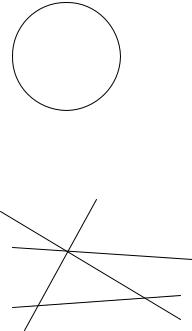
Множества. Способы задания множеств
1.Приведите примеры множеств. Задайте их различными способами.
2.М – множество точек окружности, изображенной
на рисунке 1. Прочитайте следующие предложения и укажите среди них верные:
а) в)
АМ
ВМ
;
;
б) г)
ОМ
СМ
;
.
Рис. 1
3. Как изменить условие задачи 2, чтобы все утверждения были верными?
4. Запишите с помощью знаков и , какие из отрезков АВ, СD, EF, PH проходят через точку М, а какие через нее не проходят. (Рисунок 2)
Рис. 2
5.Запишите множество букв в слове «математика», «юриспруденция» и множество цифр в записи числа 5125353.
6.Запишите с помощью перечисления предложения:
а) Х – множество чисел 0, 1, 2, 3, 4, 5; б) У – множество букв a, b, c.
7.Используя символы, запишите множество Р, если оно состоит из натуральных чисел:
а) больших 100, но меньше их 200; б) меньших 150.
8.Укажите характеристическое свойство элементов множества:
а) б) в)
а, е, ё,и, о, у, э, ю, я,ы ;
78,76,74,72,70 ;
111,222,333,444,555,666,777,888,999 .
9. Множество двузначных чисел, оканчивающихся 1. Принадлежат ли этому множеству числа 31, 321, 21, 61, 12. Ответ запишите, используя знаки и.
Отношения между множествами
1. Даны два множества
X
2,4,6
и Y 0,2,4,6,8 . Верно ли, что:
а) множества X и Y пересекаются? Запишите новое множество; б) множество X является подмножеством множества Y ;
в) множество P 4,0,6,8,2 равно множеству Y ?
2. Изобразите при помощи кругов Эйлера отношения между множествами |
С |
|
и D |
, если: |
|
а) С |
- множество двузначных чисел, |
|
D
3,43,34,56,103
;
б) С D в) С D г) С D 3. Дано
-множество двузначных чисел,
-множество четных натуральных чисел;
-множество двузначных чисел,
-множество трехзначных чисел;
-множество двузначных чисел,
-множество натуральных чисел, не меньших 10.
множество |
P 3,5,7,9 . Образуйте всевозможные его подмножества. |
Сколько их должно быть?
Пересечение множеств
1. Сформулируйте условия, при которых истинны следующие утверждения:
|
а) |
5 A B ; б) 7 A B . |
|
|
2. |
Известно, что x A . Следует ли из этого, что |
x |
||
|
Эйлера-Венна. |
|
|
|
3. |
Известно, что x A B . Следует ли из этого, что |
|||
|
Эйлера-Венна. |
|
|
|
4. |
Найдите пересечение множеств A и B , если: |
|
||
|
а) |
A a,b, c, d, e, f , B b,t, f , k ; |
|
|
|
б) |
A 26,39,5,58,17,81 , |
B 17,26,58 ; |
|
|
в) |
A 26,39,5,58,17,81 , |
B 17,26,58,5,39,81 . |
|
B A
?Поясните на кругах
?Поясните на кругах
5. Из каких элементов состоит пересечение множества букв в слове «математика» и множества букв в слове «информатика»; пересечение множества букв в слове «математика» и множества букв в слове «юриспруденция»?
Объединение множеств
1. Сформулируйте условия, при которых истинны следующие утверждения:
а)
5
A
B
; б) 7 A B .
2.Известно, что x A . Следует ли из этого, что x A B ? Поясните на кругах Эйлера-Венна.
3.Известно, что x A B . Следует ли из этого, что x A ? Поясните на кругах Эйлера-Венна.
4.Найдите объединение множеств A и B , если:
а) A a,b, c, d, e, f , B b,t, f , k ;
б) A 26,39,5,58,17,81 , B 17,26,58 ;
в) A 26,39,5,58,17,81 , B 17,26,58,5,39,81 .

5. Из каких элементов состоит объединение множества букв в слове «математика» и множества букв в слове «информатика»; пересечение множества букв в слове «математика» и множества букв в слове «юриспруденция»?
Свойства пересечения и объединения множеств
1. |
Известно, что |
x A B . Следует ли из этого, что: |
||
|
а) x B A ; |
б) |
x A B ; |
в) x B A ? |
2. |
Определите порядок выполнения действий в следующих выражениях: |
|||
|
а) A B C ; |
|
б) A B C D ; |
|
|
в) A B C ; |
|
г) A B C D . |
|
3. |
Постройте три круга, представляющие попарно пересекающиеся |
|||
|
множества А, В и С, и отметьте штриховкой области, изображающие |
|||
|
множества: |
|
A B C ; |
|
|
а) A B C ; |
в) |
д) A B C ; |
|
|
б) A B C ; |
г) |
A B C ; |
е) A C B C . |
Для каждого случая сделайте отдельный рисунок.
4. Верно ли, что если |
A B , то: а) |
A B A; |
б) |
A B B ? |
Вычитание множеств. Дополнение множества
1. |
Известно, что x A \ B . Следует ли из этого, |
||
2. |
Найдите разность множеств А и В, если: |
||
|
а) |
A 1,2,3,4,5,6 , |
B 2,4,6,8,10 ; |
|
б) |
A 1,2,3,4,5,6 , |
B ; |
|
в) |
A 1,2,3,4,5,6 , |
B 1,3,5 ; |
|
г) |
A 1,2,3,4,5,6 , |
B 6,2,3,4,5,1 . |
что: а)
x
A
;
б)
x
B
?
3.В каких случаях, выполняя упражнение 2, вы находили дополнение множества В до множества А?
4.Постройте три круга, изображающие три попарно пересекающихся множества А, В и С, и выделите каким-либо образом области, представляющие множества:
а) б)
A B \
A \ B
C ; C ;
в) г)
A \ C B \ C A \ B C ;
;
д) е)
A \ (B C)
(A \ B) C
;
.
Для каждого случая выполните отдельный рисунок.
