18_konspekt

Лекция 18 Площадь многоугольника. Объем многогранника.

Литература [1] § 86 ‑ 90, [2] § 26 ‑ 28.

Определение 23.1. Многоугольником называется множество точек плоскости, являющееся объединением конечного числа, попарно не имеющих общих внутренних точек треугольников.

Таким образом, многоугольник М равен объединению треугольников Тi: , где треугольники T_i и T_j не имеют общих внутренних точек при всех i, j=1, ...,n. Будем говорить в этом случае, что многоугольник M составлен из треугольников (или разложен на треугольники) T_i, i=1, ...,n, и записывать M=T₁+T₂+...+T_n или коротко: . Внутренние точки треугольников Т_i будем называть внутренними точками многоугольника М. Аналогичных соглашений и записи будем придерживаться и в том случае, когда многоугольник M является объединением конечного числа, попарно не имеющих общих внутренних точек (или составлен из) многоугольников M_i, i=1, ...,n. В этом случае также будем использовать запись . Множество всех многоугольников плоскости будем обозначать через . Ясно, что все многоугольники, изучаемые в школьном курсе геометрии, удовлетворяют определению 23.1.

Определение 23.2. Пусть дано отображение s множества  многоугольников плоскости на множество действительных чисел R. s: R, удовлетворяющее следующим условиям (аксиомам площади):

1. (Аксиома позитивности) Для любого многоугольника M имеет место неравенство s(M)0.

2. (Аксиома инвариантности) Любые два конгруэнтных¹ многоугольника MN имеют равные площади: s(M)=s(N).

3. (Аксиома аддитивности) Если многоугольник M составлен из двух² многоугольников M₁ и M₂, M=M₁+M₂, то s(M)=s(M₁)+s(M₂).

4. (Аксиома нормированности) Площадь единичного квадрата³ Q равна единице: s(Q)=1.

Тогда число будем называть площадью многоугольника.

Л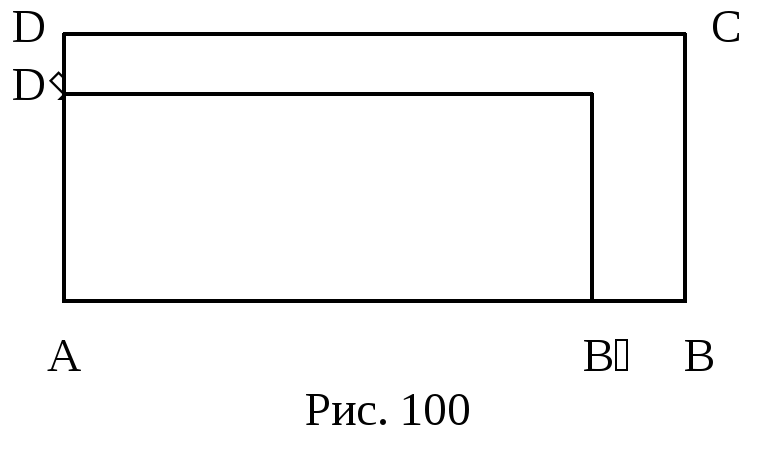емма 23.1. Пусть прямоугольник P₁=ABCD содержится в прямоугольнике P₂=ABCD, причем точка B лежит на стороне AB, а точка D - на стороне AD. Тогда s(P₁)s(P₂).

Доказательство. В силу аксиомы 3 площади (см. определение 23.2) имеет место равенство s(P₁)+s(M)=s(P₂), где через M обозначен шестиугольник BCDDCB (рис. 100), который, как нетрудно видеть, является многоугольником в смысле определения 23.1. Но из аксиомы 1 площади следует, что s(M)0. Поэтому s (P₁)s(P₂). Лемма доказаниа.

Лемма 12.2. Пусть P произвольный прямоугольника со сторонами a и b. Тогда s(P)=ab.

Д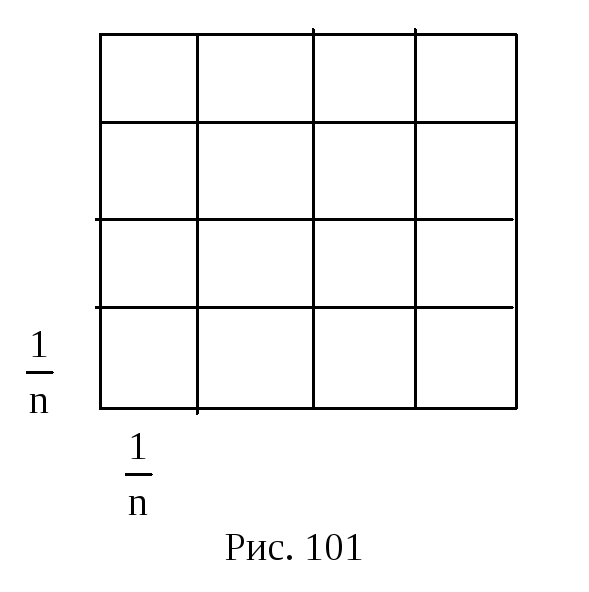оказательство. Рассмотрим следующие три случая. Предположим, во-первых, что прямоугольник Р, таким образом, представляет собой квадрат со стороной, равной , , где n - некоторое натуральное число. Разложим единичный квадрат Q на n² квадратов со стороной 1/n (рис.101) . Положим s(P)=c. В силу аксиомы 2 определения 23.2 s(P_i)=c при любом i=1,...n², поскольку все квадраты со стороной конгруэнтны между собой. Из аксиомы 3 этого же определения следует, что , откуда , следовательно, s(P)=c==ab, что доказывает справедливость утверждения леммы в рассматриваемом случае.

Второй случай произвольных рациональных значений и с помощью аксиомы 3 определения 23.2 по индукции сводится к только что рассмотренному случаю. Действительно, положив n=n₁n₂, получим и . Поэтому данный прямоугольник P можно составить из m₁n₂m₂n₁ квадратов со стороной и, следовательно, в силу аксиомы 3 справедливо равенство , из которого следует истинность утверждения леммы в рассматриваемом случае.

В третьем случае стороны прямоугольника Р a и b представляют собой произвольные действительные числа. Воспользуемся леммой 23.1 и с помощью предельного перехода сведем его к случаю рациональных значений a и b. Возьмем произвольные рациональные приближения действительных чисел a и b с недостатком и избытком: , где рациональные числа a_n, b_n, a_n, b_n удовлетворяют неравенствам a_na, b_nb, и a_na, b’_n b при всех натуральных n.

Нетрудно видеть, что прямоугольник P_n со сторонами a_n и b_n можно вложить в прямоугольник P так, как показано на рисунке 100. В силу леммы 23.1 из этого следует, что a_nb_n=s (P_n)s (P) при всех n. Аналогично, s (P)s(P_n)=a_nb_n, при всех n, где через P_n обозначен прямоугольник с рациональными сторонами a_n и b_n. Таким образом, неравенство a_nb_ns(P)a_nb_n справедливо при всех n. Переходя в последнем неравенстве к пределу, получаем: , поэтому s (P)=ab. Лемма доказана.

Лемма 23.3. Для произвольного треугольника T со сторонами a, b, c; углами A, B, C - и соответствующими высотами имеют место равенства:

.

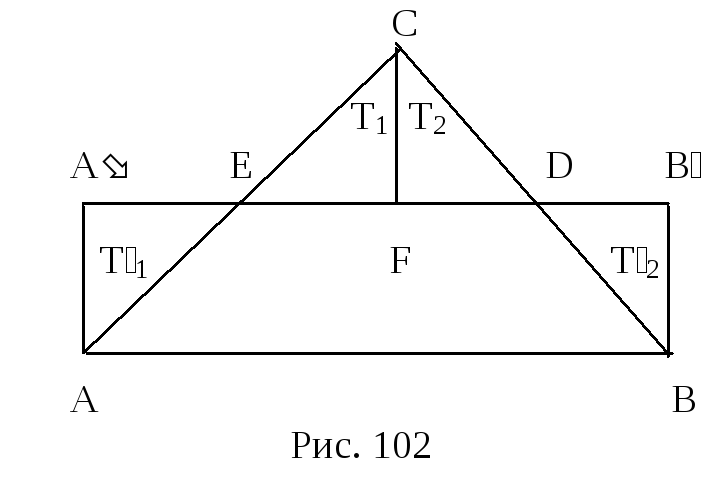Доказательство. Пусть T - данный треугольник с вершинами в точках A, B и C, причем AB=c - его большая сторона. На стороне AB построим прямоугольник P=ABBA со сторонами AB=c и AA=. Проведем отрезок CF, перпендикулярный AB. Обозначим через E и D середины сторон АС и АВ, а через Т₁, Т₂, Т₁ и Т₂ соответственно треугольники CFE, CFD, AAE и BB D (рис. 102). Так как АВ большая сторона данного треугольника, легко установить, что F – внутренняя точка отрезка ED (докажите этот факт самостоятельно).Имеют место следующие разложения: P=ABDE+T₁+T₂ и T=ABDE+T₁+T₂. Следовательно, в силу аксиомы 3 площади многоугольника

s(P)=s (ABDE)+s (T₁)+s (T₂), s(T)=s(ABDE)+s(T₁)+s(T₂). (23.1)

Вместе с тем, нетрудно доказать конгруэнтность треугольников T₁T₁ и T₂T₂, что в силу аксиомы 2 площади, влечет справедливость равенств s(T₁)=s(T₁) и s(T₂)=s(T₂). Отсюда и из равенств (23.1), в силу леммы 23.2, получим:

s(T)=s(ABDE)+s(T₁)+s(T₂)=s(ABDE)+s(T₁)+s(T)=s(P)=ABВA= ,

что доказывает справедливость одного из требуемых условием леммы равенств. Поскольку h_c=bsinA, то , что доказывает справедливость еще одного из приведенных в условии леммы соотношений. Остальные равенства выводятся с помощью теоремы синусов из доказанных равенств, что и предлагается читателю в качестве упражнения. Лемма доказана.

Теорема 23.4 (о единственности площади многоугольника). Существует не более одного отображения s: R, удовлетворяющего аксиомам площади 1-4.

Доказательство. Непосредственно следует из леммы 23.3 и аксиом площади. Пусть отображения s: R, и s: R, удовлетворяют аксиомам площади 1-4 и M - произвольный многоугольник, покажем, что s(M)=s (M). Из определения 23.1 следует, что найдутся треугольники T₁, T₂,...,T_n, для которых имеет место разложение M=T₁+T₂+...+T_n. В силу леммы 23.3 равенства s(T_i)=s(T_i) справедливы при всех i=1, ..., n. А в силу аксиомы 2 площади имеем: s(M)=s(T₁)+...+ s(T_n)=s(T₁)+...+ s(T_n)=s(M). Теорема доказана.

Обсудим, как установить существование отображения s: R, удовлетворяющего определению 23.2. Из леммы 23.3 следует, что площадь треугольника должна удовлетворять известным формулам. Поэтому введем следующее определение.

Определение 23.3. Определим на множестве  всех треугольников плоскости  отображение s:R, положив для произвольного треугольника T со сторонами «a» и «b» и углом «» между ними ⁴.

Теперь для вычисления площади произвольного многоугольника можно использовать его разложение на треугольники. Однако на этом пути встает непростой вопрос. Один и тот же многоугольник, в частности треугольник, допускает различные разложения на треугольники: и , где M_i и N_j - некоторые треугольники. Поэтому для корректности такого определения нужно, чтобы равенство

(23.2)

имело место для любых двух разложений многоугольника M на треугольники.

Под ориентированным треугольником будем понимать произвольную упорядоченную тройку точек (АВС) плоскости. Если точки лежат на одной прямой, то ориентированный треугольник (АВС) будем называть вырожденным. Зафиксируем в евклидовом пространстве некоторую прямоугольную декартовую систему координат O так, чтобы точка O лежала в плоскости , а векторы и были ей параллельны.

Определение 23.4. Под площадью ориентированного треугольника (ABC) будем понимать число , где - смешанное произведение векторов и .

Из свойств смешанного произведения векторов (см. [1]) следует, что для вырожденного треугольника. Если треугольник не вырожден, то знак числа s₀ зависит от ориентации базиса . Если этот базис правый, т.е. его ориентация совпадает с ориентацией базиса , то , если левый, то .

Лемма 23.5. Для трех произвольных точек A, B, C справедливы равенства: .

Доказательство. Воспользуемся свойствами смешанного произведения векторов (см. [1]). Докажем, например равенство s₀(ABC)=s₀(BCA) Из определения значения s₀(ABC) следует, что:

Доказательства остальных равенств проводится аналогично. Лемма доказана.

Поскольку из доказанной леммы следует, что ориентированные треугольники (ABC), (BCA) и (CAB) имеют равные площади, то мы будем их считать одним и тем же ориентированным треугольником так же, как и тройку ориентированных треугольников (BAC), (ACB), (CBA). Таким образом, каждому неориентированному треугольнику ABC соответствуют два ориентированных треугольника: ABC и ACB, площади которых противоположны.

Н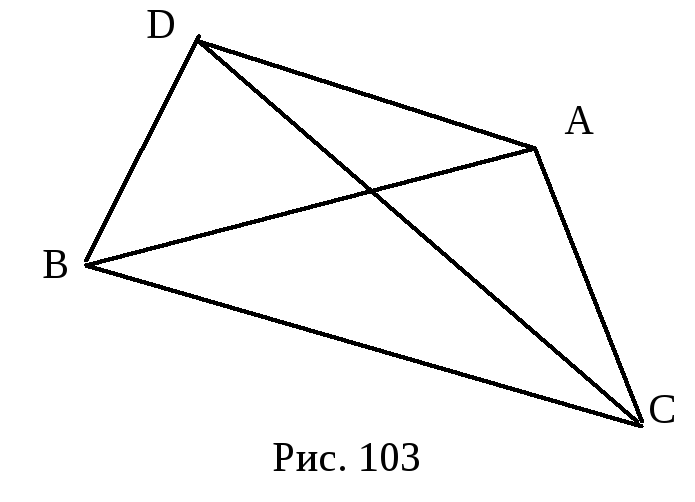етрудно видеть, модуль площади ориентированного треугольника равен площади соответствующего ему неориентированного треугольника. Действительно, как следует из свойств смешанного произведения векторов (см. [1]), совпадает с объемом параллелепипеда, построенного на векторах , и . Вектор перпендикулярен плоскости , т.е. векторам и , и его длина равна 1. Поэтому объем этого параллелепипеда равен модулю векторного произведения векторов и , т.е. произведению модулей сомножителей на синус угла между ними. Отсюда и из определений 23.3 и 23.4 следует, что .

Лемма 23.6. Для произвольного ориентированного треугольника ABC и произвольной точки D справедливо равенство:

.

Доказательство. Пусть (АВС) – данный ориентированный треугольник, D - произвольная точка плоскости (рис. 103). Из определения 23.4, свойств смешанного произведения векторов и леммы 23.5 получим:

В частности, из доказанной леммы несложно вытекает следующее следствие.

Следствие. Для произвольного треугольника ABC и точки D, лежащей на стороне AB, справедливы равенства:

, (23.3)

(23.4)

Доказательство. В силу леммы 23.6 имеет место равенство , но , поскольку точки D, A, B - коллинеарны, откуда и следует равенство (23.3).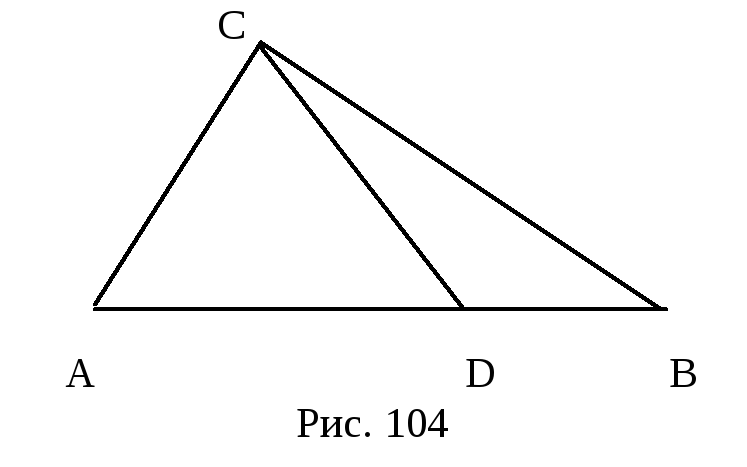

Равенство (23.4) непосредственно следует из леммы 23.3, поскольку треугольники DBC и DCA имеют общую высоту, проведенную из вершины C, а сумма их оснований AD и DB равна основанию AB треугольника ABC.

Равенство (23.4) позволяет свести случай произвольных разложений многоугольника на треугольники к “правильным” их разложениям, называемым триангуляциями.

О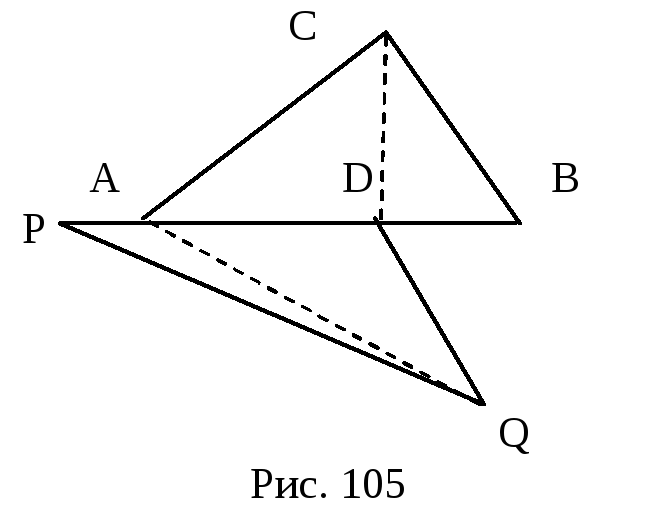пределение 23.5. Разложение многоугольника M на треугольники называется триангуляцией, в случае если пересечение любых двух треугольников при ij, является: либо пустым множеством, либо их общей вершиной, либо их общей стороной.

Лемма 23.7. Для любого разложения многоугольника M на треугольники существует триангуляция многоугольника M такая, что

.

Доказательство. Пусть M=T₁+T₂+...+T_n - произвольное разложение многоугольника M на треугольники. Предположим, что вершина D некоторого треугольника PQD этого разложения лежит внутри стороны AB треугольника ABC, который также является элементом данного разложения (рис.105). Соединим точку D с противоположной вершиной C треугольника ABC (пунктирная линия на рисунке). Заменив в имеющемся разложении многоугольника M треугольник ABC двумя треугольниками ADC и DBC, получим новое разложение M на треугольники, сумма площадей которых равна сумме площадей исходного разложения, так как из равенства (23.4) следует: s(ABC)=s(DBC)+s(ADC). Проделав последовательно описанное выше действие со всеми треугольниками, содержащими внутри некоторой своей стороны вершину какого-либо другого треугольника, получим, триангуляцию {T₁, T₂, ..., T_m}, удовлетворяющую условию леммы

Следующее утверждение устанавливает аддитивность определенного выше на множестве треугольников отображения s:R.

Лемма 23.8. Для любого разложения треугольника T на треугольники имеет место равенство .

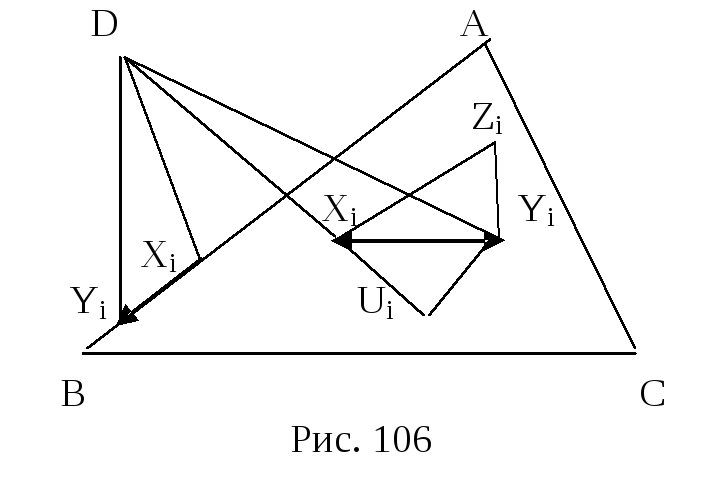Доказательство. Пусть T=T₁+T₂+...+T_n произвольные разложения данного треугольника T. В силу леммы 23.7 найдется триангуляция {T₁,..., T_m} треугольника T, для которой имеет место равенство

s(T₁)+s(T₂)+...+s(T_n)=s(T₁)+s(T₂)+...+s(T_m).

Покажем, что s(T)=s(T₁)+s(T₂)+...+s(T_m), откуда и будет следовать справедливость утверждения леммы.

Выберем положительную ориентацию треугольников T, T₁, T₂, ..., T_m (рис.106). Для наглядности будем считать, что вершины положительно ориентированных треугольников обходятся против часовой стрелки. Возьмем произвольную точку D и представим площадь каждого из ориентированных треугольников T_i, i=1,..., m в виде суммы площадей трех ориентируемых треугольников, одна из вершин которых совпадает с точкой D (см. рис. 106) s₀(T_i)=s₀(DX_iY_i)+s₀(DY_iZ_i)+s₀(DZ_iX_i), где T_i=X _iY_iZ_i. Суммируя последнее равенство по всем i=1,..., m, получим

s₀(T₁)+ s₀(T₂)+...+ s₀(T_m)=, (23.5)

где суммирование в правой части идет по всем сторонам всех положительно ориентированных треугольников T, T₁, T₂, ..., T_m. Покажем, что правая часть равенства (23.5) совпадает с s₀(T).

Рассмотрим два случая: когда сторона X_iY_i лежит внутри треугольника T, и когда сторона X_iY_i лежит на одной из сторон треугольника T. В первом случае, найдутся ровно два треугольника триангуляции со стороной X_iY_i. Обозначим их через Z_iX_iY_i и U_iX_iY_i. В разложение первого из этих треугольников, согласно лемме 23.6, входит слагаемое DX_iY_i, а в разложение второго - слагаемое DY_iX_i (см. рис. 106) В силу леммы 23.5 имеет место равенство s₀(DX_iY_i)+s₀(DY_iX_i)=0. Таким образом, сумма всех слагаемых вида s₀(DX_iY_i), где X_iY_i лежит внутри треугольника T, равна 0.

Во втором случае, если сторона X_iY_i лежит на границе треугольника T, в сумму (23.5) входит лишь одно слагаемое вида s₀(DX_iY_i). Сгруппируем слагаемые вида s₀(DX_iY_i), для которых точки X_i и Y_i лежат на стороне AB треугольника T. Поскольку такие стороны X_iY_i составляют сторону AB, то в силу равенства (23.3), их сумма равна s₀(DAB). Аналогичные приведенному рассуждения показывают, что сумма слагаемых вида s₀(DX_iY_i), для которых точки X_i и Y_i лежат на стороне BC треугольника T равна s₀(DBC), а сумма слагаемых вида s₀(DX_iY_i), для которых точки X_i и Y_i лежат на стороне CA треугольника T равна s₀(DCA). Отсюда и из леммы 23.6 получим, что сумма, стоящая в правой части равенства (23.5) равна s₀(DAB)+s₀(DBC)+s₀(DCA)=s₀(ABC). Но из равенства (23.4) следует, что s(ABC)=s₀(ABC) и, поэтому, s(T)=s(T₁)+s(T₂)+...+s(T_m)=s(T₁)+s(T₂)+...+s(T_n). Лемма доказана полностью.

Из доказанной леммы несложно вывести теорему о существовании площади многоугольника.

Теорема 23.9 (Теорема существования площади многоугольника). Существует отображение s:R, удовлетворяющее аксиомам площади 1-4 определения 23.2.

Доказательство. Определим отображение s:R, положив для произвольного многоугольника M

s(M)=s(T₁)+s(T₂)+...+s(T_n), (23.6)

где M=T₁+T₂+...+T_n - произвольные разложения данного многоугольника на треугольники T₁, T₂,...,T_n.

Прежде всего, установим корректность принятого определения, т. е. независимость правой части равенства (23.6) от произвола выбора разложения M на треугольники. Пусть имеются два произвольных разложения M на треугольники: M=T₁+T₂+...+T_n и M=T₁+T₂+...+T_m. Покажем, что s(T₁)+s(T₂)+...+s(T_n)=s(T₁)+s(T₂)+...+s(T_m). Для этого воспользуемся следующей простой конструкцией “измельчения” данных разложений. Заметим, что пересечение двух любых треугольников, имеющих общие внутренние точки, является многоугольником, т. е. это пересечение можно разложить на сумму нескольких треугольников. Рассмотрим всевозможные попарные пересечения треугольников T_i и T_j, имеющих общие внутренние точки: U_ij=T_i T_j, i=1, ..., n; j=1, ..., m. Разложим каждый из этих многоугольников на треугольники, получим конечное множество, попарно не имеющих общих внутренних точек треугольников V₁, V₂,...,V_k. Нетрудно видеть, что каждый из треугольников T_i или T’_j, составлен⁵ из нескольких треугольников V_r и, поэтому, в силу леммы 23.8 равенства и имеют место для всех i=1, ..., n; j=1, ..., m. Суммируя первое из них по всем i=1, ..., n; а второе - по всем j=1, ..., m, получим равенство

s(T₁)+s(T₂)+...+s(T_n)=s(V₁)+s(V₂)+...+s(V_k)=s(T₁)+s(T₂)+...+s(T_m),

доказывающее корректность определения отображения s:R.

Покажем, что определенное равенством (23.6) отображения s:R удовлетворяет аксиомам 1-4 площади.

Так как. s(T)0 для любого треугольника T, то s(M)0 для любого многоугольника M и, поэтому, отображение s:R удовлетворяет аксиоме 1 определения 23.2.

Пусть имеются два конгруэнтных многоугольника MM. Это означает, что найдется движение g такое, что g(M)=g(M). Возьмем произвольное разложение многоугольника M на треугольники M=T₁+T₂+...+T_n, тогда, очевидно, M=T₁+T₂+...+T_n, где T_i=g(T_i) при всех i=1, ..., n. В силу определения 23.3, площади конгруэнтных треугольников равны: s(T_i)=s(T_i). Откуда в силу равенства (23.6) имеем: s(M)=s(T₁)+s(T₂)+...+s(T_n)=s(T₁)+s(T₂)+...+s(T_n)=s(M), что доказывает инвариантность отображения s:R для конгруэнтных многоугольников.

Пусть многоугольник M составлен из дух многоугольников M=M₁+M₂. Возьмем произвольные разложения многоугольников M₁ и M₂ на треугольники M₁=T₁+T₂+...+T_n, M₂=U₁+U₂+...+U_m. Очевидно, что M=T₁+T₂+...+T_n+U₁+U₂+...+U_m и, поэтому из (23.6) следует равенство s(M)=s(T₁)+s(T₂)+...+s(T_n)+s(U₁)+s(U₂)+...+s(U_m)=s(M₁)+s(M₂), доказывающее, что отображение s:R удовлетворяет аксиоме 3.

Проведем диагональ в единичном квадрате Q, получим два равнобедренных прямоугольных треугольника, катеты которых равны 1. Из определения 23.3 следует. что их площади равны . Из формулы (23.6) следует s(Q)=1/2+1/2=1, доказывающее, что отображение s:R удовлетворяет аксиоме 4 площади. Теорема доказана.

При доказательстве леммы 23.3, мы воспользовались тем, что треугольник и прямоугольник составлены из попарно конгруэнтных многоугольников. Отсюда мы сделали вывод, что их площади равны между собой. Ясно, что если два многоугольника служат объединением, с том смысле, в каком было указано в § 23, конечного числа попарно конгруэнтных многоугольников, то их площади равны между собой (докажите это утверждение самостоятельно). В дальнейшем многоугольники с равными площадями, будем называть равновеликими. Естественно поставить вопрос, если два многоугольника равновелики, можно ли представить их как объединения попарно конгруэнтных многоугольников. Ответ на него будет получен в настоящем параграфе. Введем следующее определение.

Определение 24.1. Многоугольники A и B называются равносоставленными в том случае, когда существуют их разложения и на попарно конгруэнтные многоугольники .

Равносоставленные многоугольники A и B будем обозначать через AB. Равносоставленные многоугольники имеют одинаковые площади. Положительный ответ на вопрос, любые ли два равновеликих многоугольника являются равносоставленными, дает теорема Бойяи-Гервина, доказанная независимо друг от друга венгерским математиком Ф. Бойяи⁶ в 1832 г. и немецким математиком П. Гервиным в 1833 г.

Рассмотрим несколько вспомогательных утверждений.

Лемма 24.1. Любой треугольник равносоставлен с некоторым прямоугольником.

Справедливость этого утверждения непосредственно следует из доказательства леммы 23. 3 (см. § 23). Проверьте ее самостоятельно.

Следующая лемма устанавливает транзитивность отношения равносоставленности многоугольников.

Лемма 24.2. Если для произвольных многоугольников A, B, C имеет место AB и BC, то AC.