Приклад виконання роботи
Завдання для прикладу:
Як завдання для прикладу візьмемо мову, задану КС-Граматикою
G({if,then,else,a,:=,or,xor,and,(,),$},{S,F,E,D,C},P,S з правилами Р:
S
F;
F if E then T else F| if E then F | a := E
T if E then T else T|a := E
E E or D| E xor D| D
D D and C| C
C a| (E)
Жирним шрифтом у граматиці й у правилах виділені термінальні символи. Ця мова вже була використана для ілюстрації виконання лабораторних робіт № 2 і № 3.
Результатом прикладу виконання лабораторної роботи №4 буде генератор списку тріад. Перетворення списку тріад в асемблерний код розглянутий далі в прикладі виконання курсової роботи (див. главу «Курсова робота»).
Побудова схем су-перекладу
Всі операції, які можуть бути присутнім у вхідній програмі мовою, заданою граматикою G, за змістом (семантиці) можна розділити на наступні групи:
логічні операції (or,xor,and);
оператор присвоювання;
повний умовний оператор (if... then ...else...) і неповний умовний оператор (if... then...);
операції, що не несуть змістовного навантаження, а служать тільки для створення синтаксичних конструкцій вихідної програми (у даній мові таких операцій дві: круглі дужки й крапка з комою).
Розглянемо схеми СУ-перекладу для всіх перерахованих груп операцій.
СУ-переклад для лінійних операцій
Лінійною операцією будемо називати таку операцію, для якої породжується код, що представляє собою лінійна ділянка результуючої програми. Наприклад, розглянуті раніше бінарні арифметичні операції (див. розділ «Короткі теоретичні відомості») є лінійними.
У заданій вхідній мові логічні операції виконуються над цілими десятковими числами як побітові операції, тобто вони також є бінарними лінійними операціями. Тому для них можуть бути використані ті ж самі схеми СУ-перекладу, що були розглянуті раніше.
ПРИМІТКА
Насправді можливий інший варіант обчислення логічних операцій у тому випадку, коли вони є операціями булевої логіки і їх операндами можуть бути тільки значення «Істина» (1) і «Брехня» (0). Тут цей варіант не розглядається. Більш докладно про нього сказано в розділі «Курсова робота», Коли будуються схеми СУ-перекладу для логічних операцій, а також можна звернеться до літератури [2].
СУ-переклад для оператора присвоювання
Оператор присвоювання також є бінарною логічною операцією, тому для нього може бути використана відповідна схема СУ-перекладу. Відмінність оператора присвоювання від інших бінарних лінійних операцій полягає в тім, що першим операндом у нього завжди повинна бути змінна. Тому функція, що будує код для оператора присвоювання, повинна перевіряти тип першого операнда. Ця перевірка являє собою реалізацію найпростішого семантичного аналізу й у цьому випадку необхідна, тому що присвоювання значень константам і відслідковується на етапі синтаксичного аналізу (про це було сказано в лабораторній роботі № 3).
СУ-переклад для умовних операторів
Для умовних операторів генерація коду повинна виконуватися в наступному порядку:
Породжується блок коду № 1, що обчислює логічний вислів, що перебуває між лексемами if (перша низлежача вершина) і then (третя низлежача вершина), - для цього повинна бути рекурсивно викликана функція породження коду для другої низлежачої вершини.
Породжується команда умовного переходу, що передає керування залежно від результату обчислення логічного вираження:
у початок блоку коду № 2. якщо логічне вираження має ненульове значення:
у початок блоку коду № 3 (для повного умовного оператора) або в кінець оператора (для неповного умовного оператора), якщо логічний вислів має нульове значення.
3.Породжується блок коду № 2, що відповідає операціям після лексеми then (третя низлежача вершина), - для цього повинна бути рекурсивно викликана функція породження коду для четвертої низлежачої вершини.
Для повного умовного оператора породжується команда безумовного переходу в кінець оператора.
Для повного умовного оператора породжується блок коду № 3. відповідним операціям після лексеми else (п'ята низлежача вершина), -для цього повинна бути рекурсивно викликана функція породження коду для шостої низлежачої вершини.
Схеми СУ-перевода для повного і неповного умовних операторів представлені на мал. 4.1.
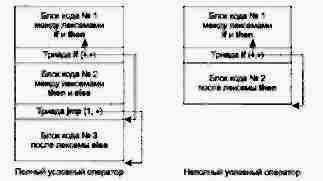
Рис. 4.1. Схеми СУ-перекладу для умовних операторів
Для того щоб реалізувати ці схеми, необхідні два типи тріад: тріада умовного переходу й тріада безумовного переходу.
Ці два типи тріад реалізуються в такий спосіб:
if(<операнд1>,<операнд2>) - тріада умовного переходу;
JMP(1.<операнда2>) - тріада безумовного переходу.
У тріади IF перший операнд може бути змінною, константою або посиланням на іншу тріаду, другий операнд - завжди посилання на іншу тріаду. Тріада IF передає керування на тріаду, зазначену другим операндом, якщо перший операнд дорівнює нулю, інакше керування передається на наступну тріаду.
У тріади JМР перший операнд не має значення (для визначеності він завжди буде дорівнює 1), другий операнд - завжди посилання на іншу тріаду. Тріада JМР завжди передає керування на тріаду, зазначену другим операндом.
СУ-переклад для семантично ненавантажених конструкцій
Операції, які не несуть ніякого значеннєвого навантаження, не вимагають побудови результуючого коду. Для них не потрібно будувати схеми СУ-перекладу.
Проте функція генерації списку тріад повинна обробляти й ці операції. Вони повинні оброблятися в такий спосіб:
для вершини, у якої перша низлежача вершина - відкриваюча дужка, друга низлежача вершина - вузол дерева (не кінцева вершина) і третя низлежача вершина - закриваюча дужка, повинна рекурсивно викликатися функція породження коду для другої низлежачої вершини;
для вершини, у якої перша низлежача вершина - вузол дерева (не кінцева вершина) і друга низлежача вершина - крапка з комою, повинна рекурсивно викликатися функція породження коду для першої низлежачої вершини.
Приклад генерації списку тріад
Візьмемо як приклад вхідний ланцюжок:
if а and b or a and b and 345 then a:= 5 or 4 and 7;
У результаті лексичного й синтаксичного розбору цього вхідного ланцюжка буде побудоване дерево синтаксичного розбору, наведене на мал. 4.2. Цьому дереву буде відповідати наступна послідовність тріад:
1: and (a,b)
2: and (a,b)
3: and (^2,345)
4: or (^1,^3)
5: if (^4,^9)
6: and (4,7)
7: or (5,^6)
8: :=(a,^7)
9: . . .
У цій послідовності дві лінійних ділянки: від тріади 1 до тріади 5 і від тріади 6 до тріади 9.
Після оптимізації методом згортки об'єктного коду одержимо послідовність тріад:
1: and (a,b)
2: and (a,b)
3: and (^2,345)
4: or (^1,^3)
5: if (^4,^9)
6: С (4,0)
7: С (5,0)
8: :=(a,5)
9: . . .
Якщо видалити тріади типу С, то ця послідовність прийме наступний вид:
1: and (a,b)
2: and (a,b)
3: and (^2,345)
4: or (^1,^3)
5: if (^4,^9)
6: :=(a,5)
7: . . .
Рис. 4.2. Дерево синтаксичного розбору ланцюжка
if а and b or a and b and 345 then a:= 5 or 4 and 7
Після оптимізації методом виключення зайвих операцій одержимо послідовність тріад:
1: and (a,b)
2: same (^1,0)
3: and (^1,345)
4: or (^1,^3)
5: if (^4,^7)
6: :=(a,5)
7: . . .
Якщо видалити тріади типу same, то ця послідовність прийме наступний вигляд:
1: and (a,b)
2: and (^2,345)
3: or (^1,^2)
4: if (^3,^6)
5: :=(a,5)
6: . . .
Після застосування оптимізації одержуємо послідовність із п'яти тріад. Це на 37,5% менше, ніж у вихідній без застосування оптимізації послідовності, що складалася з восьми тріад. Отже, обсяг результуючого коду й час його виконання в цьому випадку скоротяться приблизно на 37,5% (слово «приблизно» зазначено тут тому, що різні тріади можуть породжувати різну кількість команд у результуючому коді, а тому співвідношення між кількістю тріад і між кількістю команд об'єктного коду можуть небагато розрізнятися).
Можна ще звернути увагу на те, що алгоритм оптимізації методом виключення зайвих операцій не враховує особливості виконання логічних й арифметичних операцій. Методами булевої алгебри послідовність операцій «а and b or a and b and 345» можна перетворити в «а and b» точно так само, як послідовність операцій «a*b + a*b*345» - і «a*b*346», що було б ефективніше, ніж варіанти, які будує алгоритм оптимізації методом виключення зайвих операцій. Але для таких перетворень потрібні алгоритми, орієнтовані на особливості виконання логічних і арифметичних операцій [1,2, 7].