3. Ряды Фурье

3.1. Периодические функции

Многие процессы, происходящие в природе и технике, обладают свойством повторяться через определенные промежутки времени. Такие процессы называются периодическими и математически описываются периодическими функциями. К таким функциям относятся sin(x), cos(x), sin(wx), cos(wx). Сумма двух периодических функций, например, функция вида , вообще говоря, уже не является периодической. Но можно доказать, что если отношение w₁/w₂ – число рациональное, то эта сумма есть периодическая функция.

Простейшие периодические процессы – гармонические колебания – описываются периодическими функциями sin(wx) и cos(wx). Более сложные периодические процессы описываются функциями, составными либо из конечного, либо из бесконечного числа слагаемых вида sin(wx) и cos(wx).

3.2. Тригонометрический ряд. Коэффициенты Фурье

Рассмотрим функциональный ряд вида:

. (1)

Этот ряд называется тригонометрическим; числа а₀,b₀,a₁,b₁,а₂,b₂…,a_n,b_n,… называются коэффициентами тригонометрического ряда. Ряд (1) часто записывается следующим образом:

. (2)

Так как члены тригонометрического ряда (2) имеют общий период , то и сумма ряда, если он сходится, также является периодической функцией с периодом .

Допустим, что функция f(x) есть сумма этого ряда:

. (3)

В таком случае говорят, что функция f(x) раскладывается в тригонометрический ряд. Предполагая, что этот ряд сходится равномерно на промежутке , можно определить его коэффициенты по формулам:

, , . (4)

Коэффициенты ряда, определенные по этим формулам, называются коэффициентами Фурье.

Тригонометрический ряд (2), коэффициенты которого определяются по формулам Фурье (4), называются рядом Фурье, соответствующим функции f(x).

Таким образом, если периодическая функция f(x) является суммой сходящегося тригонометрического ряда, то этот ряд является ее рядом Фурье.

3.3. Сходимость ряда Фурье

Формулы (4) показывают, что коэффициенты Фурье могут быть вычислены для любой интегрируемой на промежутке -периодической функции, т.е. для такой функции всегда можно составить ряд Фурье. Но будет ли этот ряд сходиться к функции f(x) и при каких условиях?

Напомним, что функция f(x), определенная на отрезке [a;b], называется кусочно-гладкой, если она и ее производная имеют не более конечного числа точек разрыва первого рода.

Следующая теорема дает достаточные условия разложимости функции в ряд Фурье.

Теорема Дирихле. Пусть -периодическая функция f(x) является кусочно-гладкой на . Тогда ее ряд Фурье сходится к f(x) в каждой ее точке непрерывности и к значению 0,5(f(x+0)+f(x-0)) в точке разрыва.

Пример1.

Разложить в ряд Фурье функцию f(x)=x, заданную на интервале .

Решение. Эта функция удовлетворяет условиям Дирихле и, следовательно, может быть разложена в ряд Фурье. Применяя формулы (4) и метод интегрирования по частям , найдем коэффициенты Фурье:

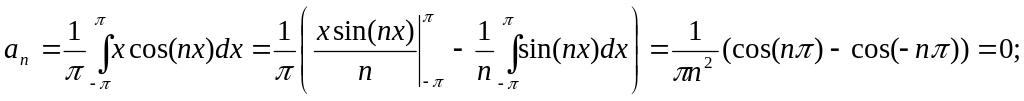
Т.к. .

Таким образом, ряд Фурье для функции f(x) имеет вид:

.