2. Функциональные ряды. Область сходимости функционального ряда

Рассмотрим последовательность функций, заданных на некотором промежутке [a,b]:

f₁(x), f₂(x), f₃(x) … f_n (x), ….

Приняв эти функции в качестве членов ряда, образуем ряд:

f₁(x) + f₂ (x) + f₃ (x) + … + f_n (x) + …, (1)

который называется функциональным рядом.

Например: sin(x) + sin(2x) + sin(3x) + … + sin(nx) + …

В частном случае функциональным рядом является ряд:

, (2)

который называется степенным рядом, где постоянные числа, называемые коэффициентами членов степенного ряда.

Степенной ряд может быть записан и в такой форме:

, (3)

где некоторое постоянное число.

При определенном фиксированном или числовом значении x получим числовой ряд, который может быть сходящимся или расходящимся.

Определение: Совокупность всех значений х (или всех точек х числовой прямой), при которых степенной ряд сходится, называется областью сходимости степенного ряда.

Пример 1.

Найти область сходимости степенного ряда:

.

Решение (1 способ).

Применим признак Даламбера.

Так как признак Даламбера применим к рядам только с положительными членами, то выражение, стоящее под знаком предела, взято по абсолютной величине.

.

По признаку Даламбера ряд сходится, если и .

Т.е. ряд сходится, если < 1, откуда или -3<x<3.

Получим интервал сходимости данного степенного ряда: (-3;3).

В крайних точках интервала x = , будем иметь .

В этом случае теорема Даламбера не дает ответа на вопрос о сходимости ряда.

Исследуем ряд на сходимость в граничных точках:

x = -3,

.

Получим знакочередующийся ряд. Исследуем его на сходимость по признаку Лейбница:

1. члены ряда, взятые по абсолютной величине, монотонно убывают.

2. Следовательно, ряд в точке x = -3 сходится.

x = 3,

.

Получим положительный ряд. Применим интегральный признак Коши сходимости ряда.

члены ряда монотонно убывают.

Функция на промежутке :

1. непрерывна;

2. f(x) > 0, т.е. (положительна);

3. монотонно убывает;

4. это значит, что функция является функцией, образующей ряд.

.

Несобственный интеграл расходится, значит, ряд в точке x=3 расходится.

Ответ: область сходимости ряда [-3;3).

Второй способ определения области сходимости степенного ряда основан на применении формулы радиуса сходимости степенного ряда:

, где и коэффициенты и членов ряда.

Для данного ряда имеем:

. R=3.

ряд сходится

Интервал сходимости ряда: -3<x<3.

Далее, как и в предыдущем случае, надо исследовать в граничных точках: x = .

Ответ: область сходимости ряда [-3;3).

Отметим, что второй способ определения области сходимости степенного ряда с использованием формулы радиуса сходимости ряда более рационален.

Пример 2.

Найти область сходимости степенного ряда: .

Найдем R – радиус сходимости ряда.

, , .

. .

Интервал сходимости ряда (- ; ).

Исследуем ряд на сходимость в точках x = - и x = .

x = - ,

.

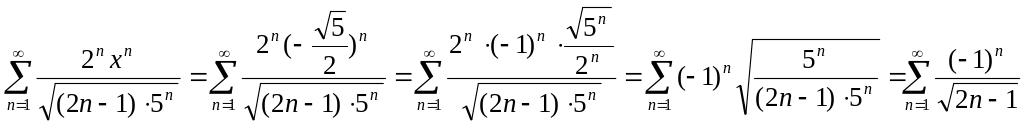Получим знакочередующийся ряд. Применим признак Лейбница:

1. члены ряда, взятые по абсолютной величине, монотонно убывают.

2. , следовательно, ряд в точке x = - сходится.

x = , .

Получили ряд с положительными членами. Применим интегральный признак Коши.

Здесь :

, члены ряда монотонно убывают.

Функция на промежутке :

1. непрерывна;

2. положительна;

3. монотонно убывает;

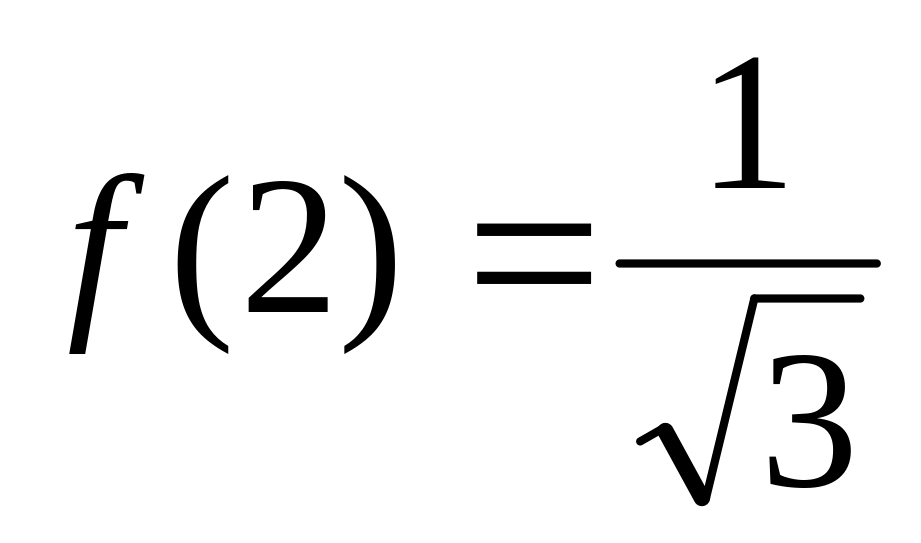4. , , , …. т.е. f(x) – функция, образующая ряд.

.

Несобственный интеграл расходится, ряд расходится.

Ответ: [- ; ) – область сходимости ряда.