1.4. Интегральный признак Коши сходимости ряда

Дан ряд с положительными членами u₁+u₂+…+u_n+… , члены которого монотонно убывают, т.е. u_n+1 < u_n.

Составим непрерывную невозрастающую положительную функцию f(x), заданную на такую, что при x = 1,2,3,…,n,… значение функции равно соответствующему члену ряда. Функция f(x) называется производящей функцией данного ряда.

Теорема. Если члены данного ряда монотонно убывают (u_n+1 < 0 u_n , n = 1,2, 3, …) и если функция y = f(x) при непрерывна, положительна и монотонно убывает, и f(n)=u_n, тогда

1. если 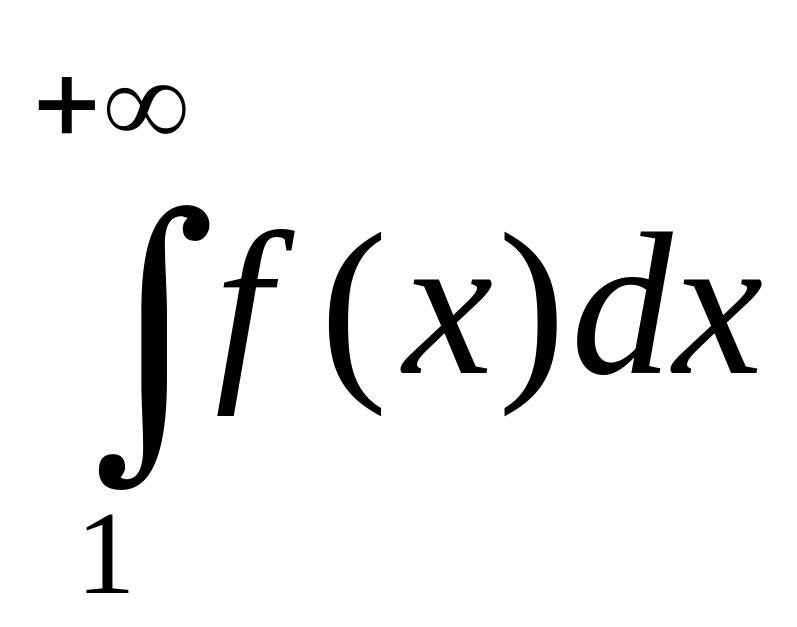сходится, то сходится и данный ряд;

2. если расходится, то расходится и данный ряд.

Пример 1.

Исследовать на сходимость ряд: .

Составим производящую функцию ряда . Вычислим несобственный интеграл этой функции:

.

Несобственный интеграл сходится, сходится и данный ряд.

Пример 2.

Исследовать сходимость числового ряда: .

Составим производящую функцию ряда . Вычислим:

Несобственный интеграл сходится, сходится и данный ряд.

Пример 3.

Исследовать сходимость ряда: .

Составим производящую функцию ряда . Вычислим:

Несобственный интеграл расходится, расходится и данный ряд.

1.5. Знакочередующиеся ряды. Теорема Лейбница

Ряд называется знакочередующимся, если любые два соседних его члена имеют разные знаки, т.е. ряды вида u₁ – u₂ + u₃ – u₄ +… + u_n + …, где u₁, u₂, …, u_n, … положительны.

Теорема Лейбница. Если члены знакочередующегося ряда, взятые по абсолютной величине, монотонно убывают и модуль общего члена ряда стремится к нулю при , т.е. , то ряд сходится.

Пример 1.

Исследовать сходимость знакочередующегося ряда:

.

Члены ряда, взятые по абсолютной величине, монотонно убывают:

Ряд сходится.

1.6. Знакопеременные ряды. Абсолютная и условная сходимость ряда

Ряд u₁+u₂+…+u_n+… называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.

Знакочередующиеся ряды являются частным случаем знакопеременных рядов.

Теорема. Дан знакопеременный ряд u₁+u₂+…+u_n+…(1). Составим ряд |u₁|+|u₂|+…+|u_n|+… (2). Если ряд (2), составленный из абсолютных величин членов ряда (1), сходится, то ряд (1) сходится.

Определение. Знакопеременный ряд u₁+u₂+…+u_n+… называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов |u₁|+|u₂|+…+|u_n|+… .

Если же знакопеременный ряд (1) сходится, а ряд (2), составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд (1) называется условно или неабсолютно сходящимся рядом.

Пример 1.

Исследовать на сходимость и абсолютную сходимость ряд: .

Знакочередующийся ряд сходится по теореме Лейбница, т.к. . Члены ряда монотонно убывают и . Теперь исследуем данный ряд на абсолютную сходимость. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: . Исследуем сходимость этого ряда с помощью признака Даламбера: . Ряд сходится. Значит, заданный знакочередующийся ряд сходится абсолютно.

Пример 2.

Исследовать на сходимость и абсолютную сходимость ряд: .

По теореме Лейбница . Ряд сходится. Ряд, составленный из абсолютных величин членов данного ряда, имеет вид . По признаку Даламбера получим . Ряд сходится, значит, заданный знакопеременный ряд сходится абсолютно.