Эффект Холла

Для непосредственного определения концентрации носителей заряда в полупроводниках используют эффект Холла

Рассмотрим полупроводнике n-типа проводимости.

Ч

Рис.3.22. ЭДС Холла V_H (а) и угол Холла φ (б)

ерез образец пропускают токI вдоль оси х. Магнитное поле с индукцией направлено вдоль осиу. Под действием силы Лоренца носители заряда отклоняются по осиz. На верхней грани накапливается отрицательный заряд свободных носителей (n>p), на нижней грани - положительный заряд ионов примеси. Разделение зарядов приводит к возникновению электрического поля Холла .Поле E_H растет до тех пор, пока не скомпенсирует действие силы Лоренца. При этом ток I_z=0, а результирующее поле повернуто относительно внешнего поля E_x на угол Холла φ.

(3.32_25)

где _H - холловская подвижность, которая отличается от дрейфовой подвижности .

По определению

, (3.33_26)

где τ - время релаксации, а знак означает усреднение τ по энергии;- эффективная масса носителя заряда.

Дырки и электроны смещаются в одну и ту же сторону, так как направления дрейфовой скорости и знаки заряда частицe противоположны.

Для слабого магнитного поля (µ_HB)²<<1

(3.34_27)

где R_H - постоянная Холла; j_x - плотность тока в образце.

Для Si, Ge, GaAs к слабым полям относятся магнитные поля с индукцией В<(0.5 – 1.0) Тл. Тогда для R_H получим следующее выражение.

. (3.35_28)

Отношение называется Холл-фактором.

В слабых магнитных полях при Холл-фактор r зависит от механизма рассеяния. При рассеянии на ионах примеси, что обычно имеет место в области низких температур, r=1.93. При рассеянии на фононах (при более высоких температурах) r=1.18. В невырожденном полупроводнике в слабом магнитном поле r составляет (1  1.93), в сильном магнитном поле Холл-фактор r=1. В металлах и вырожденных полупроводниках r=1.

В сильных магнитных полях при (µ_HB)²>>1 r=1 и не зависит от механизма рассеяния.

Для кремния, германия и арсенида галлия к слабым полям относятся магнитные поля с индукцией В<(0.5 – 1.0) Тл.

Для полупроводников n-типа R_H<0, для полупроводников р-типа R_H>0.

Для полупроводников со смешанной проводимостью

, (3.36_29)

где .

Температурные зависимости коэффициента Холла для невырож-денных примесных полупроводниковn–типа проводимости и p–типа проводимости различны. В электронном полупроводнике знак коэффициента Холла R_H(T) отрицателен во всем диапазоне температур, и убывает с ростом температуры.

В дырочном полупроводнике знак R_H(T)>0 вплоть до температур, отвечающих переходу в область собственной проводимости, когда коэффициент Холла, продолжая уменьшаться, проходит через нуль и меняет знак. Поэтому по экспериментальной кривой R_H(T) в соответствующем интервале темпера-тур можно определить тип прово-димости полупроводника.

R_H меняет знак не при переходе к собственной проводимости, когда p=n, при а p=nb². Для при комнатной температуре b=80, и в собственном полупроводнике R_H отрицательна, как и в полупроводнике n-типа проводимости. Именно это обстоятельство приводит в InSb p-типа проводимости к холловскому выбросу выше прямой, соответствующей собственной проводимости. То же обнаруживается и для температурной зависимости ρ в образцах p-типа проводимости. Максимум удельного сопротивления наблюдается не при p=n=n_i, а при . Еслиb=80, то это почти на порядок величины больше n_i, и максимальное значение удельного сопротивления в раз больше, чем для собственного полупроводника.

Вэксперименте задают плотность токаj_x и магнитную индукцию В и измеряют напряжение Холла . Зная геометрию образца, можно рассчитать постоянную ХоллаR_H и определить концентрацию свободных носителей n. Подвижность Холла вычисляют по формуле.

, (3.37_30)

где σ - проводимость образца. Величину (гдеl - расстояние между контактами 1 и 3) находят, используя измеренные значения V_ρ.

В образце со смешанной проводимостью определить концентрации p и n и подвижности μ_p и μ_n раздельно с помощью эффекта Холла невозможно.

Если в образце концентрация носителей заряда распределена неоднородно, то могут быть определены такие параметры слоя, как удельная слоевая электропроводность , слоевой коэффициент Холла , слоевая концентрация носителей заряда и слоевая подвижность , которыеопределяются следующими соотношениями.

. (3.38_31)

. (3.39_32)

. (3.38_33)

. (3.39_34)

При измерении ЭДС Холла следует учитывать физические эффекты, которые могут исказить результаты и привести к систематическим и случайным ошибкам.

1. Эффект Эттинсгаузена - поперечный термогальваномагнитный эффект. Магнитное поле действует на электроны с большей энергией ("быстрые" электроны) с большей силой, чем на "медленные". Поэтому происходит разделение носителей по скоростям (по энергиям). При взаимодействии с решеткой возникает градиент температурыи соответствующая термоЭДСV_E. Изменение направления 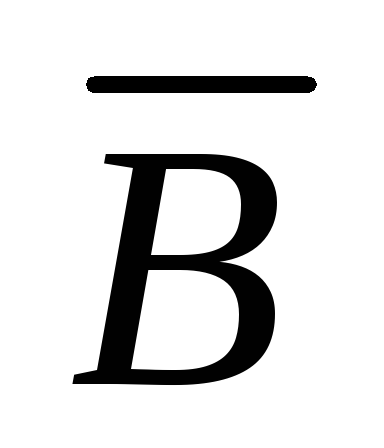илиприводит к такому же изменению знака термоЭДСV_E, что и ЭДС Холла V_H, (см. таблицу).

2. Часто в процессе измерений возникает градиент температуры 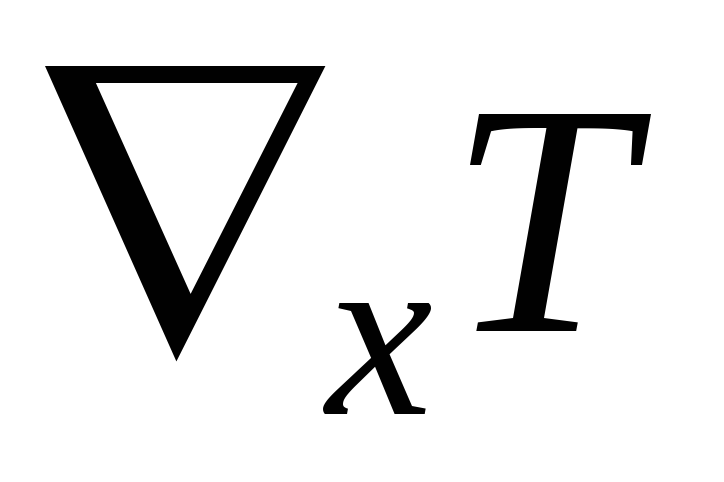вдоль оси x. Это связано либо с несовершенством нагревателя, либо с неоднородным выделением джоулева тепла при прохождении тока I через контакты. В этих условиях появляются дополнительные ЭДС.

3. Эффект Нернста - Эттинсгаузена - термогальванический эффект. Если есть градиент температуры , возникает диффузионный поток электронов, который отклонятся магнитным полемВ так же, как в эффекте Холла отклоняется дрейфовый поток. При этом появляется ЭДС V_N, вдоль оси z. Знак ЭДС зависит от направления и не зависит от направления.

4. Эффект Риги - Ледюка - термомагнитный эффект. Он аналогичен эффекту Эттинсгаузена, но только в отношении носителей диффузионного тока, обусловленного . Разделение "быстрых" и "медленных"носителей вызывает появление 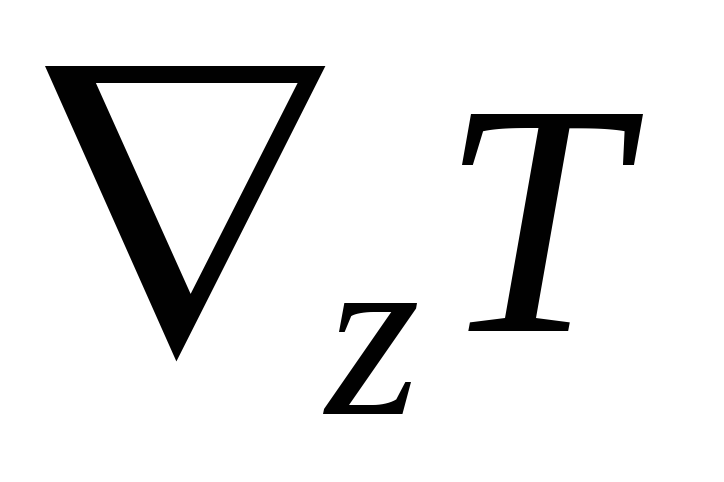и соответствующей термоЭДСV_RL. Знак ЭДС зависит от полярности поля и не зависит от знака токаI.

5. Дополнительная разность потенциалов на холловских контактах может возникать, если они несколько смещены относительно друг друга вдоль осих. При измерении полярности тока ЭДСменяет знак, а от полярности поляне зависит.

Эффектом магнитосопротивления в слабом магнитном поле можно пренебречь, так как это эффект второго порядка малости .

Изменения знака ЭДС в зависимости от изменения полярности тока и магнитного поляпредставлены в таблице.

Таблица