Упражнение 11. Приведение уравнения кривой второго порядка к каноническому виду.

• Привести уравнение кривой второго порядка к каноническому виду с помощью поворота и/или параллельного переноса системы координат.

• Отметить в старой системе координат центр кривой и направление осей новой системы координат.

• Построить кривую. Дать название.

• В случае, если это эллипс, гипербола, сопряженная гипербола или парабола, найти ее характеристики (центр, вершины, фокусы, уравнения директрис) относительно старой системы координат. Фокусы и директрисы также отметить на рисунке.

А) Б)В)Упражнение 12 а*. Приведение уравнения кривой второго порядка к каноническому виду.

Для уравнения кривой второго порядка реализоватьm-функциюget_canonical, которая приводит уравнение данной кривой к каноническому виду, используя поворот осей координат на определенный угол. Таким образом, заголовок файла «get_canonical.m» будет выглядеть примерно так:function [u,v,phi]= get_canonical (a,b,c)

Упражнение 12 б*. Приведение уравнения кривой второго порядка к каноническому виду.

• Нарисовать кривую, заданную уравнением .

• С помощью реализованной ранее функции get_canonicalпривести уравнение данной кривой к каноническому виду, отметить фокусы, отобразить директрисы. Сравнить результат.

5. Поверхности второго порядка.

Параметрическое задание поверхностей второго порядка

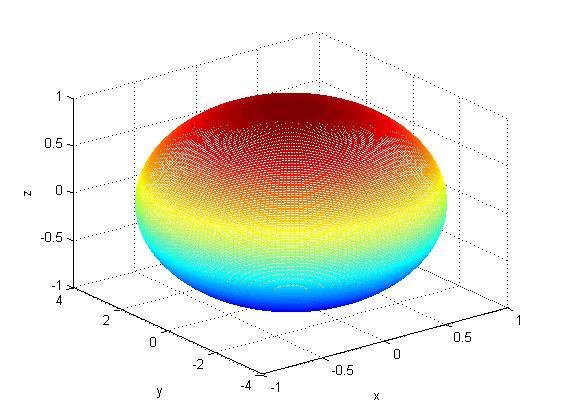
Эллипсоид

уравнение этой поверхности можно задать параметрически:

Каждой точке на поверхности эллипсоида с координатами тавится в соответствии пара чисел-координатпо формулам:

.

сли то мы получим часть эллипсоида лежащего в первом октанте(

ли то мы получим верхнюю часть эллипсоидаЕслито мы получим весь эллипсоид.

θ – греческая буква «тетта», φ – греческая буква «фи».

Пример построения эллипсоида:

a=1;

b=4;

c=1;

theta=(-pi/2:pi/200:pi/2)';

phi=0:pi/100:2*pi;

x=a*cos(theta)*cos(phi);

y=b*cos(theta)*sin(phi);

z=c*sin(theta)*ones(size(phi));

figure ('Color','w')

mesh(x,y,z);

xlabel('x'), ylabel('y'),zlabel('z')

В этой программе мы транспонировали строку - массив «theta», так как для каждого аргумента функции «mesh» мы создадим квадратные матрицыmesh(x(i,j),y(i,j),z(i,j)), а при перемножении столбца на строку как раз и получается квадратная матрица.

a=1;

b=4;

c=1;

Упражнение 13.

Используя данную программу изобразите часть эллипсоида лежащего в первом октанте (,ерхнюю часть эллипсоидаизобразите также эллипсоид в декартовых координатах, используя«meshgrid» и «mesh» или «plot3». Сравните полученные результаты.

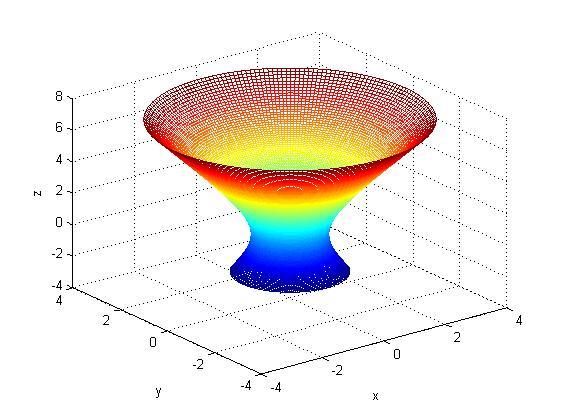
Однополостный гиперболоидпределяется следующей зависимостью координат точек поверхностит двух параметров.

» «»иперболические косинус и синус. Параметрегулирует высоту фигуры вдоль осиOZ. Для того чтобы при подстановке этих параметрических уравнений в уравнение однополостного гиперболоида получить тождество, нужно вспомнить аналог основного тригонометрического тождества для гиперболических функцийПример построения однополостного гиперболоида:

a=1;

b=1;

c=2;

u=(-1:0.02:2)';

phi=0:0.01*pi:2*pi;

X=a*cosh(u)*cos(phi);

Y=b*cosh(u)*sin(phi);

Z=c*sinh(u)*ones(size(phi));

figure('Color','w')

mesh(X,Y,Z);

xlabel('x'), ylabel('y'),zlabel('z')

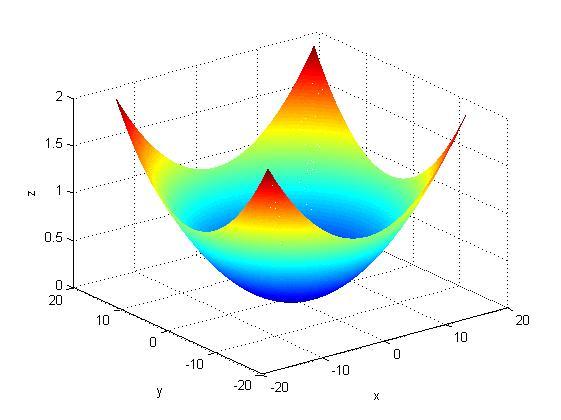
Каноническое уравнение эллиптического параболоидаимеет видТак как переменнаяzявно выражена черезxиy, то эллиптический параболоид можно построить с помощью«meshgrid»

a=16;

b=16;

[X,Y]=meshgrid(-a:0.1:a,-b:0.1:b);

Z=(X.^2/a^2 +Y.^2/b^2 );

figure('Color','w')

mesh(X,Y,Z);

xlabel('x'), ylabel('y'),zlabel('z')