
coll_1_2015
.docВопросы к коллоквиуму по математическому анализу
1 семестр
МП-10, 11, 12, 13, 14, 15
-
Логическая символика. Отрицание высказываний.
-
Ограниченные и неограниченные множества. Верхние и нижние грани.
-
Точные верхние и нижние грани множества. Эквивалентные определения.
-
Свойства точных граней.
-
Теорема о существовании точной верхней грани ограниченного множества.
-
Определение предела последовательности. Предельные точки. Единственность предела.
-
Ограниченность сходящейся последовательности.
-
Сохранение знака сходящейся последовательности.
-
Предельный переход под знаком неравенства для последовательностей.
-
Лемма о двух милиционерах для последовательностей.
-
Бесконечно малые последовательности. Связь с пределом последовательности. Бесконечно большие последовательности. Связь между бесконечно большими и бесконечно малыми последовательностями.
-
Свойства бесконечно малых последовательностей ( с помощью определения)..
-
Теоремы о сумме и произведении сходящихся последовательностей.
-
Теорема о частном сходящихся последовательностей.
-
Предел монотонной ограниченной последовательности.
-
Бином Ньютона (без доказательства). Число "е".
-
Лемма о вложенных отрезках.
-
Теорема Больцано-Вейерштрасса.
-
Критерий Коши сходимости последовательности.
-
Предел функции в точке. Эквивалентность определений по Коши и по Гейне. Примеры функций, имеющих и не имеющих предела в точке.
-
Ограниченность функции, имеющей конечный предел.
-
Сохранение знака функции, имеющей конечный ненулевой предел.
-
Предельный переход под знаком неравенства для функций.
-
Лемма о двух милиционерах для функций
-
Арифметические действия над пределами функций.
-
Первый замечательный предел.
-
Второй замечательный предел.
-
Критерий Коши существования предела функции.
-
Непрерывность функции в точке. Свойства. Теорема о непрерывности сложной функции.
-
Непрерывность основных элементарных функций.
-
Бесконечно малые и бесконечно большие функции. Пределы на бесконечности.
-
Определения «о»-малого, эквивалентных функций. Вычисление пределов с помощью эквивалентностей.
-
Теорема об ограниченности непрерывной на отрезке функции.
-
Теорема о максимальном и минимальном значении непрерывной на отрезке функции.
-
Теорема о переходе через 0 непрерывной на отрезке функции.
-
Теорема о промежуточных значениях непрерывной на отрезке функции.
-
Теорема о функции, обратной непрерывной монотонной.
-
Односторонние пределы. Классификация точек разрыва. Существование односторонних пределов у монотонных на отрезке функций.
-
Модуль непрерывности. Равномерная непрерывность.
-
Равномерная непрерывность функции на отрезке.
Упражнения к коллоквиуму по математическому анализу
1 семестр
МП-10, 11, 12, 13, 14, 15
-
Доказать, что если существуют
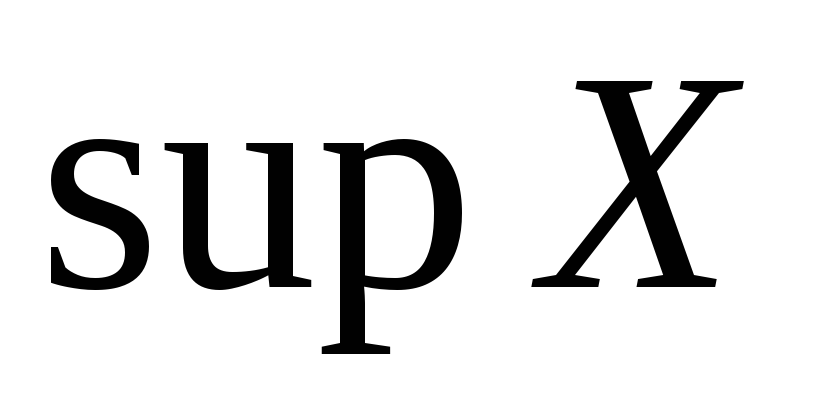 и
и
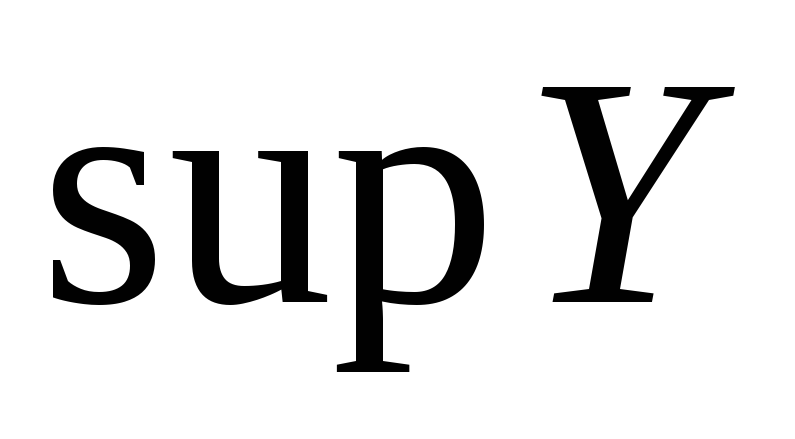 ,
то существует
,
то существует
 и
и
 (по
определению).
(по
определению). -
Доказать, что если существуют
 и
и
 ,
то существует
,
то существует
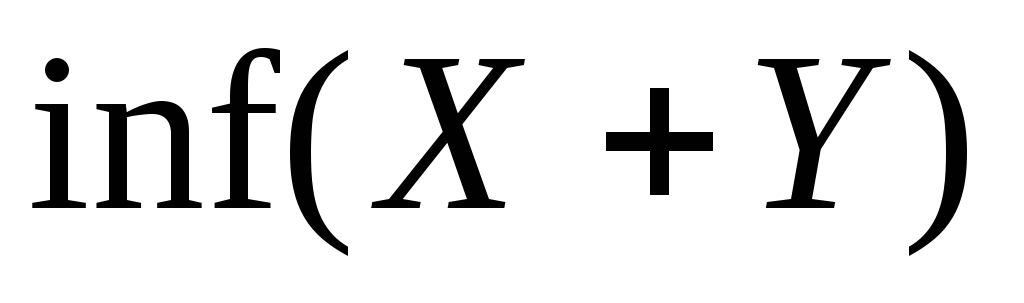 и
и
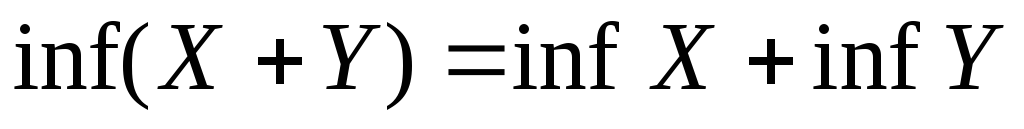 (
по определению).
(
по определению). -
Доказать, что если существует
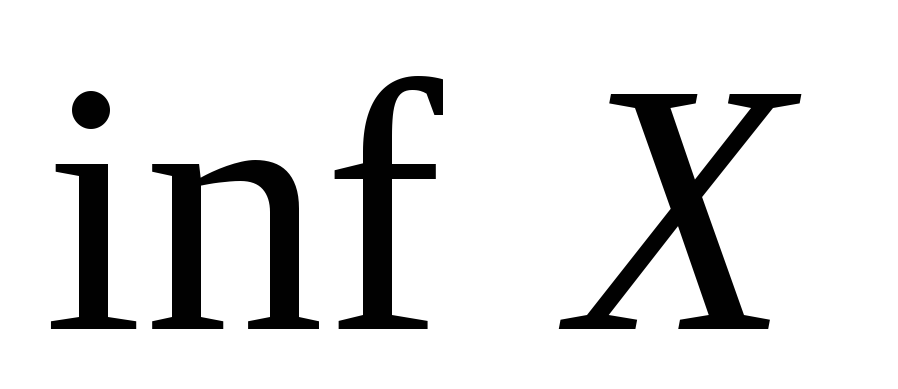 , то существует
, то существует
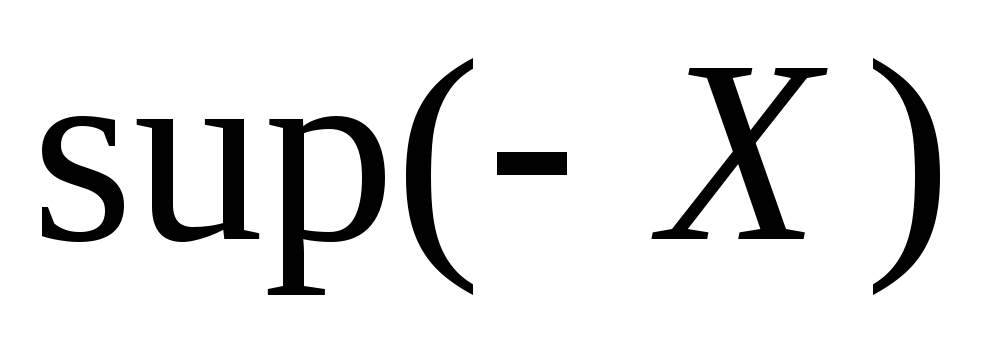 и
и
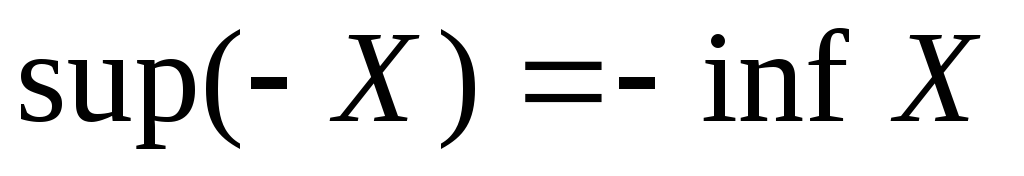 (по определению
(по определению -
Доказать, что если существует
 ,
то существует
,
то существует
 и
и
 (
по определению).
(
по определению). -
Доказать, что если
 и существуют
и существуют
 ,
,
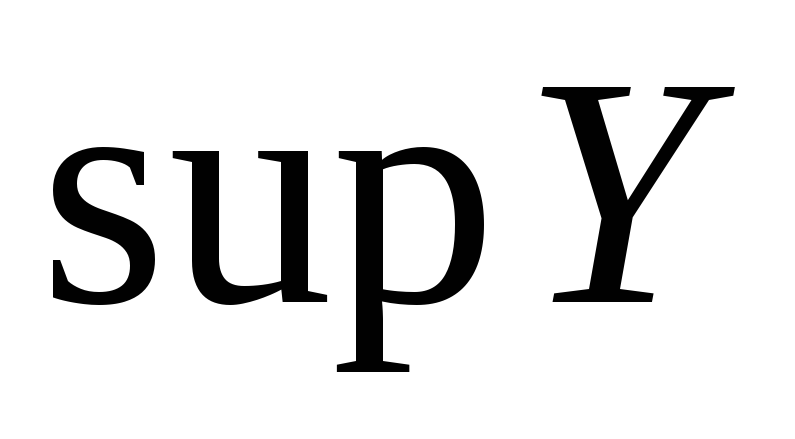 ,
то
,
то
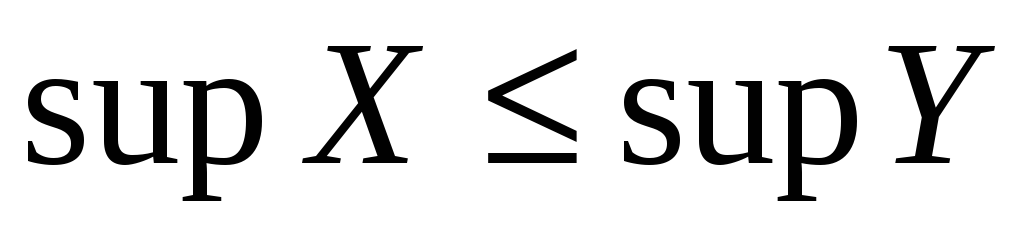 (
по определению).
(
по определению). -
Доказать, что если
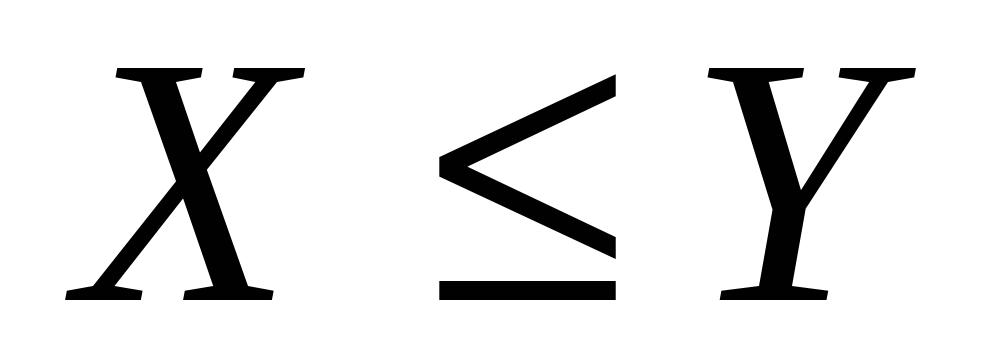 и существуют
и существуют
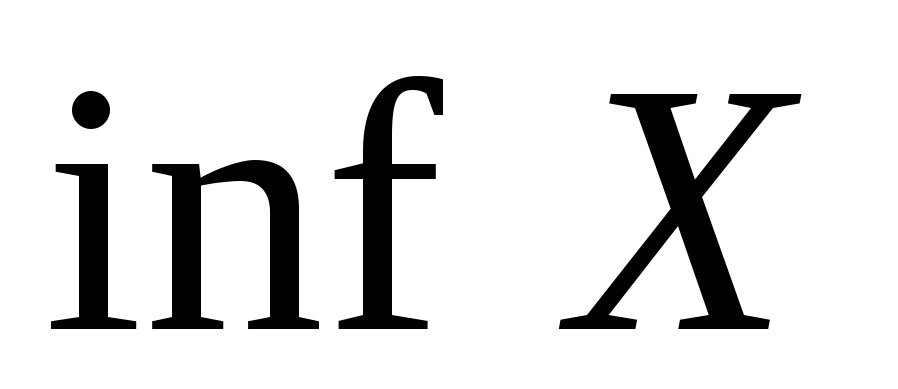 и
и
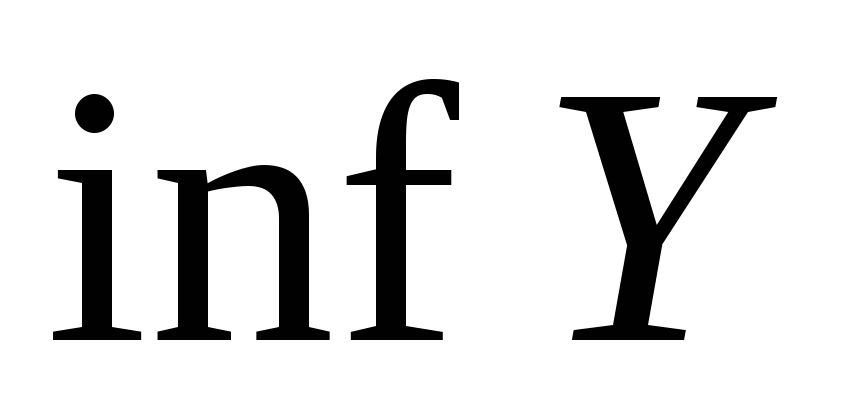 ,
то
,
то
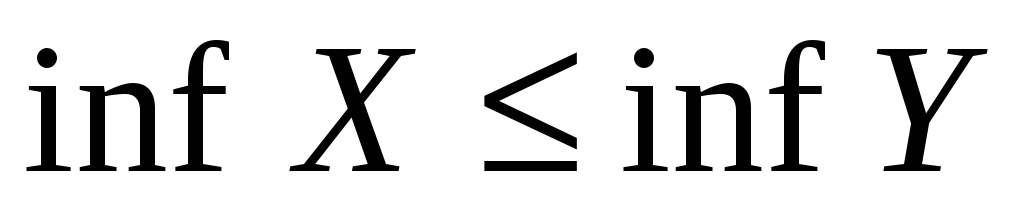 (
по определению).
(
по определению). -
Доказать, что если
 и существуют
и существуют
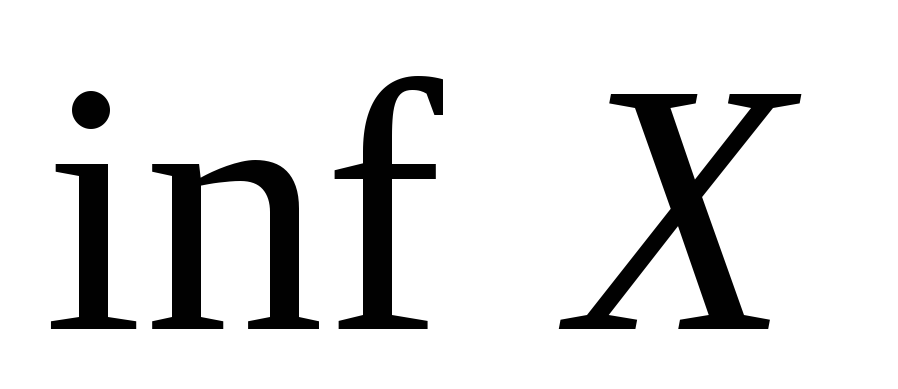 и
и
 ,
то
,
то
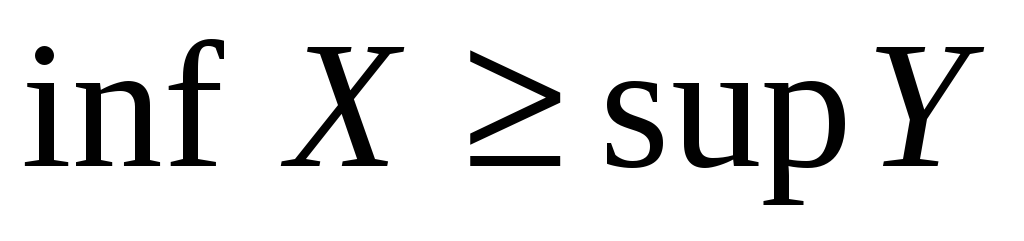 (
по определению).
(
по определению). -
Доказать, что у ограниченного снизу множества существует
 (непосредственно).
(непосредственно). -
Если в любой окрестности точки а лежит бесконечное множество членов последовательности, следует ли, что она
а) сходится;
б) ограничена?
-
Может ли неограниченная последовательность иметь предельную точку?
-
Может ли бесконечно большая последовательность иметь предельную точку?
-
Верно ли утверждение: "Если последовательность имеет одну предельную точку, то она сходится"?
-
Доказать
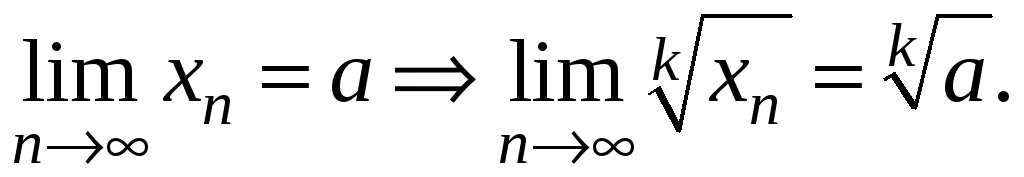
-
Доказать, что функция Дирихле
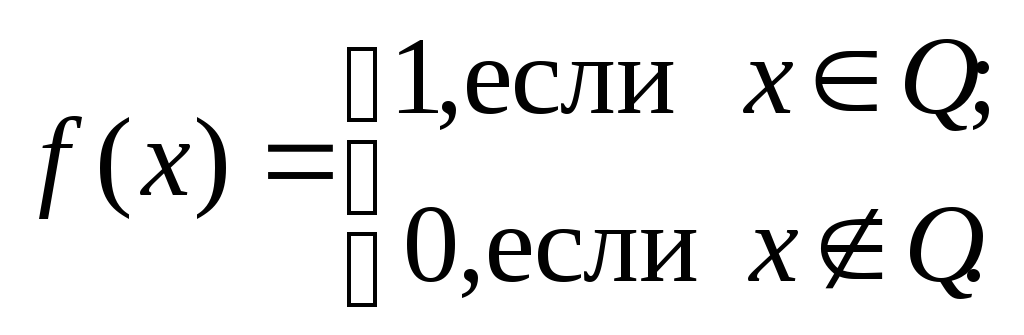 не имеет предела ни в одной точке (по
определениям по Коши и по Гейне, по
критерию Коши)..
не имеет предела ни в одной точке (по
определениям по Коши и по Гейне, по
критерию Коши).. -
Доказать, что функция
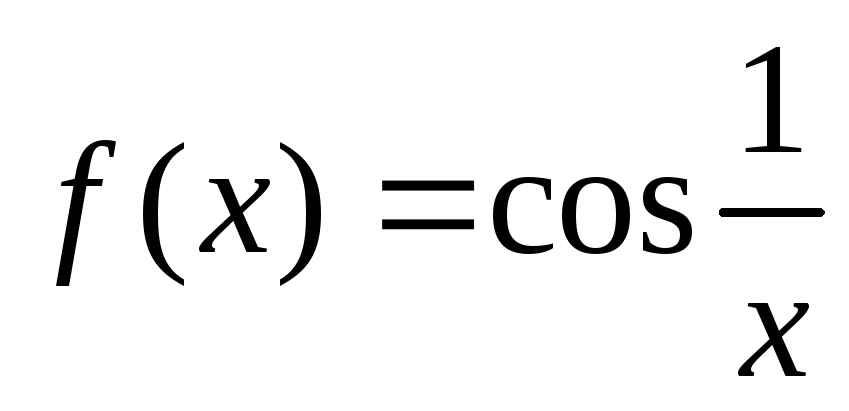 не имеет ни правого, ни левого предела
в точке
не имеет ни правого, ни левого предела
в точке
 .
. -
Доказать по определению непрерывность функций
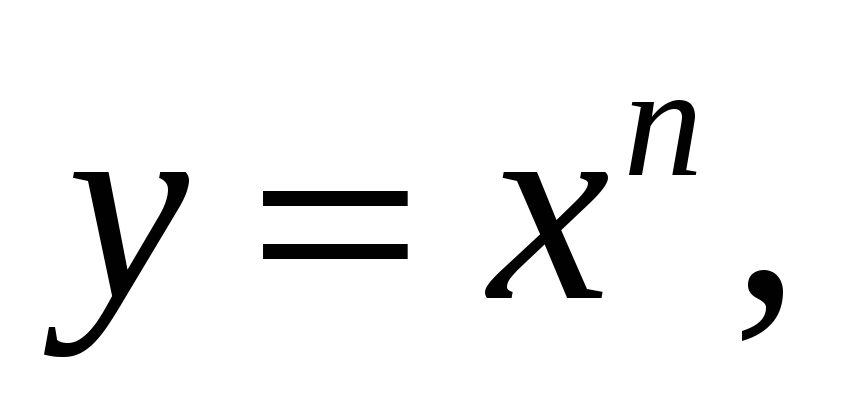
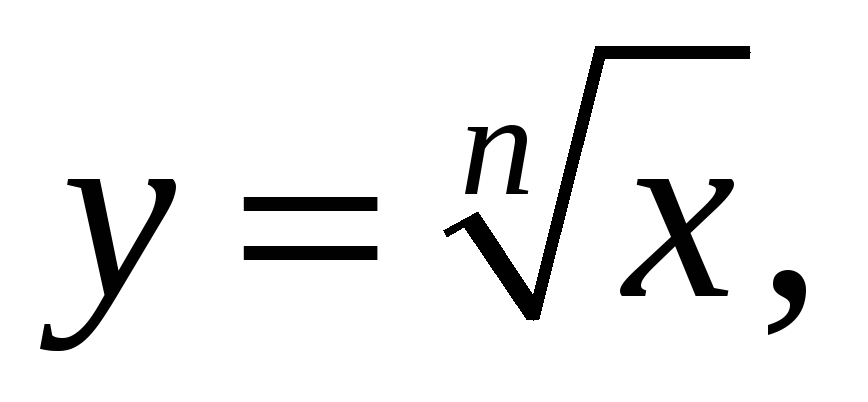


 в точке
в точке

-
Исходя из определения "о-малого" доказать
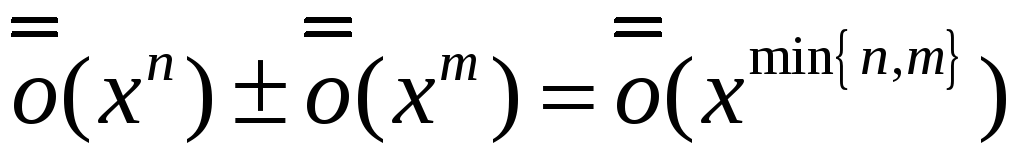 .
. -
Исходя из определения "о-малого" доказать
 .
. -
Исходя из определения "о-малого" доказать
 .
. -
Обосновать вычисление предела
 если
если
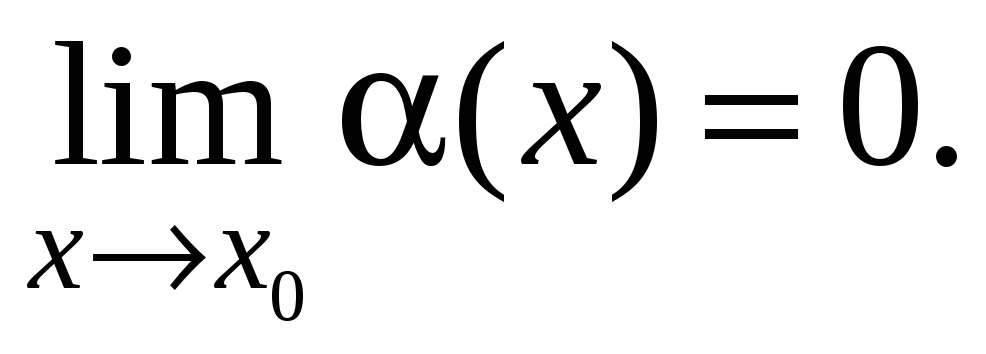
-
Обосновать вычисление предела
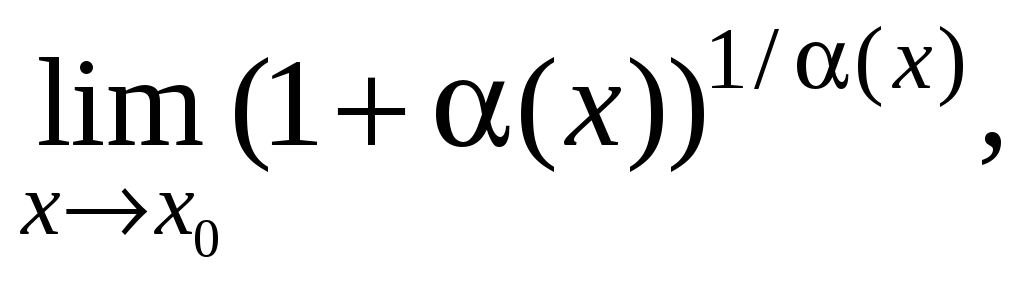 если
если
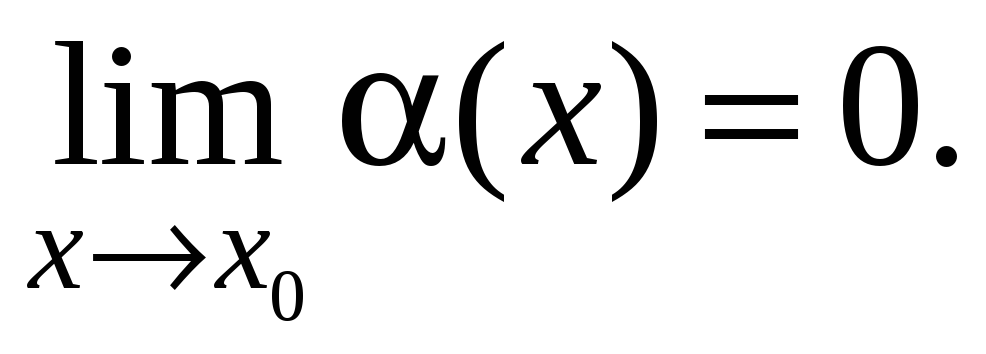
-
Доказать, что монотонная неограниченная последовательность является бесконечно большой.
-
Доказать, что из неограниченной последовательности можно выделить бесконечно большую.
Допуск к коллоквиуму
Расписать по определению по Коши и по Гейне, символами и словами, нарисовать картинку, обозначив соответствующие окрестности для случаев:
1.
![]() ;
2.
;
2.
![]() ;
3.
;
3.
![]() ;
4.
;
4.
![]() ;
;
5.
![]() ;
6.
;
6.
![]() ;
7.
;
7.
![]() ;
8.
;
8.
![]() ;
;
9.
![]() ;
10.
;
10.
![]() ;
11.
;
11.
![]() ;
12.
;
12.
![]() ;
;
13.
![]() ;
14.
;
14.
![]() ;
15.
;
15.
![]() ;
16.
;
16.
![]() ;
;
17.
![]() ;
18.
;
18.
![]() ;
19.
;
19.
![]() ;
20.
;
20.
![]() ;
;
21.
![]() ;
22.
;
22.
![]() ;
23.
;
23.
![]() ;
24.
;
24.
![]() .
.
