Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебники по PCAD / Автоматизация проектирования РЭС_Топологическое проектирование печатных плат_Кофанов_2008.pdf

Скачиваний:

135

Добавлен:

27.03.2016

Размер:

3.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.5.Математические модели схем

1.5

0.5

1.5

0.5

R= e3

0.5

1.5

0.5

1.5

0 .

4.6. Математические модели монтажного пространства

Под монтажным пространством типовой конструкции радиоэлектрон-

ной аппаратуры понимают метрическое пространство, в котором устанавли-

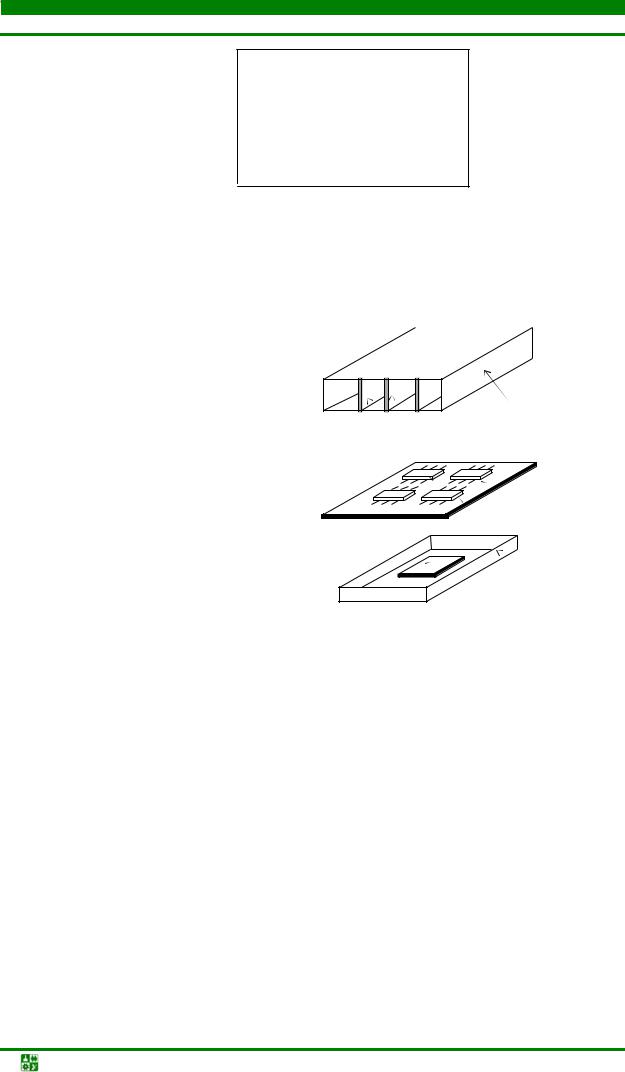
вают входящие в него типовые конструкции предыдущих уровней (см. рис.

4.25).

На рис. 4.25, a приведен

пример

структуры

монтажного

пространства РЭС,

выполненной

на основе печатных

узлов, а на

Блок

рис. 4.25, б - пример

структуры

монтажного пространства

РЭС в

РЭС

микроэлектронном исполнении.

Монтажное

пространство

конструкции

текущего

уровня

Интеграль-

иерархии отражает

ее метриче-

ные схемы

ские и

топологические свойства.

Микросборка

Гибридно-

Метрические свойства –

это га-

баритные размеры зоны

монта-

инте-

жа, допустимая

ширина

про-

гральный

водников и зазора между ними,

Рис.4.25. Примеры монтажных пространств

координаты

размеры

внешних монтажных

площадок,

шаг установки

и размеры

модулей, координаты и размеры полей их контак-

тов и т. п. Топологические свойства – это число слоёв многослойной ПП и

переходов со слоя на слой, наличие замкнутых областей, запрещённых для

проведения соединений, например: вырезы в ПП, наличие тепловых шин для

установки микросхем и микросборок, запрет проведения трассы между вы-

водами микросхем, ограничение на взаимное расположение соединений в

монтажной области и на количество монтажных проводов, подводимых к од-

ному выводу и т. п.

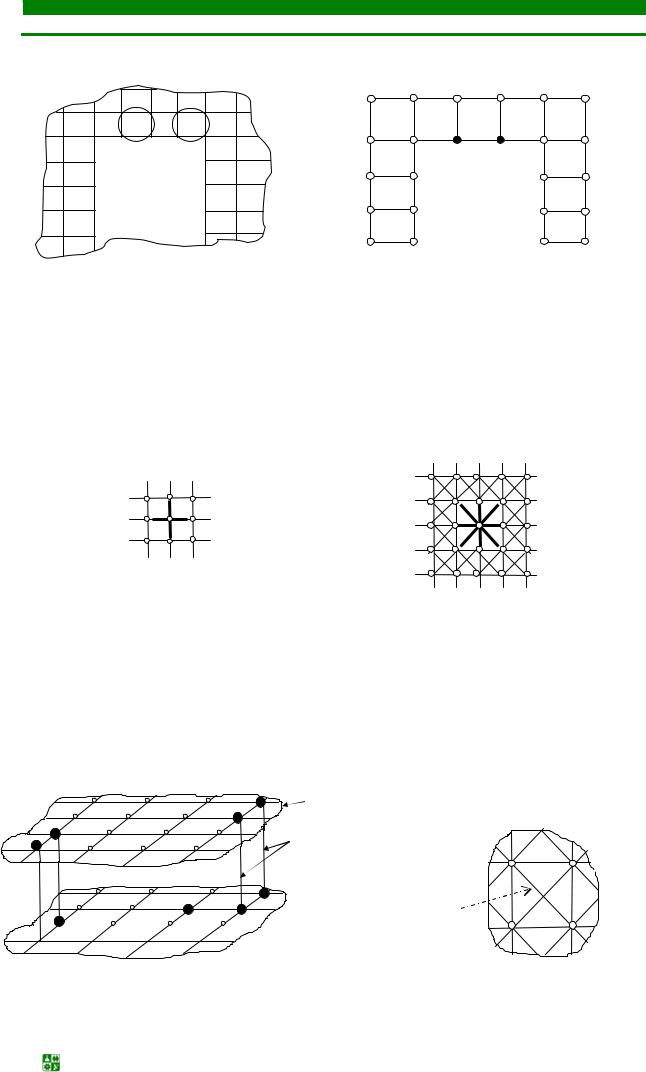
В качестве ММ [13] монтажного пространства, как правило, используют неориентированный граф (граф решётки) Gr. Плоскость монтажа разбивают на элементарные площадки, стороны которых равны шагу проложения проводника по соответствующему направлению (для печатного монтажа элементарная площадка – квадрат). Каждой площадке ставят в соответствие вершину графа решётки (см. рис. 4.26).

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-113-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.6.Математические модели монтажного пространства

Вырез

Рис. 4.26. Фрагмент печатной платы (а) и её граф Gr (б)

Две вершины соединяются ребром, если между соответствующими элементарными площадками можно провести соединение с учетом метрических и топологических параметров типовых конструкций, устанавливаемых в данном монтажном пространстве. В зависимости от направлений, прокладываемых для проводника, каждой вершине графа инциденты могут быть 4

или 8 ребер (рис. 4.27, рис. 4.28).

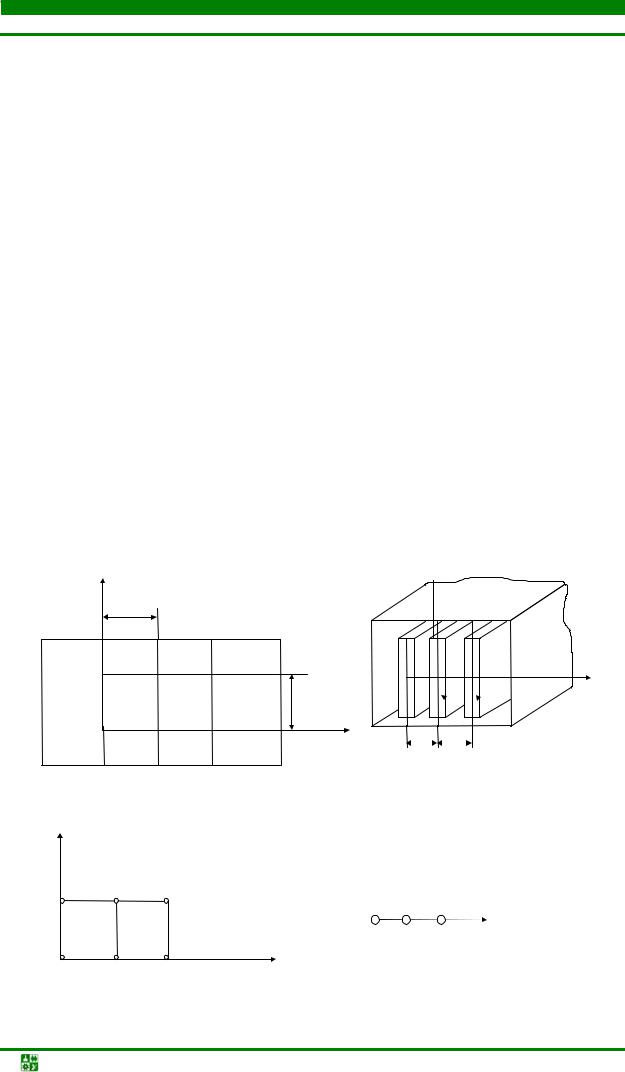
	Рис. 4.27. Разрешенное направление	Рис. 4.28. Разрешенное направление
	прокладки трасс под 90°
		прокладки трасс под 45°

В качестве модели монтажного пространства многослойной ПП может использоваться граф решетки [13], представленный на рис. 4.29. При этом распределение слоев в многослойной ПП может быть следующее: 1-й слой – электрические соединения слаботочных цепей; 2-й слой – электрические соединения малоточных цепей; 3-й слой – разводка цепей питания; 4-й слой – экранирующий слой и т. д.

Слой “n”

Межслойные переходы (вертикальные ребра)

dij

Слой “n+1”

Рис. 4.29. Модель монтажного	Рис. 4.30. Пример полного
пространства многослойной ПП	Рис. 4.30. Пример полного
пространства многослойной ПП	подграфа
	подграфа

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие		-114-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.6.Математические модели монтажного пространства

Для соединений, выполняемых монтажным проводом в любом направлении, вершины графа решетки сопоставляют выводам конструктивного элемента, например, разъема, соединительной платы и т.п. Возможные варианты соединений представляются полным графом, построенным на этих вершинах (рис. 4.30). При таких соединениях необходимо учитывать ограничения на число проводников, подводимых к одному контакту. Расстояние между i-м и j-м узлами графа Gr (см. рис. 4.30) может быть вычислено, в общем случае, следующим образом

dij = ( |Si - Sj|k + |ti - tj|k )h,

где dij – расстояние между вершинами графа (i-м и j-м узлами); S и t – направления вдоль осей x, y; m – число узлов решетки графа; i,j = 1, m;

{k= (2; 1) h =(0,5;1)}.

В ортогональной метрике k=h=1 и, следовательно: dij = |Si - Sj|+ |ti - tj|.

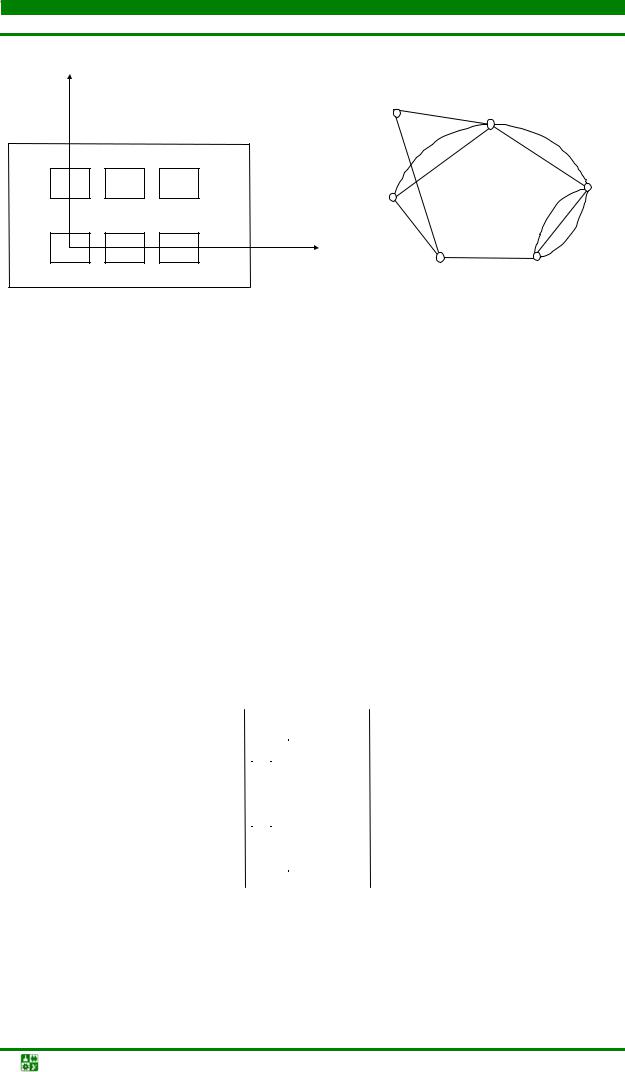
При решении задач размещения, в случаях регулярного монтажного пространства, в качестве модели поля размещения может использоваться граф решетки, вершины которого моделируют установочные позиции элементов предыдущего уровня конструктивной иерархии. На рис. 4.31, рис. 4.32 приведены примеры конструкций РЭС, а на рис. 4.33, рис. 4.34 – модели их монтажных пространств (полей размещения).

В процессе размещения элементов в монтажном пространстве часто

	l
1	2	3
			g
4	5	6	g
4	5	6

Рис. 4.31. Печатная плата с МСБ (l=g)

1	2	3
4	5	6	t
			t

Рис. 4.33. Граф решетки для 6-ти посадочные мест на плате

1 2 3

t	ι1	ι2	ПУ

Рис. 4.32. Блок РЭС

1	2	3	t
			t

Рис. 4.34. Граф решетки для 3-х посадочных мест

в блоке

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-115-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.6.Математические модели монтажного пространства

x6 x1

м1	м2	м3
		x5	x2
		x5
м4	м5	м6
		x4	x3
		t

Рис. 4.36. Графсхема

cоединений модулей м1÷м6

Рис.4.35. Печатная плата с микросхемами

возникает задача расчета суммарной длины соединений между элементами. Для этого можно использовать подход, основанный на применении матриц смежности S, матрицы расстояний Dr и матрицы геометрии Dϒ [13]. Рас-

смотрим такой подход на примере конструкции печатной платы с шестью микросхемами (модулями), имеющими однотипные корпуса (рис. 4.35).

1. Примем в качестве модели схемы соединений неориентированный мультиграф (рис. 4.36), а моделью монтажного пространства платы – граф решетки Gr (рис. 4.33). Вершинам графа сопоставляются модули M1÷M6.

2. Для графа решетки G, отображенного в решетке Gr (вершины графа G в узлах решетки Gr), строится матрица расстояний Dr, элементы которой рассчитываются по формуле

Drij = |Si - Sj|+ |ti – tj |.

Если шаги установки элементов по осям S и t равны, то расстояние между соседними узлами решетки Gr принимается равным 1. С учетом этого матрица Dr будет иметь следующий вид:

		2	3	4		5
	1	2	3	4		5	6
	0	1	2		1	2	3
Dr =	1	0	1		2	1	2
Dr =	2	1	0		3	2	1
	2	1	0		3	2	1
	1	2	3		0	1	2
	2	1	2		1	0	1
		2	1.		2	1
	3	2	1.		2	1	0

3. Определяются длины ребер графа G, отображенного в решетку Gr. Она определяется как полусумма элементов матрицы Dr. Для получения матрицы Dγ, нужно выполнить поэлементное умножение матрицы Dr и матрицы смежности S графа G.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-116-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.6.Математические модели монтажного пространства


	1	2		3		4		5		6			1	2	3		4		5		6
	0		2		0		0		2				0	2		0		0		4
	0		2		0		0		2	1			0	2		0		0		4	3
			0		3		0		0					0		3		0		0
S =	2		0		3		0		0	0		Dγ =	2	0		3		0		0	0
											;
	0		3		0		1		0	0	;		0	3		0		3		0	0
	0		3		0		1		0	0			0	3		0		3		0	0
	0		0
	0		0		1		0		1	1			0	0		3		0		1	2
	2		0		0		1		0				4	0		0		1		0
	2		0		0		1		0	0			4	0		0		1		0	0
			0		0		1		0					0		0		2		0
	1		0		0		1		0	0			3	0		0		2		0	0

Сучетом изложенного суммарная длина L(a) ребер графа G равна 18.

Впроцессе решения задач размещения разногабаритных элементов на

ППмогут применяться позиционные графы Gx и Gy [42]. В этом случае схема размещения элементов (или фрагментов схемы) представляется в виде модели плотной укладки, пример которой приведен на рис. 4.37. В такой модели элементы представляются прямоугольниками, соприкасающимися своими границами.

									7
		P2					P9		6
5		P2					P8		6

		P1		P4					4



						P5		P7	3
				P3				P7	3

									2
1								P6	2
1								P6

	1		2		3		4		5

Рис. 4.37. Модель плотной укладки

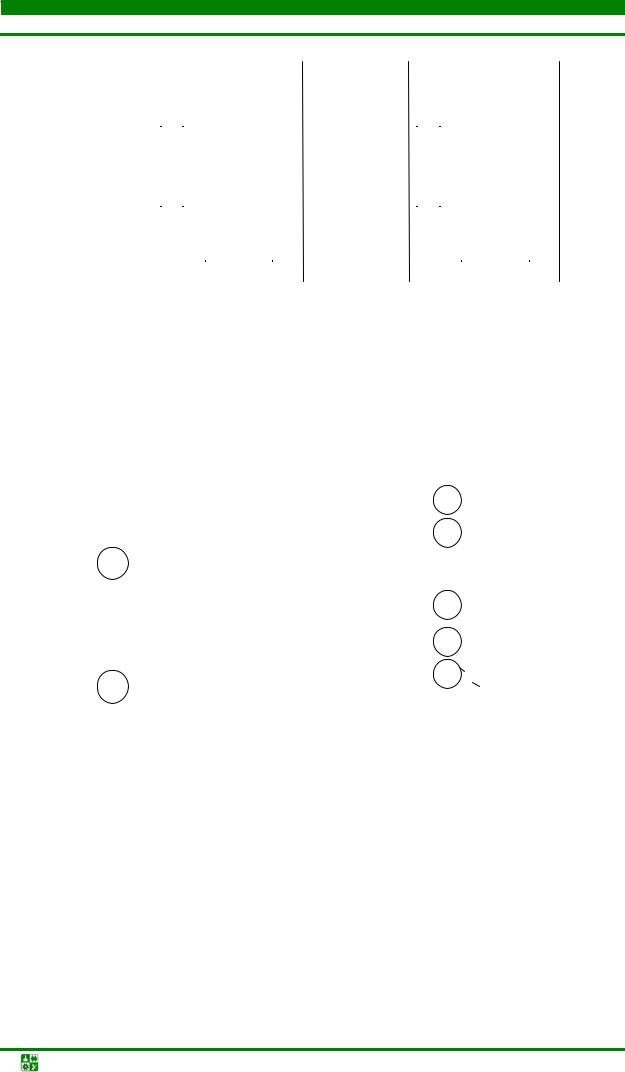
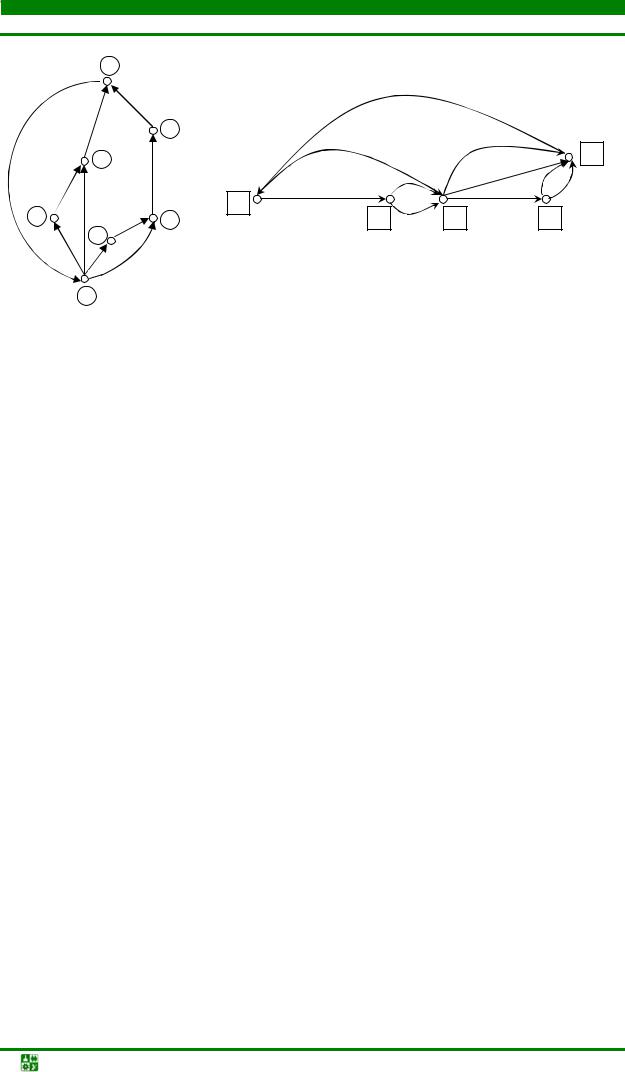
Вершинами графа Gx = (X, U) являются горизонтальные уровни, пронумерованные по возрастанию координаты уровня. Ребро pi = (xi , xk ) имеется в множестве U тогда и только тогда, когда xi и xk – уровни расположения сторон некоторого прямоугольника. Аналогичным образом определяют граф Gy = (X, U), с той лишь разницей, что горизонтальный уровень заменяется вертикальным. На рис. 4.38 приведен пример графов Gx и Gy для схемы укладки, представленной на рис. 4.37. На указанных рисунках горизонтальный уровень отмечен кругом, а вертикальный – квадратом.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-117-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.6.Математические модели монтажного пространства

	7
		Р9			Р0
					Р0
Р0	Р2	6					Р9
Р0							Р9		5
	5			Р2					5
	5	Р8		Р2			Р8
Р4		Р8					Р8	Р7	Р6
Р4	Р1 Р7	1	Р1		Р4		Р5	Р7	Р6
3	Р1 Р7	4	Р1	2	Р3	3	Р5		4
	2				Р3
Р3	2
Р3	Р6	Р5
	Р6	Р5
	1				б
					б

Рис.4.38. Позиционные графы для плотной укладки: а – вертикальный граф; б – горизонтальный граф

Позиционные графы являются ориентированными и обладают следующими свойствами:

1.Графы имеют вершину-исток с наименьшим и вершину-сток с наибольшим номером; для вершины-истока все ребра, кроме одного, являются исходящими, а для вершины-стока все ребра кроме одного, являются входящими.

2.Промежуточные ребра графов, не инцидентные истоку или стоку, направлены от вершины с меньшим номером к вершине с большим номером.

3.Графы являются планарными, т. е. могут быть изображены без пересечения ребер.

4.Ребра графа Gx(Gy) имеют направление вверх (вправо), т. е. в сторону возрастания номера вершины, за исключением ребра для заключающего все элементы прямоугольника p0, противоположно ориентированного.

При построении моделей межфрагментальных соединений используют модели многополюсников [42].

Математической моделью многополюсника является циклическая замкнутая последовательность (циклическая структура) А=(а1, а2,,…, ап).

Циклическая замкнутость означает, что последовательности А1=(ап, а1,…, ап-1), А2=(ап-1 , ап,,…, ап-2),…, отличающиеся от А циклическим сдвигом ее компнентов на 1,2,… позиций вправо, описывают один и тот же многополюсник.

В некоторых задачах многополюсник А может играть роль обычной последовательности. Элементы а1, а2,,…, ап в зависимости от решаемой задачи могут быть идентификаторами позиций выводов фрагментов либо цепей, им инцидентных.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-118-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.6.Математические модели монтажного пространства

Применение некоторых операций последовательности А позволяет организовать соединение одноименных выводов, в чем и состоит задача трассировки, если учитывать только ее топологические характеристики.

Рассмотрим модель трассировки соединений применительно к следующей задаче [42].

Задан многополюсник А1=(а1, а2,…, ап). Элементы а1, а2,,…, ап представляют собой номера цепей, которым инцидентны соответствующие выводы. Во внешней области многополюсника известно расположение соединений объединяющих одноименные выводы. Требуется математически описать эти соединения.

Для числовой последовательности B=(b1, b2,,…,bm) введем три типа операций:

1.Объединение fi, заменяющее последовательность Bi B одноименных элементов начинающихся с номера i одним элементом с тем же названием.

2.Исключение θi, позволяющие удалить из последовательности B эле-

мент bi.

3. Транспозиция φi, в результате которой меняются местами элементы

bi и bi+1.

Интерпретировать представленные выше операции можно следующим образом: соединение смежных выводов одной цепи, удаление некоторой завершенной цепи из рассмотрения, организация пересечения двух различных цепей.

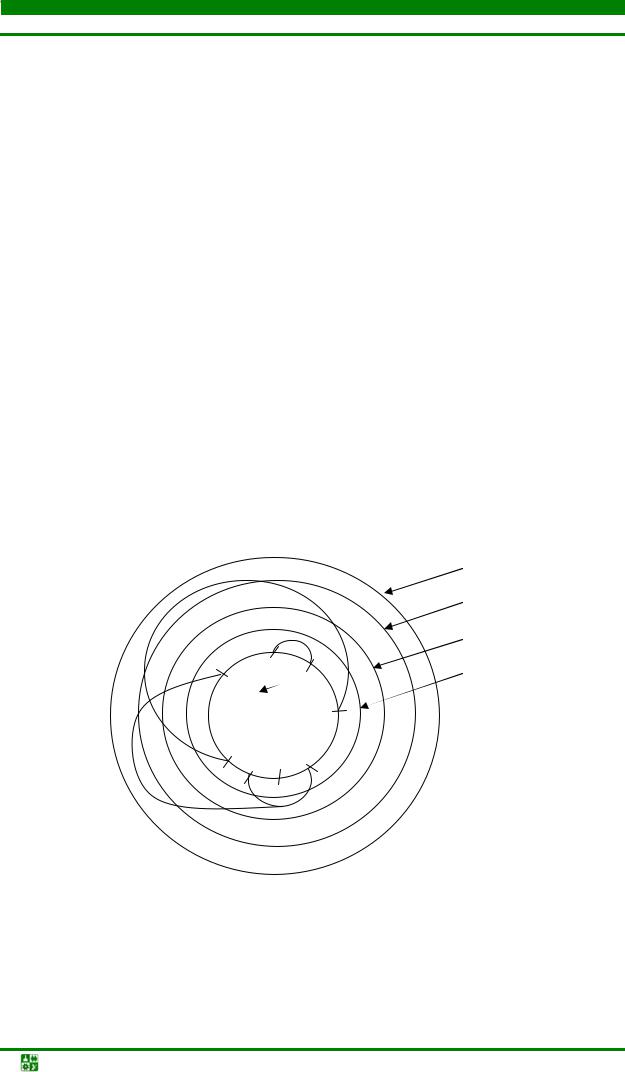
На рис. 4.39 представлена схема соединений одноименных полюсов многополюсника.

				3			А4=
				3			А3
						3	А3
					1	3	А2
					1		А2
3	2	2	2	1	1	3	А1
3	2		2			3
2 3						3
2 3
		3	3 2	4	2
	2		2			2
	2		2
			2

Рис. 4.39. Схема соединений одноименных полюсов многополюсника: А1–А4 – многополюсники

Одна из возможных моделей этой схемы имеет следующее описание:

А=(1, 2, 3, 2, 4, 2, 3, 1); θ5А=1, 2, 3, 2, 2, 3, 1); А1=f7(θ5А)=(2, 3, 2, 2, 3, 1);

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-119-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.6.Математические модели монтажного пространства

θ6А1=(2, 3, 2, 2, 3); А2=f3(θ6А1)=(2, 3, 2, 3); А3=ϕ1А2=(3, 2, 2, 3);

f2А3=(3, 2, 3); f3(f2А3)=(2, 3); θ1(f3(f2А3))=(3); А4=θ1(θ1(f3(f2 А3)))= .

Таким образом, модель трассировки можно представить в виде списка последовательностей А=А0, А1,..., Ак= , где Аi можно представить как последовательные фазы трассировки, причем Аi+1=ΨiАi, а Ψi – некоторая суперпозиция операторов объединения, исключения и транспозиции; А0 – начальная фаза, совпадающая с описанием многополюсника; Ак= – заключительная фаза, когда трассировка всех цепей завершена.

При иерархическом проектировании важно обеспечить трассировку с заданными граничными условиями B. В общем случае модель трассировки – это последовательность операций объединения, исключения, транспозиции, для которой ΨА=B. Если B= , то граничные условия отсутствуют.

4.7. Алгоритмыкомпоновки

Общая задача компоновки была дана в параграфе 4.4. Для более точной постановки задачи рассмотрим основные положения задач компоновки. В процессе решения задачи компоновки, в качестве критериев оптимизации, обычно используют следующие критерии [13]:

1. Минимум суммарного числа модулей, необходимых для реализации схемы (критерий связан с избыточностью реализации):

Ni = ∑xi, j , j I

где xi,j – число модулей j-го типа i-го уровня, полученное в результате компоновки схемы.

2. Минимум числа типов используемых (скомпонованных) модулей или максимум коэффициента их повторяемости. При этом коэффициент повторяемости вычисляется как

kповт =1− mn , Ni−1

где n – число типов модулей; m – число элементов (i-1)-го уровня в модуле (типовой конструкции); Ni-1 – общее количество элементов (i-1)-го уровня в схеме.

3. Минимальная избыточность в реализации:

mi = ∑ mi,k , k=1

где ∆mi,k – число неиспользованных элементов в каждом модуле i-го уровня. 4. Минимум межмодульных соединений:

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-120-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.7.Алгоритмы компоновки

Алгоритмы компоновки

конструктивных узлов

типовых конструкций (моду-

лей)

Модули с

Модули

Матема-

Последо-

Параллель-

Итера-

несвязан-

со свя-

тические

вательные

но-последо-

ционные

ными

занны-

модели

алгоритмы

вательные

алгорит-

элементами

ми

алгоритмы

мы

элемен-

тами

Методы	Ком-	Алгорит-
Методы	Ком-	Алгорит-	Алгорит-	Алго-
целочис-	бина-	мы пар-	мы груп-	ритмы
ленного	тор-	ных пере-	повых	покры-
програм-	ные	становок	переста-	тия
мирова-	мето-		новок	схем
ния	ды

Последо-		После-
ватель-		дова-
ные алго-		тельные
ритмы		эвристи-
		ческие
		процеду-

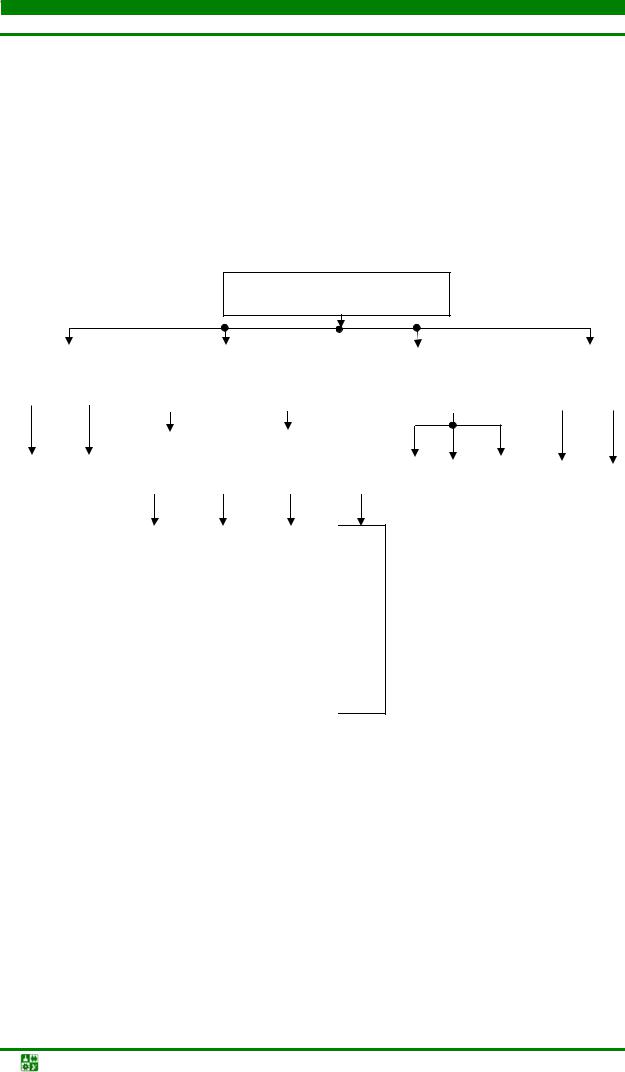
Рис. 4.40. Классификация алгоритмов компоновки

1 Ni

Ri = 2 ∑Ri,k , k=1

где Ri,k – число внешних связей каждого модуля i-го уровня или минимум суммарного числа внешних выводов всех модулей Si:

Si = ∑Si,k , k=1

где Si,k – число внешних выводов каждого модуля i-го уровня.

Критерии 1–3 напрямую связаны с конструктивными параметрами РЭС и показателем стоимости. Критерий 4 ведет к повышению надежности конструктивной реализации схемы за счет сокращения числа разъемных соединений, уменьшению помех и задержек сигналов благодаря снижению суммарной длины соединений. Использование того или иного критерия зависит как от вида задачи компоновки (разрезание или покрытие), так и от уровня иерархии. Например, при покрытии схемы электрической функциональной заданным набором ИС критерий 2 не является определяющим, в то время как при покрытии схемы устройства некоторым набором ТЭЗ этот критерий имеет важное значение.

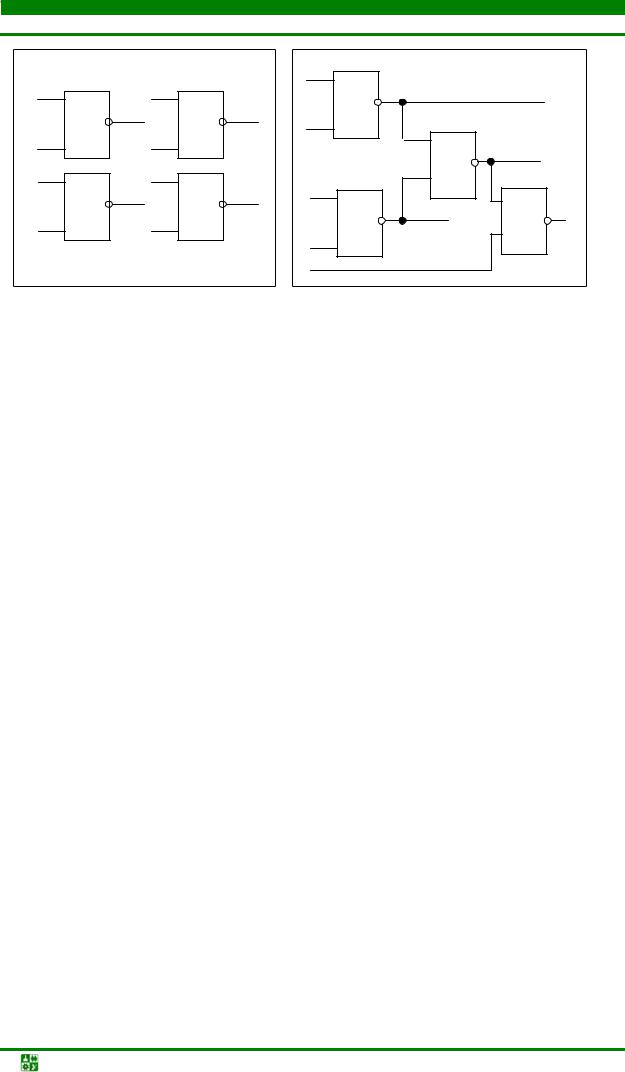
Классификация алгоритмов компоновки [43], представленная в виде схемы? приведена на рис. 4.40. На рис. 4.41 приведены примеры модулей, на которые ориентируются алгоритмы компоновки типовых конструкций.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-121-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.7.Алгоритмы компоновки

				3
1	&	9	&	1			12
1		9					12
				4
2	3	10	8	4
2		10			1		11
					1

4	&	1	&	5
	&		&
	6		1				1
	6		1	1			1
5		1				10	13
5		1		5		10
				5
			а	2			б
			а				б

Рис. 4.41. Модули, состоящие из несвязанных (а) и связанных (б) элементов

Рассмотрим в общих чертах несколько наиболее часто используемых в практике типовых алгоритмов компоновки [13, 42]. Перед рассмотрением алгоритмов введем следующие обозначения [42]: Lα – число соединений между

элементами блока (модуля) Bα ; L(i,j) – число соединений между парами элементов еi и еj (ei Bα, ej Bβ); LB – общее число внутриблочных (внутримодульных) связей; LM – общее число межблочных (межмодульных связей); LС – общее число связей схемы.

Обычно предполагается, что в качестве исходной информации задается матрица взвешенных связей R. Ввиду симметрии матрицы (rij=rji) можно использовать только ее часть, лежащую над главной диагональю. С учетом введенных ранее обозначений запишем:

n	n		n	nβ
α−1	α		α
Lα = ∑ ∑ rij ;		L(α,β ) = ∑ ∑Nij ;
i=1 j=i+1			i=1	j=1
l		l−1	l
LB = ∑Lα ; LM = ∑ ∑ L(α, β );
α=1		α=1	β=α+1
LC = LB + LM ,

где nα, nβ – количество элементов в блоках Bα и Bβ; l – число блоков (модулей), в которые компонуется схема.

Используя введенные обозначения уточним постановку задачи компо-

новки [42].

Постановка задачи. Распределить элементы e1, e2,..., en множества Е по блокам В1, В2,..., Вl, т. е. представить множество Е в виде разбиения

E = Bα

α=1

, Bα∩Bβ= , (α≠β) при ограничениях

Bα =nα, α=1,2,..., l, ∑nα = n .

α=1

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-122-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.7.Алгоритмы компоновки

4.7.1. Алгоритмыпарныхперестановок (минимизациячисламежблочныхсоединений)

Для решения задачи введем величину LM(x, y) – приращение числа межмодульных соединений при перестановке местами элементов x и y:

			LM (x, y) =[Lвншx	j	− Lвнx	] +[Lвншy	− Lвнy ] − 2rxy ,
	Lвншx			j	i	i	j
где	Lвншx	j	(Lвншy ) – число		внешних соединений элемента lx и ly; rxy–
		j	i

элемент матрицы смежности R.

Если Dx = Lвншx j − Lвнxi – разность числа внешних и внутренних соединений элемента lх, а Dy = Lвншyi − Lвнy j – разность числа внешних и внутренних соединений элемента ly, то

LM(x,y) = Dx + Dy – 2rxy.

Данное выражение будет рассматриваться в дальнейшем в качестве функции-критерия.

Стратегия рассматриваемого алгоритма заключается в следующем [43]:

1.В некотором блоке (модуле) Вi выбирается элемент ех.

2.Осуществляется попытка обмена этого элемента последовательно со всеми элементами, не принадлежащими данному блоку (модулю).

3. Рассчитывается значение приращения функции-критерия F ( F=F0 –F1, где F1 – полученное значение F при текущей перестановке пары

элементов). Если F >0, то обмен осуществляется.

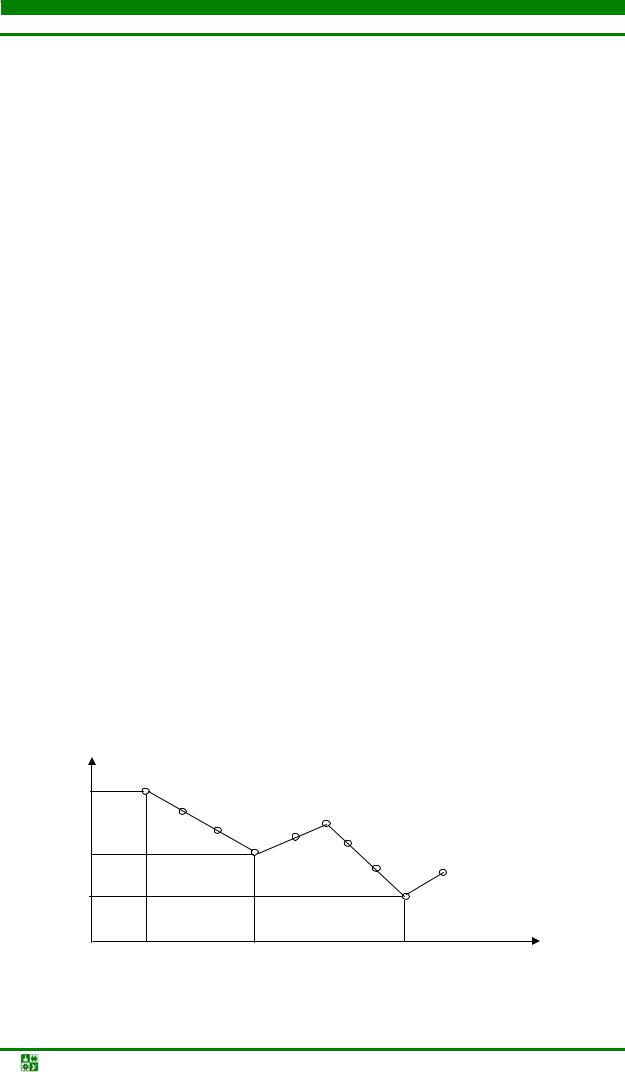
4. Процесс повторяется до тех пор, пока существуют перестановки, уменьшающие значение F. В результате получают последовательность вариантов компоновки k0, k1,… ,kz, которым соответствуют монотонно убывающая последовательность значений целевой функции-критерия F0>F1>F2>…>Fz. Таким образом, данный итерационный процесс может привести к локальному оптимуму [13] (Fm, Km), как это показано на рис. 4.42 (пройти локальный оптимуму позволяет метод групповых перестановок).

Fmin

Рис. 4.42. Процесс изменения целевой функции-критерия F

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-123-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.7.Алгоритмы компоновки

Начало

q=1, q*,1

2 i=1

j=(i+1), γ,1

Выбор пары модулей

Bα и Bβ

5 Расчет характеристик D

Сортировка D

Вычисление

Корректировкахарактеристик D

				9
					Обмен:
			1
8

					x s→ Bβ
	LMmax >0				x s→ Bβ
	LMmax >0				y s→ Bα
		0			y s→ Bα

i=i+1

0 11

i=γ-1

Рис. 4.43. Блок - схема алгоритма парных перестановок: γ – количество блоков (модулей)

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-124-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.7.Алгоритмы компоновки

Пусть, например, схема устройства задана матрицей Rn,n и известен некоторый вариант разбиения схемы на l модулей. В результате возможной

реализации алгоритма [43] выбираются модули Вα и Вβ		и расчет		LM(x, y)
производят в следующей последовательности. Сначала находят Dz для всех
еz Bα или Вβ и выбирается пара ех1 Bα, еy1 Bβ, для которой			LM(x1, y1) мак-
симально и больше нуля. Производят обмен. Зафиксировав обмен, из остав-
шихся элементов получают пару ex	и e y , для которой	LM(x2, y2) > 0. Про-
2	2			LM(x,y) >
цесс заканчивают, когда на очередном шаге нет ни одной пары с
0.			LM(x,y) может
С целью уменьшения времени вычислений D при расчете

использоваться свойство неизменности некоторых значений D, рассчитанных на предыдущем шаге. С этой целью можно предварительно упорядочить

характеристики			по	уменьшению				D		и первыми	кандидатами для
обмена		выбирать			элементы				с	начала	последовательности
Dx	> Dx	> Dx	> Dy		> Dy	2	> Dy	k	.	Алгоритм, реализующий данный
1	2	k		1		2		k

подход [43], приведен на рис. 4.43.

4.7.2. Алгоритмгрупповыхперестановок

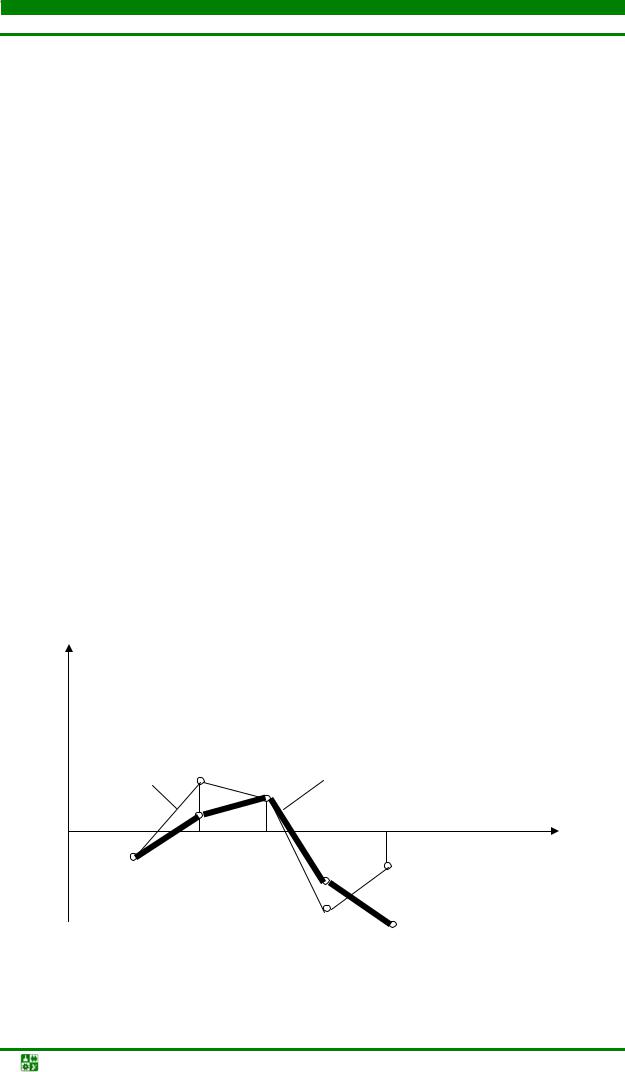
Как уже отмечалось выше метод групповых перестановок позволяет пройти локальный оптимум. Рассмотрим один из способов определения группы [13]. Для всех пар элементов ai A и bi B определяют приращение функции-критерия F. Выбирают пару элементов с максимальным F, обозначают их a1 и b1 и временно осуществляют их перестановку (значение F может быть: F<0; F =0; F >0 ). Процесс повторяют k раз до тех пор, пока все элементы подмножества А и В не поменяются местами. Затем строится зависимость F от шага обмена k, как это показано на рис. 4.44.

∆F P

∆F Р

1	2	3	4	5

Рис. 4.44. Изменение приращения ∆F и их суммы P

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-125-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.7.Алгоритмы компоновки

По полученной кривой определяют шаг обмена k*, при котором

p = ∑ Ft > 0 и максимальна (Т=1,2, …, k). После этого выполняют обмен t=1

группы а1, а2,..., ак из узла А на группу b1, b2,..., bк из узла В.

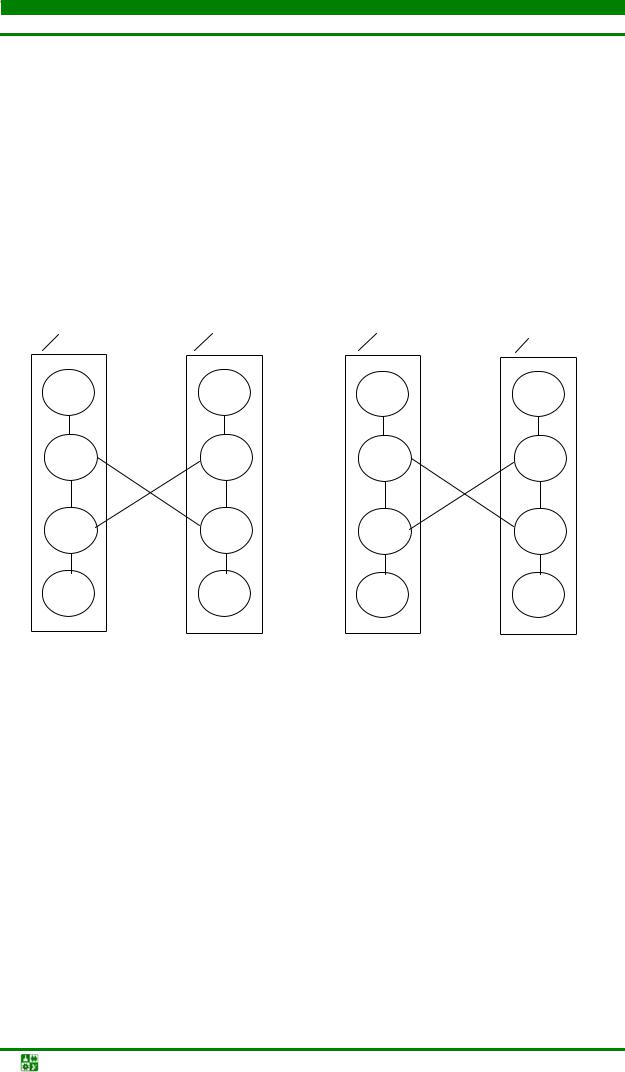
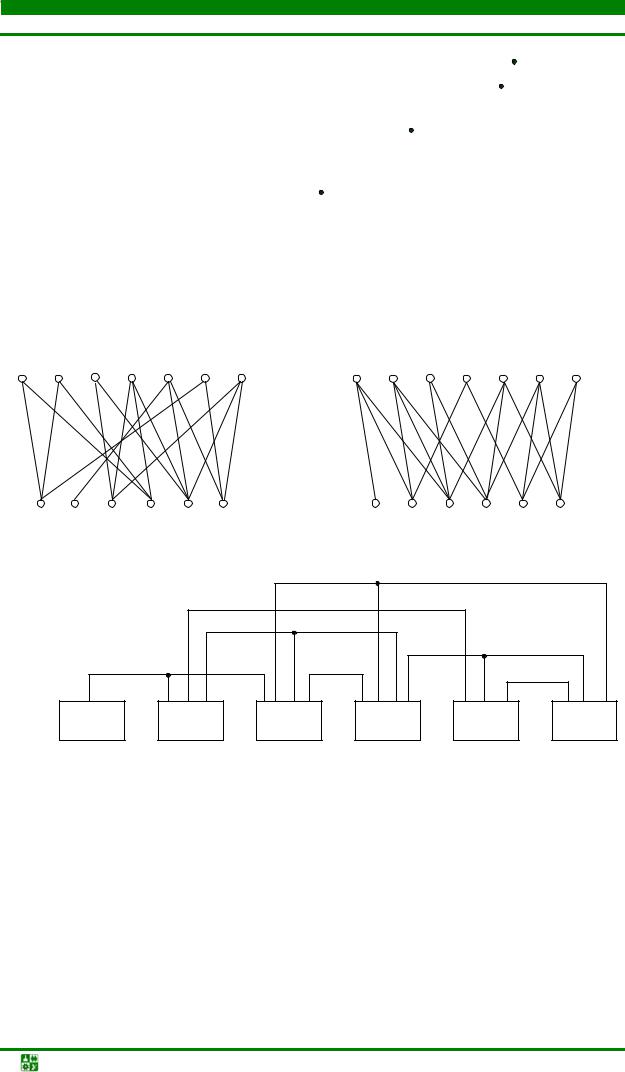
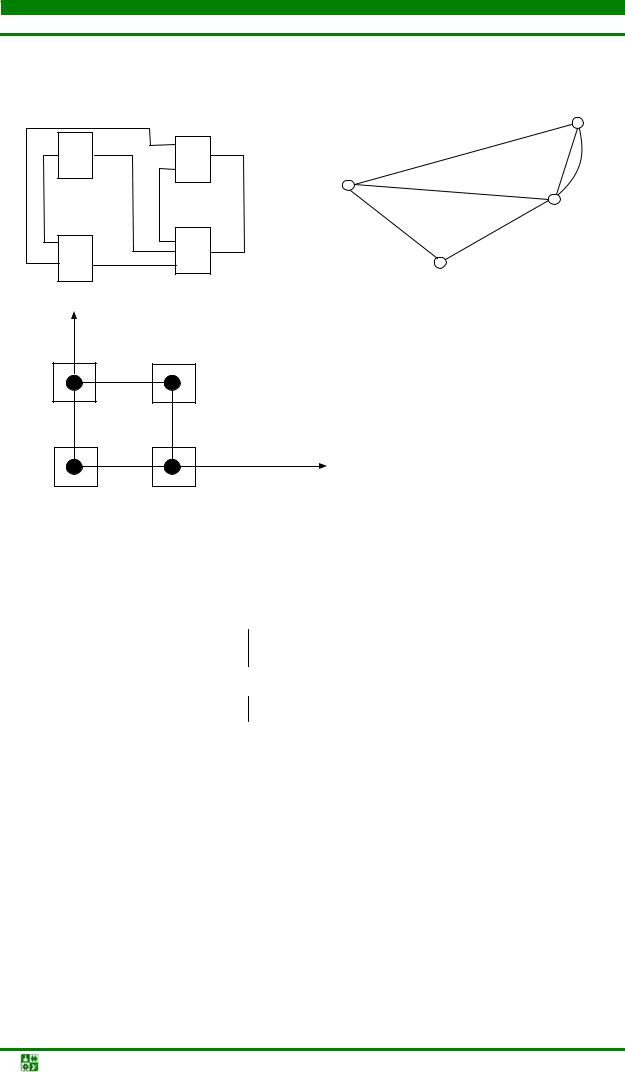
Пример группового обмена, улучшающего критерий межэлементных связей [13], приведен на рис. 4.45, где цифрами около линии, соединяющей элементы, указано число связей между ними. Обмен любой пары элементов не уменьшает число межмодульных соединений. Перенос же элементов е1 и е2 в модуль 2, а элементов е5 и е6 в модуль 1 приводит к уменьшению межузловых связей с 6 до 2.

Модуль 1

Модуль 2

Модуль 1

Модуль 2

е1		е5		е5		е1
6		6	6			6
е2	3	е6		е6	1	1 1 е2
1		1	3			3
е3	3	е7		е3		е7
е3		е7		е3		е7
6		6	6			6
е4		е8	а	е4		е8
			а			б

Рис. 4.45. Пример группового обмена элементами: исходная компоновка (а) и результат обмена (б)

В заключение отметим, что итерационные алгоритмы компоновки обеспечивают лучшее качество решения задачи, чем последовательные, однако требуют больших затрат машинного времени. Более детально с алгоритмами компоновки можно ознакомиться в [13, 14, 26, 42, 43].

4.8. Алгоритмыразмещения

Главной целью задачи размещения, как отмечалось в параграфе 4.4, является создание наилучших условий для последующей трассировки. На рис. 4.46 приведен пример размещения элементов и трасс некоторого фрагмента электрической схемы на дискретном поле.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-126-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

		(6)
		(6)				(5)			(7)
						(5)			(7)
									(3)

										(4)

				(2)
			(1)
		е1			е2				е3			е4			е5				е6

Позиции		1			2			3				4				5		6
											а
Начальный вариант размещения											Окончательный вариант размещения
(1)	(2)	(3)	(4)	(5)	(6)		(7)	(5)				(7)	(3)	(6)		(4)	(1)	(2)

е1 е2	е3	е4 е5 е6		е2 е6 е5	е3	е1 е4
			б
		(6)	(4)
		(6)
		(7
						(1)
	(5)			(3)		(2)
						(2)
	е2	е6	е5	е3	е1	е4
Позиции	1	2	3	4	5	6
			в

Рис. 4.46. Пример размещения элементов и трасс некоторого фрагмента электрической схемы на ДРП: а –начальный вариант размещения; б –двудольный граф;

в–окончательный вариант размещения

Впроцессе решения задачи размещения используются следующие основные критерии [13]:

1. Минимум суммарной длины всех соединений или длины самой длинной связи.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-127-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

2.Минимум числа пересечений связей при произвольной их конфигурации.

3.Максимум числа цепей с возможно более простой конфигурацией.

4.Максимально близкое расположение модулей, имеющих наибольшее количество связей между собой.

Наиболее часто используется критерий минимума суммарной длины соединений, так как при его оптимизации косвенно минимизируются длина связей и число их пересечений, снижаются искажения сигналов. В последнее время считают, что критерий 2 является более глубоким при решении ряда задач топологического проектирования микроэлектронных узлов [42].

Алгоритмы размещения

Математические	Конструктивные алго-	Итерационные	Непрерывно-
модели	ритмы начального	алгоритмы	дискретные
	размещения	размещения	методы

Последова-

Параллельно-

тельные ал-

последователь-

Аналитические методы оптимизации

горитмы

ные алгоритмы

Метод ветвей и границ

Алгоритм последовательного размещения по связанности

Матричные алгоритмы размещения

Метод обратного размещения

Метод разбиения

Алгоритм парных перестановок		Алгоритм групповых перестановок		Метод случайного поиска		Метод силовых функций		Метод последовательного сдвига

Рис. 4.47. Классификация алгоритмов размещения

Для N элементов, которые могут быть установлены в M позиций, существует множество A= {al / l=1, L} размещений. При этом L определяется как

[13]:

M!/(M − N)! при M > N
L =	приM = N.
M!

В связи с этим поиск оптимального варианта размещения элементов полным перебором нецелесообразен уже при N= 15 – 20. В дальнейшем бу-

дем полагать, что M=N.

Классификационная схема алгоритмов размещения [43] представлена на рис. 4.47.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-128-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

4.8.1.Последовательныйалгоритмразмещения

Исходными данными для алгоритма являются: матрицы R (матрица взвешенных связей) и матрица расстояний Dr, вектор взвешенных связей элементов с внешними выводами Н, множества индексов размещенных Ik и

неразмещенных Ik элементов множества индексов занятых и свободных

позиций Тk и Tk .

Вектор Н – вектор-столбец взвешенных связей Н={hi / i=1,N} выводов элементов ei с элементом e0 (внешние выводы – разъем). Монтажная область внешних выводов (контактных площадок) обычно размещается на периферии типовой конструкции. Контактные площадки инвариантны, за исключением выводов питания и земли. В связи с этим расстояние от элемента ei до внешних выводов (элемента e0) можно приближенно определить как расстояние от вертикального (горизонтального) ряда, в котором установлен этот элемент, до контактной группы е0 (см. рис. 4.48).

K0		1		1		4	(7)	1		x1	x2	x3		1	1
	е1	2	(1)	2				2		x1	x2	x3
		2		2	е2			2	е3	e0				0	2
4		3	(2)	3	е2			3	е3	e0			H=	0	2
													H=	3	3


		(3)			(4)										4
					(4)		(6)							1



(5)				1							x4
				2	е4	3			e0	а			б		в
				2	е4

Рис. 4.48. Фрагмент схемы (а), мультиграф схемы (б) и вектор H (в)

Правила выбора элементов в процессе размещения можно сформулировать следующим образом:

1.max {ri , jk },

iIk

где jk – номер столбца матрицы R.

m ax

∑ ri , j .

i I

j I

m a x

∑ ri , j

∑

−

ri , j .

i I

j I

Показатель качества позиции при использовании матрицы Dr можно оценить как

Li , f = ∑ ri , j d f , t ( j ) + m f hi ,

j I k

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-129-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

где t(j) Tk – индекс позиции j-го размещенного элемента; mf – номер вертикального ряда, в котором расположен элемент ef.

Для размещения i-го элемента среди незанятых позиций выбирают ту, что обеспечивает

m in
m in
		∑ ri , j d f ,t ( j ) + m f hi .
		∑ ri , j d f ,t ( j ) + m f hi .
f T
	k j I		k
			k

Сформулируем основные этапы алгоритма размещения по мультиграфу схемы:

1. По одному из правил 1–3 определяется индекс ik+1 очередного раз-

max

мещенного элемента. Например: i k + 1 =

∑ ri , j .

i I k j I k

2. Определяют позицию для установки этого элемента:

m in

f k +1

∑ rl j d f ,t ( j ) + m f hl

T k

j I

где l = ik+1.

3. Заносят индекс элемента в массив Ik, индекс позиции – в массив Tk, исключая их из массивов Ik и Tk : Ik = Ik ik +1 , Ik = Ik \ ik +1, Tk =Tk fk +1 ,

Tk =Tk \ fk +1.

4.Выполняется проверка – все ли элементы размещены (Ik≠0). Если «Да», переходят к пункту 1, иначе – к пункту 5.

5.Конец алгоритма.

Рассмотрим пример применения описанного алгоритма. Для примера возьмем фрагмент схемы, представленной на рис. 4.48. В качестве монтажного пространства примем модель, приведенную на рис. 4.49.

	е3			е0
1	2	3	4	5

Позиции

Рис. 4.49. Модель монтажного пространства

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-130-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

Для модели монтажного пространства построим матрицу Dr

		1	2	3	4	5
	1
	1	0	1	2	3	4
	2
Dr=	2	1	0	1	2	3	.
	3
		2	1	0	1	2
		2	1	0	1	2
	4	3	2	1	0	1
	5
	5	4	3	2	1	0

Допустим также, что элемент е3 является уже размещенным, а элемент е0 закреплен в 5-й позиции. При принятых допущениях множества исходных индексов будут иметь следующий вид: IK={3}; TK={2, 5}; Ik ={1, 2, 4};

Tk ={1, 3, 4}.

Матрица R будет иметь вид:

	1	2	3	4

1	0	2	0	2

2	2	0	2	0
Dr=
Dr=	0	2	0	2
3	0	2	0	2

4	2	0	1	0

Выполним алгоритм по шагам.

1 - й шаг. Выбираем критерий


ii +1
ii +1	= l = max			∑ ri, j .
			j
		k	j		I	k
	i I	k				k
	i I

Определяем элемент для размещения исходя из выбранного критерия.

1. i=1: ∑r1,3 = 0.

j =3

2. i=2: ∑r2,3 = 2.

j =3

3. i=4: ∑r4,3 =1.

j =3

Следовательно ik +1 = max{0, 2, 1} = 2 .

2 - й шаг. Определим позицию для установки второго выбранного элемента ik +1 = l = 2 .

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-131-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

Изменяем f: f=1, 3, 4.

1. f=1: ∑ r2,3 d1,2 + 0 = 2 1 = 2 .

j=3

2.f=3: ∑r2,3 d3,2 +0 =2 1=2.

j=3

3. f=4: ∑r2,3 d4,2 +0 =2 2 =4. j=3

rk +1 = min{2, 2, 4} = 2 и, следовательно, f=1.

3 - й шаг. Преобразуем индексы: JK = JK ik +1 ={3, 2};

JK = JK \ ik+1={1, 4}; TK ={2, 5, 1}; TK ={3, 4}.

и т. д.

4.8.2. Итерационныйалгоритмулучшенияначальногоразмещения

Алгоритмы данной группы [13] ориентированы на то, что для улучшения некоторого начального размещения элементов (модулей) меняются местами те элементы, перестановка которых приводит к оптимизации критерия качества. Процесс заканчивают, если не существует перестановок, улучшающих критерий качества, или когда разность значения критерия для двух соседних итераций будет меньше некоторого заданного значения.

Ввиду того что реализация итерационных алгоритмов связана с большим объемом вычислений, практическое применение находят в основном алгоритмы, использующие парные и упорядоченные перестановки.

В качестве критерия возьмем критерий минимума суммарной длины соединений L(a).

Соединения элементов схемы определены матрицей S, расстояние между установленными позициями – матрицей Dr. Имеется некоторое начальное размещение элементов. Элементы матрицы S должны располагаться в соответствии с порядковыми номерами (индексами) позиций их установки. Например, для начального размещения четырех элементов (см. рис. 4.50) матрицы Dr и S будут иметь следующий вид:

		1 2 3 4						e1		e1 e3	e2	e4
	1	0	1	1	2				0	1	0	1
Dr=	2	1	0	2	1	,	S=	е3 1		0	1	1	.
	3							eе23	0	1	0	2
		1	2	0	1
	4	2	1	1	0			e4	1	1	2	0

В матрице S первая строка характеризует связанность элемента е1 с

элементами е3, е2, е4, вторая строка – элемента е3 с элементами е1, е2,.	е4, тре-

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие	-132-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

тья строка – элемента е2 с элементами е1, е4, е3 и строка четыре – элемента е4 с элементами е1, е3, е2.

(3)				X2
				X2
e1			e2
(1)	(2)	(5)		X3
(1)	(2)	(5)	(4)	X4
				X4
e3	(6)		e4	б
e3	(6)		а
			а
				X1
y
e1			e3
1			2	Рис. 4.50. Пример схемы соединений
				Рис. 4.50. Пример схемы соединений

вэлементов (а), мультиграф схемы (б)

ивариант размещения элементов (в)

e2 e4

3 4

Переставляя элементы ei и ej, необходимо в матрице S поменять местами соответствующие им строки и столбцы. Например, переставив элементы e1 и e3 местами, получим следующую матрицу S:

	е3	е3	e1	e2	e4
	е3	0	1	1	1
S=	е1	1	0	0	1
	e3	1	0	0	2
	2
	e4	1	1	2	0

Аналогичный результат для оценки L(a) путем перемножения матриц S и Dr, можно получить, сохраняя неизменной матрицу S. При этом элементы матрицы Dr располагают в соответствии с индексами установленных элементов. После изменения позиций элементов еi и еj корректируют матрицу Dr посредством перестановки в ней строк и столбцов, определяющих расстояние переставляемых элементов до остальных.

Рассмотрим процесс получения выражения для подсчета приращения функционала L = Lk−1 −Lk в общем виде.

Пусть элементы е1–е3 установлены в позиции 1–4. Для данного размещения суммарная взвешенная длина соединений будет равна.

Lk-1=s12d12 +s13d13+s14d14+s23d23+s24d24+s34d34.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-133-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

Поменяем местами элементы ei и ej. Тогда в матрице D переставим 1-ю и 3-ю строки и столбцы. В результате получим

		3	2	1	4
	3		d32	d31	d34
	3	0	d32	d31	d34
Dr=	2	d24	0	d21	d24
Dr=	1	d31	d24	0	d14
	1	d31	d24	0	d14
	4	d43	d42	d41	0

Для полученного варианта размещения функция качества будет иметь вид

Lk=s12d32+s13d31+s14d34+s23d21+s24d24+s34d14

Приращение функции качества

L = s12(d12 − d32) + s14(d14 − d34) + s23(d23 − d21) + s34(d34 − d14) .

После несложных преобразований получим

L = (s12 − s32 )(d12 − d32 ) + (s14 − s34 )(d14 − d34 )

В общем виде

L =∑(si,n −s j,n)(di,n −d j,n), n ≠i, j ,

(4.1)

где n – индекс элемента, не участвующего в перестановке.

В итерационных алгоритмах парных перестановок используют различные способы упорядочивания переборов для уменьшения числа возможных перестановок. Один из таких способов заключается в следующем: для данного размещения определяют скалярное произведение – суммарную длину связей Li каждого элемента с остальными как соответствующих строк

матриц S и Dr:

∑ si, j di, j (4.2) j =1

Номера (индексы) элементов упорядочивают по убыванию J={i1, i2,…, iN}, L1 ≥L2≥…≥LN. На очередном шаге алгоритма рассматривают возможные перестановки элемента ek с элементами из подмножества {ek+1,ek+2,…,eN}. После окончания цикла итераций подсчитывают новые значения Li и процесс может повториться.

Рассмотрим пункты итерационного алгоритма парных перестановок по мультиграфу схемы:

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-134-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

1.Определяется порядок просмотра элементов. Для существующего

размещения по формуле (4.2) определяется суммарная длина связей Li каждого элемента. Затем ранжируются индексы элементов по убыванию Li, т. е. формируется последовательность индексов элементов J={i1,i2,…,iN}.

2.Для следующего элемента последовательности ik Jk по формуле

(4.1) определяется приращение	Lik, j ;	j Jk+1 ={ik+1, ik+2,..., iN}.
3. Определяется Lik		,iq = max { Lik , j } .
		j J k +1
4. Проверяется условие	Lik ,iq > 0 . В случае выполнения условия в

последовательности J меняются индексы ik и iq. Если условие не выполняется, то осуществляется переход к п. 6.

5. Корректируется матрица Dr, т. е. переставляются строки и столбцы с

индексами ik и iq.

6. Проверяется условие окончания цикла итераций jk+1=0. Если условие выполняется, то осуществляется переход к п. 7, иначе полагают k=k+1 и переходят к п. 2.

7.	Проверяется условие окончания итерационного процесса
Lk −1 −	Lk	≤ε . В случае выполнения условия переход к п.8, иначе – к п.1.

8. Конец работы алгоритма.

Рассмотрим пример применения описанного алгоритма. В качестве исходных данных возьмем пример, представленный на рис. 4.50. Для рассматриваемого примера в качестве исходных примем следующие матрицы: S и Dr:

		1 3 2 4							e1	e1	e2	e3		e4
	1		0	1	1	2				0	0	1	1
										0	0	1	1
							,		e2	0	0	1	2		.
Dr=	3		1	0	2	1	,	S=	e2	0	0	1	2		.
Dr=	2		1	2	0	1		S=	e3	1	1	0	1
	2		1	2	0	1			e4	1	2	1	0
	4		2	1	1	0			e4	1	2	1	0

1. Вычисляем Li каждого элемента:

L1 = s12d13 + s13d12 + s14d14 = 0 +1+ 2 = 3 ;

L2 =s21d31 +s23d32 +s24d34 =0+2+2 =4;

L3 =s31d21 +s32d23 +s34d24 =1+2+1=4;

L4 = s41d41 +s42d43 +s43d42 =2 +2 +1=5.

Ранжируем индексы элементов по убыванию L:

J={4, 3, 2, 1}.

2. Для элемента 4 определяем приращение:

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-135-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.8.Алгоритмы размещения

L4,3 = ∑ (si,n −sj,n)(di,n −dj,n) = (s4,1 −s3,1)(d4,1 −d3,1) + (s4,2 −s3,2)(d4,2 −d3,2) =−1;

n=1,2

L4,2 =∑(si,n −sj,n)(di,n −dj,n) = (s4,1 −s2,1)(d4,1 −d2,1) + (s4,3 −s2,3)(d4,3 −d2,3) =1;

1,3

L4,1 = 0.

3.Определяем max(-1, 1, 0)=1, что соответствует элементу 2.

4.L4,2 > 0 , поэтому меняем местами в массиве J индексы: J={2, 3, 4,

1}.

5. Корректируем матрицу Dr:

						S
		1	3	4	2
	1	0	1	2	1
Dr=	3	1	0	1	2
Dr=	4	2	1	0	1
	4	2	1	0	1
	2	1	2	1	0	t

Рис. 4.51 Субблок с элементами кратных размеров

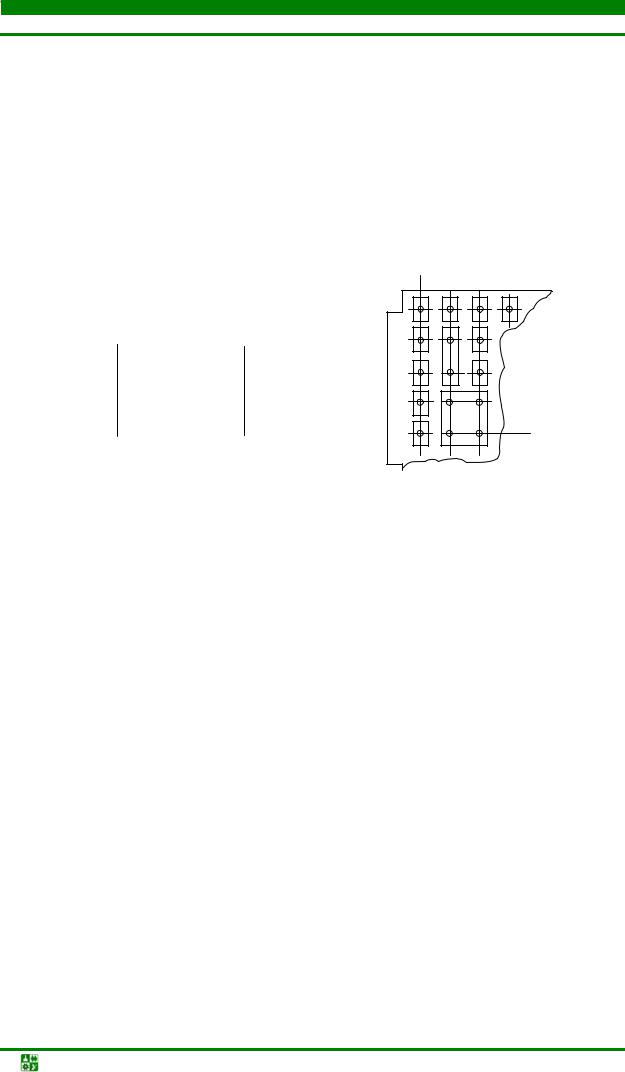
Описанные выше алгоритмы могут быть использованы для размещения разногабаритных элементов, размеры которых кратны или близки к кратным. При этом шаг установки выбирается в соответствии с размерами наименьшего конструктивного элемента (рис. 4.51). При размещении элемента, у которого хотя бы один размер больше размера позиции, в алгоритме необходимо проверять возможность установки элемента в рассматриваемую позицию. После размещения такого элемента в список занятых заносятся все занимаемые им позиции.

Нередко ручное размещение элементов конструктором создает лучшие условия для трассировки, чем машинное. При ручном размещении конструктор обычно стремится располагать в соседних позициях наиболее связанные элементы, входящие в функционально законченную группу, следя в то же время за достаточно равномерным распределением соединений по монтажному пространству. Эти принципы реализованы в ряде эвристических алгоритмов итерационного типа. Идея одного из таких алгоритмов заключается в последовательном разбиении схемы на две части, улучшении внутренней связности этих частей схемы и закреплении их за определенной областью монтажного пространства. Далее выполняется деление каждой части, т. е. процесс продолжается, пока не будет определена позиция каждого элемента. Для улучшения внутренней связности частей схемы может применяться итерационный алгоритм компоновки, использующий модель в виде гиперграфа. При некоторой его модификации можно учесть фактор «равномерного» распределения соединений.

Подробнее с алгоритмами размещения элементов можно познакомить-

ся в [13, 42, 43].

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-136-

4. ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9. Алгоритмытрассировкипечатногомонтажа

Уточним постановку задачи трассировки печатного монтажа, данную в параграфе 4.4 [13]. В монтажном пространстве, представляющем собой совокупность коммутационных плоскостей (см. рис. 4.29), определены координаты электрорадиоэлементов и их выводов, а также заданы параметры и топологические свойства монтажного пространства. Множество цепей принципиальной схемы разбивает множество B выводов на непересекающиеся подмножества Bi так, что

B{Bi / i =1, M} , а Bi ={bi,k / k =1, ki},

где М – число цепей, ki – число контактов, соединяемых i-й цепью. Необходимо реализовать множество Bi в виде множества Ai таких же

областей (см. рис. 4.52), которые удовлетворяли бы следующим требованиям:

Рис. 4.52. Реализация печатных соединений в монтажном пространстве

1. Ai E , все соединения должны быть выполнены в монтажной об-

i=1

ласти

E =	E	r	/ r = 1, R	,
		r

где R – число коммутационных слоев.

2. В каждом слое проводники не должны иметь пересечений:


A , A	j	E	A ∩ A			j
i	j		r	i		j
					i≠ j

= .

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-137-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

3.Расстояние между проводниками не должно быть меньше допустимого зазора ρ0 :

Ai , Aj Er (ρ (Ai , Aj )≥ ρ0 ).

4. Ширина проводника не должна быть меньше допустимой d0 : d (Ai )> d0 .

5. Все контакты i-й цепи должны лежать на i-м проводнике:

(Ai,k ≡ bi,k

6.Если необходимо выполнить переход со слоя r на слой t, то пересечение областей должно иметь размер, достаточный для конструктивной реализации межслойного перехода:

ir ( Aj Et )(Ai ∩ Aj = Ai ∩ Aj > Rn ), Er , Et E)

Внастоящее время задача одновременной оптимизации всех соединений пока окончательно не решена, в связи с чем трассировку сводят к последовательному построению безперекрестного леса (каждое дерево леса реализует соответствующую электрическую цепь) и определению конфигурации соединения. При этом система покрывающих деревьев должна быть размещена в монтажном пространстве типовой конструкции, заданной своей математической моделью (см. параграф 4.6).

Процесс трассировки печатных соединений можно представить в виде совокупности следующих этапов:

1.Определение порядка соединений внутри цепи.

2.Распределение соединений по слоям печатной платы.

3.Нахождение последовательности проведения соединений в каждом

слое.

4.Получение конфигураций проводников – синтез их геометрии.

Впроцессе трассировки используются следующие критерии:

1.Минимум суммарной длины всех проводников.

2.Минимум числа пересечений проводников.

3.Минимум изгибов проводников.

4.Минимум числа слоев многослойной печатной платы и переходов со слоя на слой.

5.Минимум длины параллельных участков соседних проводников.

6.Равномерное распределение проводников по монтажной области. Первый критерий позволяет уменьшить задержку сигналов по линиям

связи, второй, третий и четвертый – повысить надежность и технологичность изготовления печатной платы, пятый и шестой – повысить помехозащищенность реализуемого режима на печатной плате.

Для трассировки соединений применяют различные методы. Классификация методов приведена на рис. 4.53 [43]. Рассмотрим некоторые алгоритмы трассировки [13, 18, 41, 42].

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-138-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

4.9.1. ВолновойалгоритмЛииегомодификации

Идея волнового алгоритма Ли используется в большинстве алгоритмов построения конфигурации печатных проводников. Алгоритм представляет собой процедуру нахождения кратчайшего пути в графе. При использовании алгоритма Ли плоскость монтажа разбивают на элементарные квадраты со стороной, равной расстоянию между осями соседних проводников. При использовании ДПР включение элементарной ячейки в путь означает проведение печатного проводника так, как это показано на рис. 4.54, т. е. считается, что основная сетка смещена на h/2, чтобы пути следовали из ячейки в ячейку, а не по координатным линиям ДРП.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-139-

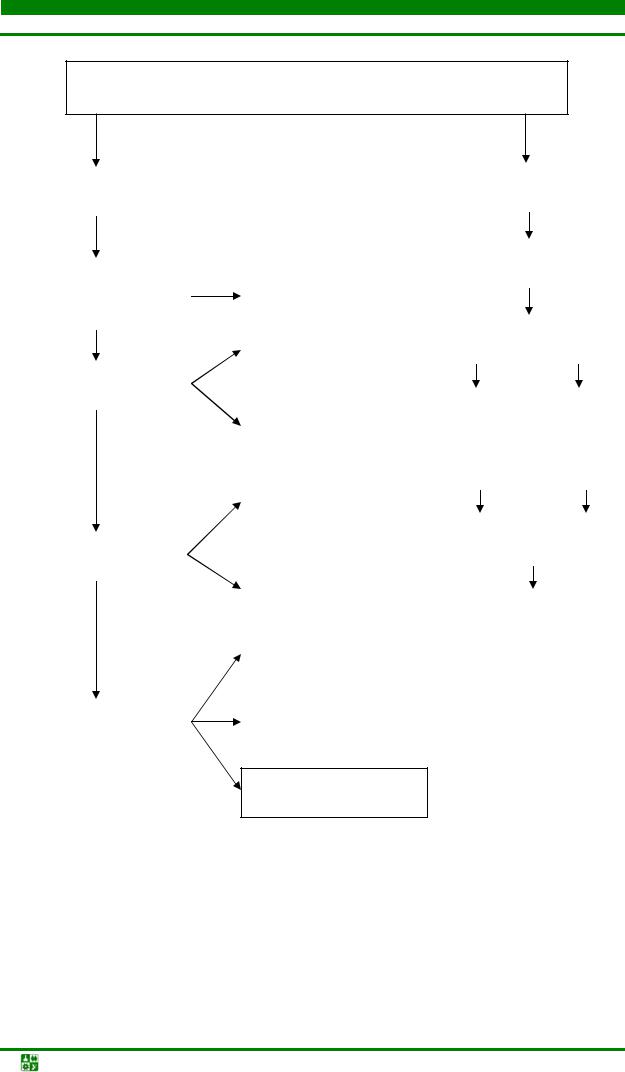
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

Алгоритмические методы трассировки соединений

Топографические методы		Графотеоретические
		методы



		Построение
Получение списка		графа схемы
Получение списка	Алгоритмы построения	графа схемы
соединений	Алгоритмы построения
	минимизации деревьев

(таблица проводов)
(таблица проводов)
		Анализ планарности
	Метод раскраски графа
	пересечения
Расслоение

	Ортогональное расслоение	Планариза-	Выделение
	с минимизацией	ция	плоских
	переходов		подграфов


	Оценка длин соединений,
	числа соединений и др.
	числа соединений и др.

		Изображение графа схемы
Очередность прокладки		на плоскости
соединений
	Динамические схемы
	упорядочения
	упорядочения	Получение эскиза
		Получение эскиза
		топологии
		топологии

	Волновой алгоритм
	Волновой алгоритм
	и его модификация


Трассировка соедине-	Трассировка
ний	по магистралям

Канальная трассировка

Рис. 4.53. Схема классификации алгоритмов трассировки

При волновом алгоритме ДРП, ПП представляется в виде набора ячеек. На каждом шаге алгоритма некоторые ячейки ДРП являются занятыми, к ним относятся ячейки попадающие в области запрещенные для трассировки (краевые поля, монтажные области ПП, зоны размещения некоторых ЭРЭ, зоны размещения выводов ЭРЭ, ранее проведенные проводники и т. п.)

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-140-

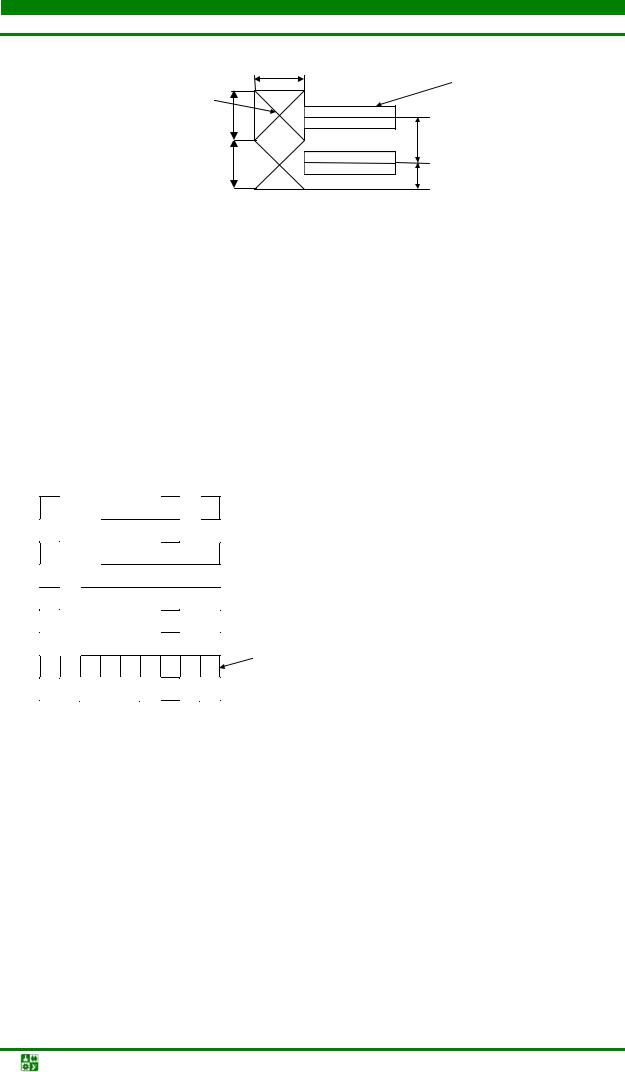
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

		h	Печатный
Ячейка	дискрет-		Печатный
Ячейка	дискрет-		проводник
ного рабочего по-
	h
			h
	h		/2
			h
Рис. 4.54. Схема плоскости монтажа при использовании алгоритма Ли

Алгоритм Ли ориентирован на нахождение оптимального, в смысле некоторого критерия пути между заданными ячейками ДРП (константами цепи) А и В, при соблюдении ряда условий. Алгоритм Ли можно представить в виде укрупненного алгоритма, состоящего из двух частей.

Первая часть алгоритма

Моделируется процесс распространения волны из ячейки А по свободным ячейкам ДРП. Распространяя волну от элементарной площадки А, алгоритм осуществляет последовательное распространение фронтов: Ф1(А) - первый фронт, Ф2(А) – второй фронт,…, Фk(А) – k-ый фронт (см. рис. 4.55). Множество ячеек, входящих в i-е фронты, для всех i ≤ k называют k-й окрестностью ячейки А-Оk(А).

			3
		3	2	3			Рис. 4.55. Процесс распространения волны:
	3	2	1	2	3		Рис. 4.55. Процесс распространения волны:
	3	2	1	2	3		“1”– 1-й фронт волны;
3	2	1	А 1		2	3	“1”– 1-й фронт волны;
3	2	1	А 1		2	3	“2”– 2-й фронт волны;
	3	2	1	2	3		“3”– 3-й фронт волны.
		3	2	3			ДРП
		3	2	3
			3

Проведение пути возможно тогда, когда на каком-то k+1 шаге окажет-

ся, что ячейка В Оk+1(А). В том случае, когда в следующий фронт не удается

включить ни одной свободной ячейки, т. е. Оk+1(А) = Оk(А), то при данных условиях путь провести невозможно. Таким образом, первая часть алгоритма

определяет возможность проведения пути между ячейками А и В ДРП. При распространении волны ячейкам присваивают веса Р. В общем случае

Рk-1≠Рk≠Рk+1.

Вторая часть алгоритма

Данная часть алгоритма ориентируется на то, чтобы начиная с ячейки В по определенным правилам выполнить переход от ячейки k-го фронта к ячейке k-1 фронта и т. д. до ячейки А. Пройденные таким образом ячейки составляют искомый путь. Условия, которые необходимо выполнить при проведении пути и возможность оценки его оптимальности, должны быть за-

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-141-

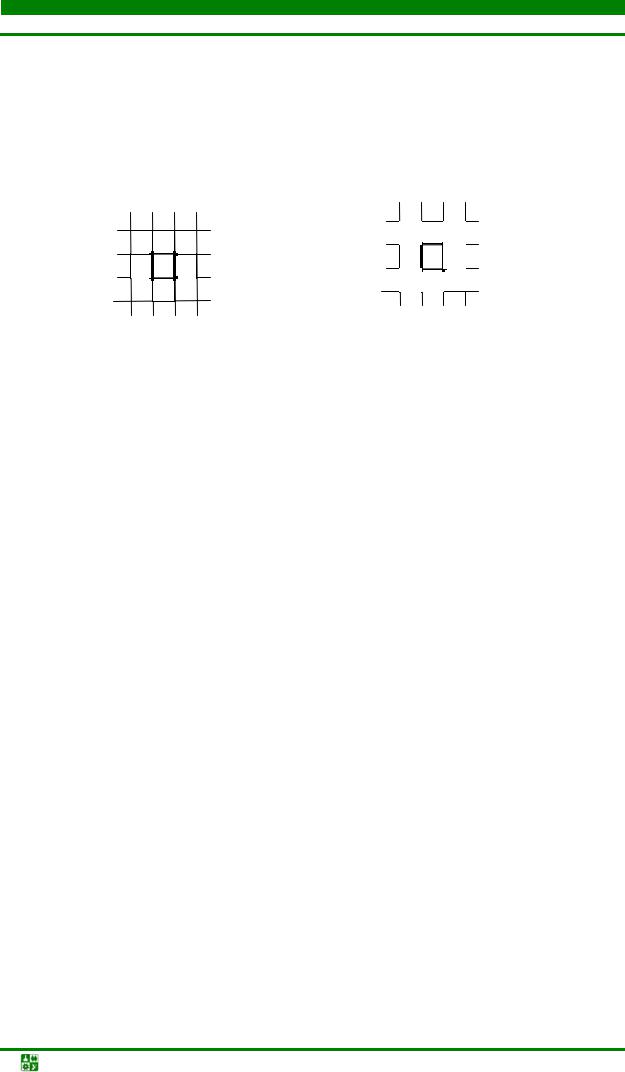
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

ложены в правила, по которым движется фронт волны. Для ячеек ДРП может быть установлено разное отношение соседства:

1.Общее ребро-ячейка соседствует по ребрам с соседними ячейками 1– 4, как это показано на рис. 4.56, а.

2.Общее ребро и вершина – в данном случае ячейка соседствует по ребрам и вершинам с соседними ячейками 1–8 (см. рис. 4.56, б).

Разные виды соседства влияют на структуру фронтов волны.

4		2
	3	а
		а

8	1	5
4		2
7	3	6
		б

Рис. 4.56. Формы соседстваРисячеек. 4.3ДРП. Соседство: «общее“общребро» (а)

вершинаребро вершина”

и «общее ребро и » – (б)

На данном шаге алгоритма также анализируются веса ячеек. В большинстве модификаций алгоритма Ли накладываются ограничения Рk>Рk-1. В этом случае проведение пути осуществляется от ячейки В к ячейке А таким образом, чтобы значение Рk монотонно убывало. Возможны ситуации, когда несколько ячеек соседних данной ячейке имеют одинаковые веса. В такой ситуации при учете критерия минимума изгибов проводников следует сохранить направление движения. Если при проведении пути приходится делать поворот, то учитывается заранее заданный порядок, предпочтительных направлений, например: вверх, вправо, вниз, влево.

Алгоритм Ли легко распространяется на многослойный печатный монтаж, при использовании модели в виде графа монтажного пространства. При наличии ограничений на переходы со слоя на слой можно увеличить вес ребра, соединяющего две смежные вершины на соседних слоях, по сравнению с весом ребра, соединяющего смежные вершины в одном слое. В общем случае весовая функция или критерий качества пути может зависеть от параметров, учитывающих длину пути, число переходов со слоя на слой, степень близости к другим и. т. д., например в виде аддитивной функции:

Pk = ∑ ai Pi (k),

k = 1

где ai – весовой коэффициент, учитывающий важность i-го параметра; Pi(k) – значение учитываемого параметра.

Усложнение функции веса увеличивает объем информации на одну ячейку ДРП и время работы первой части алгоритма. На практике является сложным строгое обоснование выбора значений весовых коэффициентов ai.

При практической реализации волнового алгоритма, важной проблемой является проблема сокращения объема оперативной памяти ЭВМ, необходимого для заполнения весов ячеек ДРП.

При вычислении весов ячеек, согласно выражению Рk = Рk-1+1, ячейка может быть в следующих состояниях: свободна, занята, иметь вес от 1 до L

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-142-

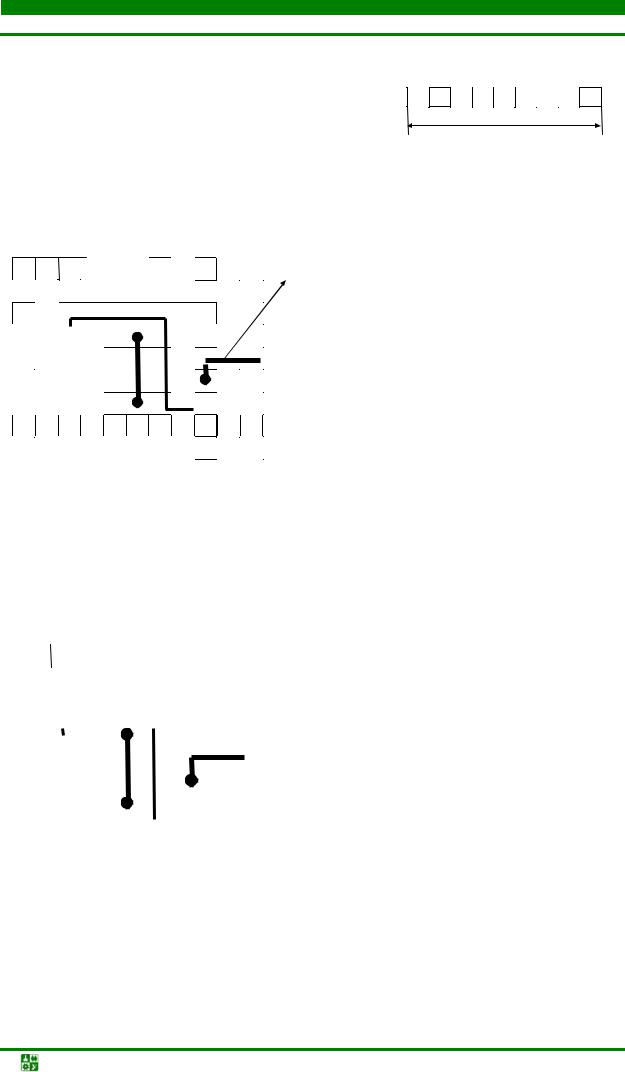
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

(где L – максимально возможная длина пути (рис. 4.57), определяемого как
количество составляющих его ячеек ДРП).
		Необходимое число разрядов памяти, для									1 2 3 4 5 6 7 8 9
запоминания состояния одной ячейки ДРП, вы-
числяется при этом как											L
						N = log2				(L+2) .	Рис. 4.57. Пример вычисления
		Пример построения минимального пути в									Рис. 4.57. Пример вычисления
ортогональной метрике приведен на рис. 4.58.											длины пути
ортогональной метрике приведен на рис. 4.58.
1	2	3	4	5	6	7	8	9	10	11
1 5	4	3	4	5	6	8	8	9		Запрещенные ячейки ДРП для трассировки
2 4	3	2	3	4	5	6	7	8	9
3 3	2	1	2	3	4	5	6	7	8
4 2	1	А	1	2		6	7	8	9
5 3	2	1	2	3		7	8			Рис. 4.58. Построение минимального пути
6 4	3	2	3	4		8	9			Рис. 4.58. Построение минимального пути
6 4	3	2	3	4		8	9			в ортогональной метрике: А – источник волны;
7 5	4	3	4	5		9	10			В – приемник волны; способ соседства ячеек –
8 6	5	4	5	6	7	8	9	10	11	“общее ребро”; предпочтительные направле-
9 7	6	5	6	7	8	9	10	11	12	ния – вверх, вправо, вниз, влево
		Наиболее эффективные способы кодирования состояния ячеек ДРП –
метод путевых координат, кодирование по модулю “3” и метод Акерса.

Метод кодирования по модулю "3"

Данный метод (рис. 4.59) базируется на основном требовании к весам:

Рk-1≠Рk≠Рk+1.

	1	2	3	4	5	6	7	8	9	10	11
1
1		2	1	2	3	1	2	3	1

2	2	1	3	1	2	3	1	2	2

3	1	3	2	3	1	2	3	1	3

4	3	2	1	2	3	1	2	3

5	2	1	А	1	2		3	1

6	3	2	1	2	3		1	2
7	1	3	2	3	1		2	3
8	2	1	3	1	2		3	1	В
9
9	3	2	1	2	3	1	2	3
10
10	1	3	2	3	1	2

Рис. 4.59. Пример работы алгоритма кодирования по модулю “3”: А – источник волны; В – приемник волны; предпочтительные направления (правила приоритетов) – влево, вверх, вправо, вниз

Ячейкам, включенным в последовательные фронты можно присваивать не сами веса, а их значения по модулю “3”, т. е. 1, 2, 3, 1, 2, 3..., при этом количество разрядов на кодирование состояния ячеек:

N = log2 5 = 3.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-143-

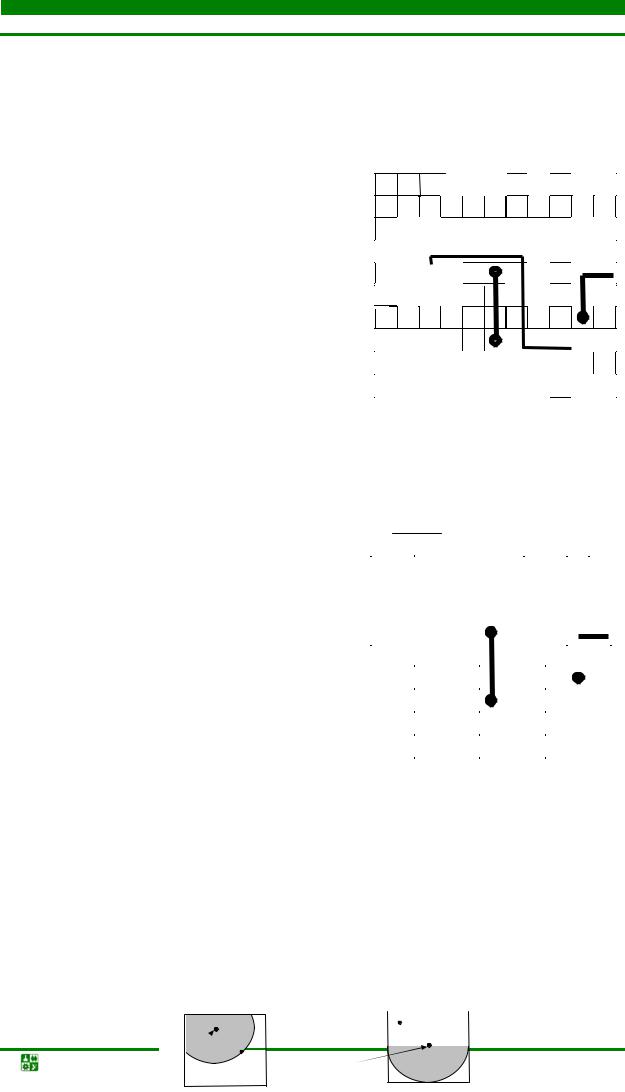
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

Проведение пути заключается в отслеживании отметок. В случае появления ячеек с одинаковыми отметками применяется правило приоритетов.

Метод путевых координат

При использовании метода путевых координат (рис. 4.60) для каждой ячейки, начиная с В, в случае соседства по ребрам достаточно знать, от какой соседней ячейки в нее пришла волна: сверху ↓, слева →, справа ←, снизу ↑.

При этом ячейка может иметь следующие признаки: свободна, занята или одну из путевых координат →, ←, ↓, ↑. Число разрядов на кодирование состояния ячеек

N= log2 6 = 3.

При проведении трассы используется правило приоритетов.

1	2	3	4	5	6	7	8	9	10	11

3 ↑ ↑ ↑ → → → → → →

4 ↑ ↑ ↑ → → → ↓ ↓ ↓

5 ← ← А → → ↓ ↓ ↓

6 ↓ ↓ ↓ ↓ ↓ ↓ ↓

7 ↓ ↓ ↓ ↓ ↓ ↓ ↓

8 ↓ ↓ ↓ ↓ ↓ ↓ B

9 ↓ ↓ ↓ → → → → → →

10 ↓ ↓ ↓ ↓ ↓ ↓

Рис. 4.60. Метод путевых координат

Метод Акерса

В методе Акерса (рис. 4.61) ис-
В методе Акерса (рис. 4.61) ис-			1	2	3	4	5	6	7	8	9	10	11
пользуется идея, что для определения			1	2	3	4	5	6	7	8	9	10	11
	1				2

последовательности ячеек, составляю-

	2				2	2
щих путь, достаточно, чтобы при рас-	2				2	2
	3				1

пространении волны ячейкам присваи-
	4			1	1	1	2	2

вались значения отметок из заданной
вались значения отметок из заданной					А
последовательности, в которой каждый	5		1	1		1	1
последовательности, в которой каждый	5		1	1		1	1
член имеет разных соседей слева и		6		1	1	1	2
справа. В методе используется после-	7		2	2	1	2	2
справа. В методе используется после-	7		2	2	1	2	2
довательность 1, 1, 2, 2, 1, 1 и т. д.	8		1	1	2	1	1					B
При построении пути находят	9				2
ячейки, входящие в заданную последо-	10
вательность. В методе количество раз-				Рис. 4.61.			Метод Акерса
рядов памяти на одну ячейку				Рис. 4.61.			Метод Акерса
рядов памяти на одну ячейку

N= log2 4 = 2.

Если построение последовательности возможно по нескольким направлениям, то используют правило приоритетов.

Волновой алгоритм характеризуется высокой эффективностью нахождения пути за счет исследования всех свободных ячеек ДРП, но требует значительного времени на распространение волны. В связи с этим используют различные методы ускорения первого этапа алгоритма, например выбор на-

	Автоматизация проектирования РЭСВ.	В	-144-
	Автоматизация проектирования РЭСВ.	Топологическое проектирование печатных плат. Учебное пособие

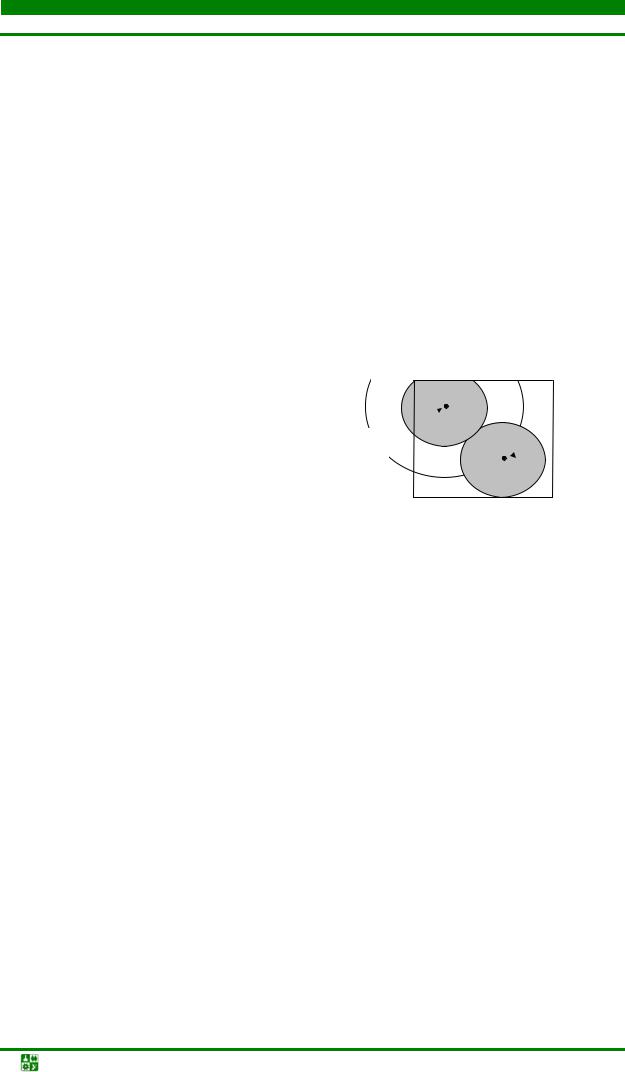
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

чальной точки (см. рис. 4.62).

Рис. 4.62. Выбор начальной точки

Из рис. 4.62 видно, что при выборе в качестве источника (“A”) распространение волны площадки, максимально удаленной от центра платы, просматривается меньшее число свободных ячеек ДРП (по мере роста числа разведенных цепей это становится не очевидным, поэтому данный подход хорош на начальной стадии разводки).

Более эффективным является метод встречной волны (рис. 4.63). Выигрыш по времени пропорционален отношению числа исследуемых ячеек при одновременном распространении волны из одного источника. При непрерывной модели окрестности волны на свободном поле ДРП отношение исследуемых площадей:

M = πr2 / [2π (r/2)2 ] = 2.
M = πr2 / [2π (r/2)2 ] = 2.
Для реальных состояний выигрыш
во времени может отличаться, однако в			В
среднем оценка является объективной.	А		В
Пример метода приведен на рис. 4.64.	А
Поле распространения волны мож-
Поле распространения волны мож-
но уменьшить, ограничивая его прямо-
угольником, внутри которого находятся		Рис. 4.63. Схема метода
соединяемые площадки (начальная пло-			встречной волны

щадь прямоугольника обычно на 10–20% больше площади прямоугольника, проходящего через эти площадки, – один из вариантов).

Если соединения найти не удалось, то границы прямоугольника расширяют на одну единицу ДРП во все стороны. Данный метод по эффективности превосходит вышеописанный. Рассмотрим пример одного из возможных вариантов метода встречной волны (рис. 4.65)

1.Определяют координаты источника и цели (ячейки «4» и «9»).

2.Определяют ячейки ДРП, которые являются препятствием.

3.Определяют первоначальные границы источника и цели.

4.Расширяют границы источника и цели на одну ячейку со всех сто-

рон.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-145-

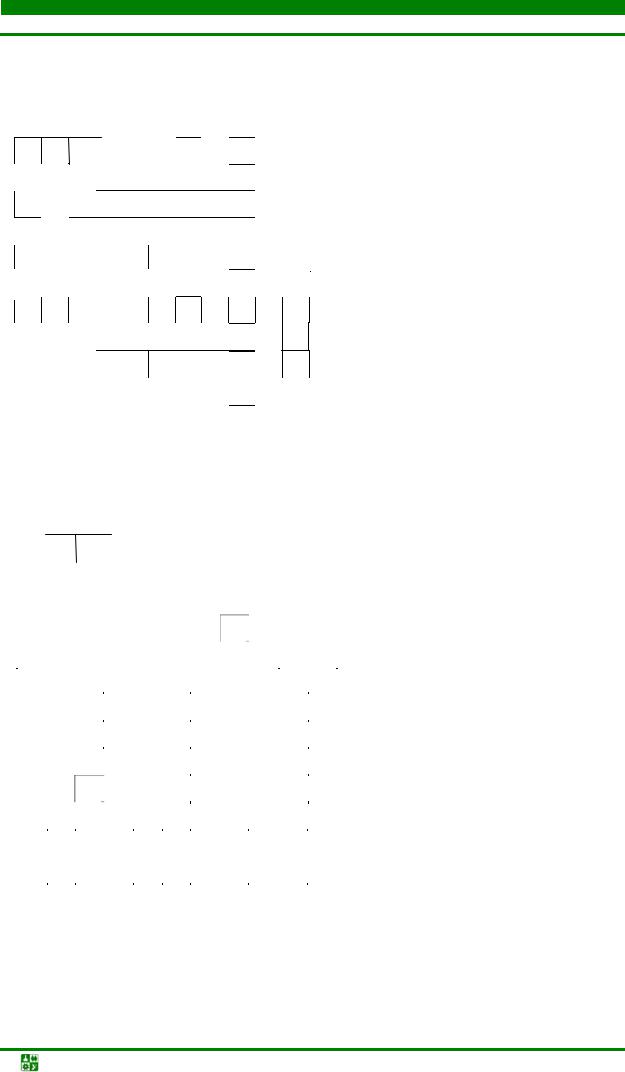
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

5.Просмотрев ячейки расширенных областей расширяют области еще на 1 ячейку, со всех сторон и т.д.

	1	2	3	4	5	6	7	8	9	10	11
1		1	3	1	2
2	1	3	2	3	1	2
3	3	2	1	2	3
4	2	1	‘4’	1	2	3	1	7	6
5	3	2	1	2	3	1	7	6	8	6	7
6		3	2	3	1	7	6	8	7	8	6
7						6	8	7	6	7	8
8					6	8	7	6	‘9’	6	7
9						6	8	7	6	7	8
10							6	8	7	8	6

‘4’– источник. ’9’–цель.

‘5’–препятствие. волны:

от ‘4’ - 1, 2, 3, 1, 2, 3,...

от ‘9’ - 6, 7, 8, 6, 7, 8...

Алгоритм метода:

1-й шаг. от ‘4’ →1 затем от ‘9’→6 2-й шаг. от ‘4’ после 1→2, затем от ’9’ после 6→7 и т. д.

Проведение трассы осуществляется в двух направлениях: от места встречи к цели и к источнику.

Рис. 4.64. Пример распространения встречных волн

			1			2	3	4	5	6	7	8	9	10	11
1
1
2
2										6	8	7	8	6

3										8	7	6	7	8

4										7	6	9	6	7

5										8	7	6	6	8

		6								6	8	7	8	6
																Первое расширение волны:
7			2			1	3	1	2	3						Первое расширение волны:
																от источника ‘1’ и от цели ‘6’
8			1			3	2	3	1	2						от источника ‘1’ и от цели ‘6’
8			1			3	2	3	1	2						от источника ‘2’ и от цели ‘7’.
																от источника ‘2’ и от цели ‘7’.
9			3			2	1	2	3	1						Анализируется по 9 ячеек.
																Второе расширение:
10			2			1	4	1	2	3						Второе расширение:
10			2			1	4	1	2	3						аналогично,	только	от ис-
																аналогично,	только	от ис-
	11				3	2	1	2	3	1						точника ‘2’, ’3’, ’1’		и от цели
	11															точника ‘2’, ’3’, ’1’		и от цели
12					1	3	2	3	1	2						‘7’, ‘8’, ‘6’	и т. д.

13				2		1	3	1	2	3

Рис. 4.65. Пример модифицированного метода встречной волны

Теперь рассмотрим пример работы волнового алгоритма для всей цепи

(рис. 4.66).

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-146-

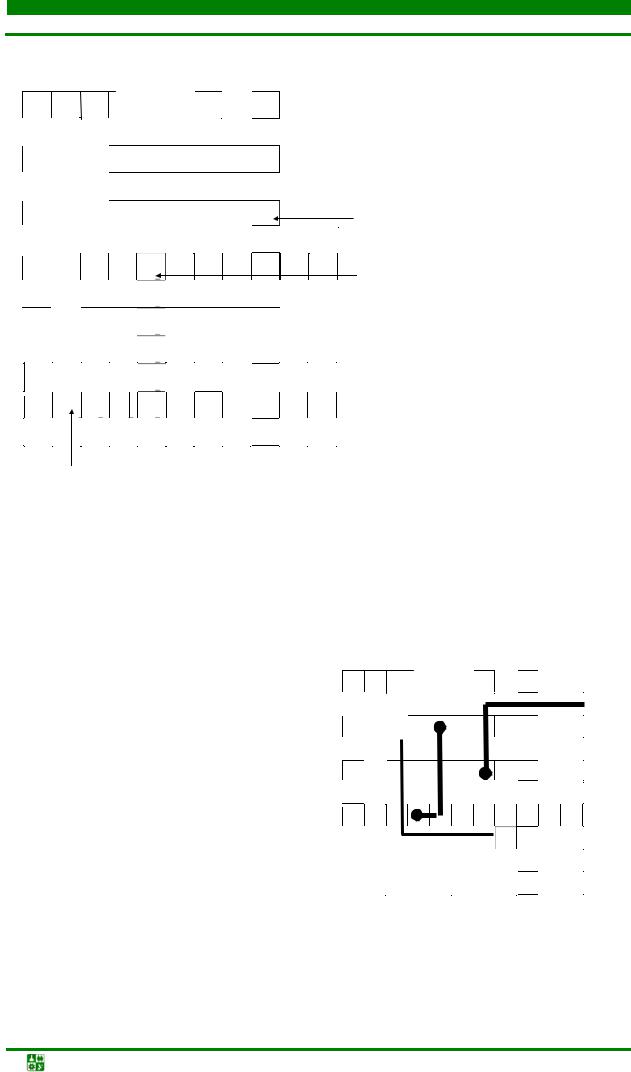
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

1	2	3	4	5	6	7	8	9	10	11
1
2
3
4							7	6	7
5							6	9	6	С
5			2	1	2	3	7	6	7	С
6			2	1	2	3	7	6	7
7			1	4	1	2	3			В
			1	4	1	2	3			В
8			1	4	1	2	3
9			1	4	1	2	3			Рис. 4.66.	Пример построения трассы
10			1	4	1	2	3			методом встречной волны для всей
10			1	4	1	2	3			цепи: А, В, С - контакты одной цепи
11	1	1	1	4	1	2	3			(А и В	были соединены на первом
11	1	1	1	4	1	2	3			шаге. Далее соединяются С и полу-
										шаге. Далее соединяются С и полу-
12	4	4	4	4	1	2	3			ченная трасса)
13	1	1	1	1	2	3	1

Если цепь состоит из нескольких контактов, то сначала соединяются

два контакта цепи (1-й контакт – источник, 2-й – цель). Все другие контакты

при этом играют роль препятствий. Далее ячейкам, в которых находились 1-й

и 2-й контакты, а также ячейкам, по которым проведена была трасса, при-

сваивается вес источника (в нашем случае ‘4’). Теперь целью становится 3-й

контакт цепи. После соединения с первыми двумя контактами

аналогично

наращивается число ячеек с весом ‘4’ и т. д.

4.9.2. АлгоритмАбрайтиса

Другая идея ускорения поис-

А1

А →

↑

ка пути заключается в исследова-

А2

нии не всех ячеек ДРП, а лишь

по

↓

↑

заранее

заданным

направлениям

↓

↑

(→). Одним из таких алгоритмов

↓

↑

В1

является лучевой алгоритм Абрай-

↓

↑

тиса [19]. В данном алгоритме, для

↓

← ← ← ← В

площадок А и В

(рис. 4.67) за-

↓

В2

дают

количество

распространяе-

↓

мых лучей и разрешенные направ-

ления их движения. При прохожде-

Рис. 4.67. Метод Абрайтиса. Правила движения:

нии луча через ячейку ей присваи-

А1: → и ↓; A2: ↓ и →; B1: ↑ и ←;

B2: ← и ↑

вают лучевую координату.

На рис. 4.67 приведен пример пути двухлучевым алгоритмом. На приве-

денном рисунке лучу А1 разрешено движение вправо и

вниз, лучу А2 – вниз и

вправо, лучу В1 – вверх и влево, лучу В2 – влево и вверх.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-147-

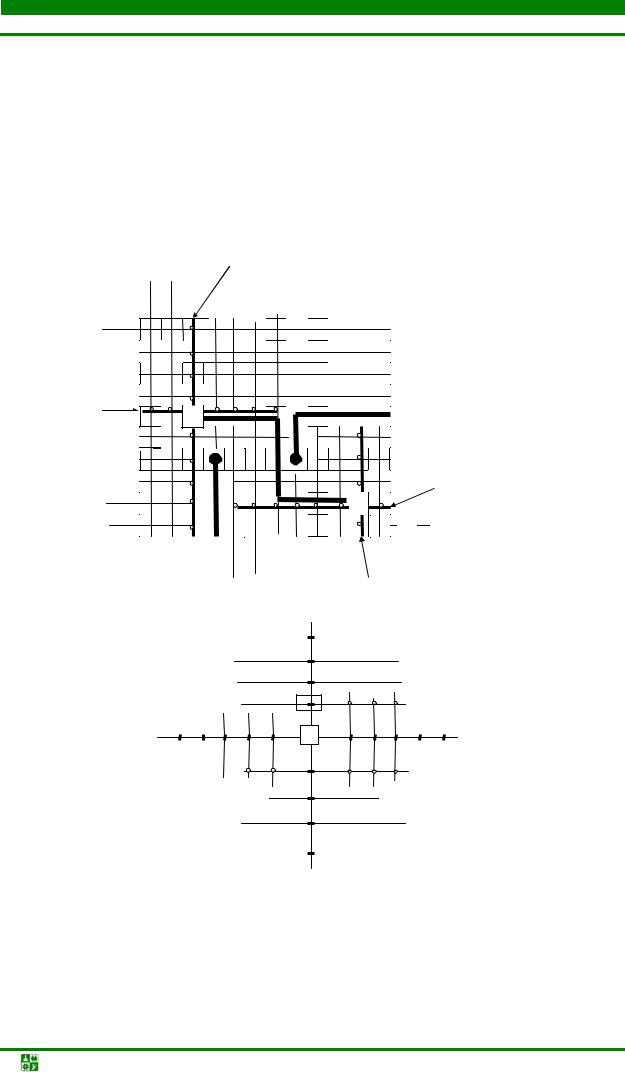
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

Вероятность проложения пути данным алгоритмом ниже, чем при ис-

пользовании волнового алгоритма.

4.9.3. Алгоритмтрассировкипомагистралям

Данный алгоритм близок к лучевому алгоритму. Из площадок А и В по

свободным ячейкам ДРП проводят

горизонтальные и вертикальные лучи

(см. рис. 4.68) до их встречи или до препятствий.

Если магистрали МА1 и МВ1 не пересекаются, из ячеек, расположенных

MA2

MA1

9 10

11 12

MA1, MB1 –

магистрали

1-го уровня

MA1

MA2, MB2 –

магистрали

MB1

MA2

MB2

.............

MB1

Вертикальный
луч (магистраль)
MA1
Горизонтальный
луч (магист-
раль)
А
MA2	MA2
:	б
:

Рис. 4.68. Пример работы алгоритма по магистралям: общий вид ДРП (а);

схема распространения лучей (магистралей) 2 – го уровня (б)

на этих направлениях проводят магистрали второго уровня МА2 и МВ2 (рис. 4.68, б), причем МА2 и МВ2 ортогональны МА1 и МВ1 соответственно. Пусть существует, если магистрали МА и МВ некоторого уровня пересекаются, и не существует – в противном случае.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-148-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

4.9.4. Алгоритмгибкойтрассировки

Алгоритм основан на том, что конфигурация всех трасс рассматривается одновременно и предусматривается возможность воздействия одной трассы на другую.

В исходном состоянии дискреты каждого вывода образуют отдельные области, расширяющиеся в процессе трассировки за счет свободных дискретов либо дискретов других областей. Каждая область составляет фрагмент некоторой цепи и имеет определенный приоритет, согласно которому она может “отбирать” дискреты только из области с низким приоритетом. В конечном итоге если все цепи будут иметь по одной области, то трассировка завершается успешно. Для управления процессом трассировки вводятся следующие правила:

1.Несоединенные цепи должны иметь более высокий приоритет, чем соединенные.

2.Областей с одинаковым приоритетом не должно быть.

3.От областей чужой цепи нельзя “отбирать” дискреты ее выводов.

4.Построенные соединения нельзя разъединять.

Для равномерного расширения областей просмотр дискретов проводится в шахматном порядке, т. е. все дискреты делятся на “белые” и “черные” и просматриваются поочередно.

1	2	3	4	5	6
1
2	А	А	А	А	А
3	В		х
4			х		В

Пример.			Необходимо соединить выводы це- Рис. 4.69. Пример ДРП
пей А и В (две цепи А и В на рис. 4.69). Обычный
1	2	3	4 5	6	волновой алгоритм не дает решения, так
1	A			A	как после проведения цепи А цепь В бло-
					кируется.
2 A	А	A	А	А

3	BВ			A
4			BВ В
Рис. 4.70. 1-й шаг алгоритма					Алгоритм трассировки в общем виде
гибкой трассировки

	1	2	3	4	5	6
1	А Aa		А		А	А
2	А А		А	А	А	А
3	В В		В		В	А
4		В			В	В

Рис. 4.71. Соединение выводов А

1. После первого сканирования обе цепи расширяются на черные дискреты

(рис. 4.70).

2. Цепь А имеет более высокий приоритет, т. к. расстояние между контактами короче.

3. После второго сканирования выводы цепи А соединяются и ее приоритет становится ниже (второе сканирование по белым клеткам – рис. 4.71).

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-149-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

	1	2	3	4	5	6
1	А	А А		А	А	А
2	В А		В	А	В	А
3	В В		В		В	В
4	В	В	В		В	В

Рис. 4.72. Перераспределение дискрет

4. При третьем сканировании цепь В отбирает некоторые дискреты от цепи А (рис. 4.72).

	1	2	3	4	5	6
1	В	А А		А	А	А
2	В А		В	В	В	А
3	В	В	В		В	В
4	В	В	В		В	В

Рис. 4.73 Результат трассировки

5. При четвертом сканировании выводы цепи В соединяются (рис. 4.73).

Рассмотренный алгоритм применяется на заключительных этапах трассировки и перетрассировки сложных плат с регулярной структурой элементов или больших интегральных схем.

4.9.5. Алгоритмыканальнойтрассировки

Данный алгоритм относится к самостоятельному классу алгоритмов. Алгоритмы ориентированы на построение монтажных трасс в таких монтажных пространствах, где между рядами и столбцами элементов можно провести совокупность горизонтальных и вертикальных магистралей (рис. 4.74). Объектами трассировки для данных алгоритмов являются большие гибридные и интегральные схемы, некоторые типы функциональных ячеек и печатных узлов и т. д.

Совокупность магистралей называют каналом. Монтажное пространство таких объектов представляет собой последовательность горизонтальных и вертикальных отрезков магистралей c переходными контактами со слоя на слой в местах сопряжения этих отрезков (рис. 4.75).

В алгоритмах канальной трассировки можно выделить две основные части:

1.Распределение отрезков трасс по каналам с учетом их равномерной загрузки .

2.Определение места нахождения отрезков на магистралях.

Во 2-й части алгоритма для каждой цепи строят возможные на данной системе каналов ортогональные деревья Штейнера (см. рис. 4.76), т. е. определяют сеть возможных каналов цепи.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-150-

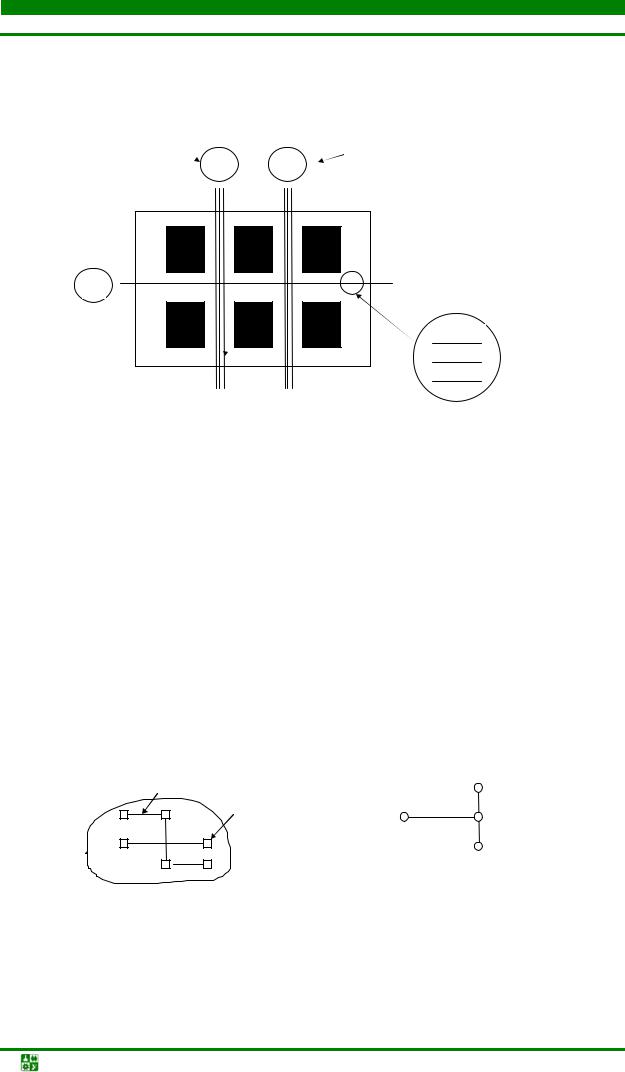
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

При наложении сетей отдельных цепей на основную сеть каналов выбирают те реализации связующих деревьев, которые обеспечивают равномер-

ную загрузку каналов, например, как это показано на рис. 4.77.

1-й вертикаль-				2-й вертикаль-
ный канал	1		2	ный канал

1 1-й горизонталь-

ный канал

h1 h2 h3

Канал

Вертикальные каналы магистрали

Рис. 4.74. Монтажное пространство при использовании алгоритма канальной трассировки: h1, h2, h3 – горизонтальные магистрали; пропускная способность каналов (в данном примере) равна 3

Так как отрезок цепи может занимать не всю длину магистрали, число проводников, назначенных в канал, может превышать число его магистралей.

Во второй части алгоритма для определения положения отрезков на магистралях множество отрезков (М), отнесенных к каналу, разбивают на К ≤ m непересекающихся множеств Mi (i I/i=1,k). При этом проводники, отнесенные к одной магистрали, т. е. включенные в подмножество Mi, не должны перекрываться, чтобы не было наложения отрезков разных цепей.

Существует несколько алгоритмов распределения отрезков по магистралям канала.

Отрезок

Контакт

Рис. 4.76. Пример ортогонального дерева Штейнера

Рис. 4.75. Фрагмент монтажного пространства

Рассмотрим алгоритм последовательного заполнения магистралей (модификация метода интервалов).

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-151-

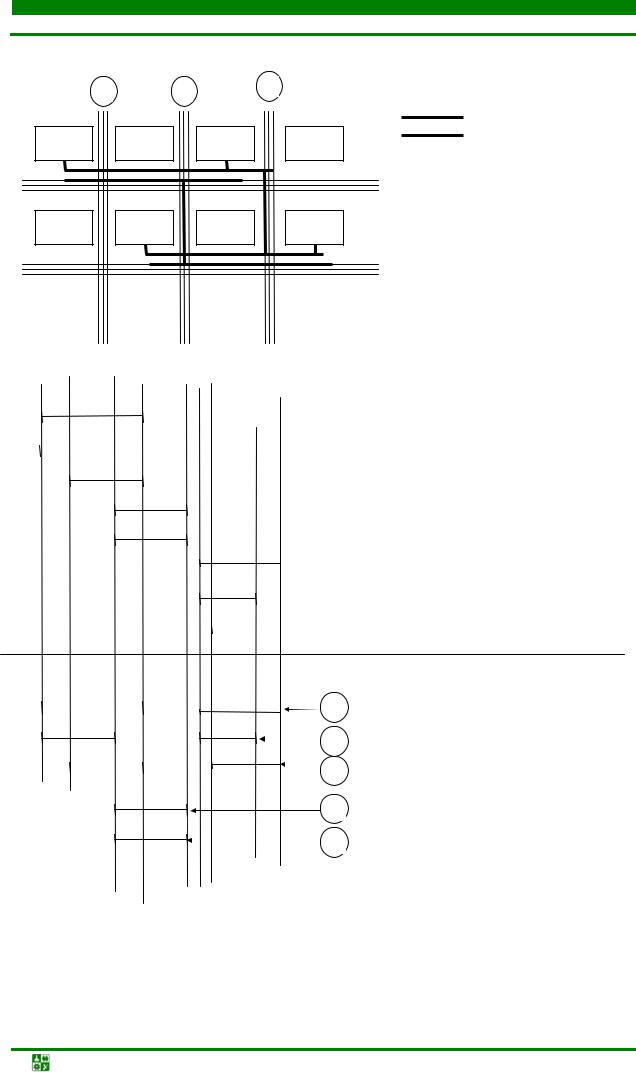
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

– 1-й вариант

– 2-й вариант

1-й вариант – занята часть магистрали 3-го вертикального канала. 2-й вариант – занята часть магистрали 2-го вертикального канала.

Рис. 4.77. Пример построения сети

каналов

М = m1, m2, m3, m4, m5, m6, m7, m8

В результате получаем:

M1 = m1, m5, m7, m3, m6, m2, m8, m4

M1 = m1, m2

M2 = m5, m8

M3 = m7, m4

M4 = m3

M5 = m6

Рис. 4.78. Упорядочивание множества М отрезков

Суть алгоритма заключается в том, что формируются подмножества Mi, путем последовательного включения в них тех отрезков, у которых начальная координата больше конечной координаты предыдущего отрезка.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-152-

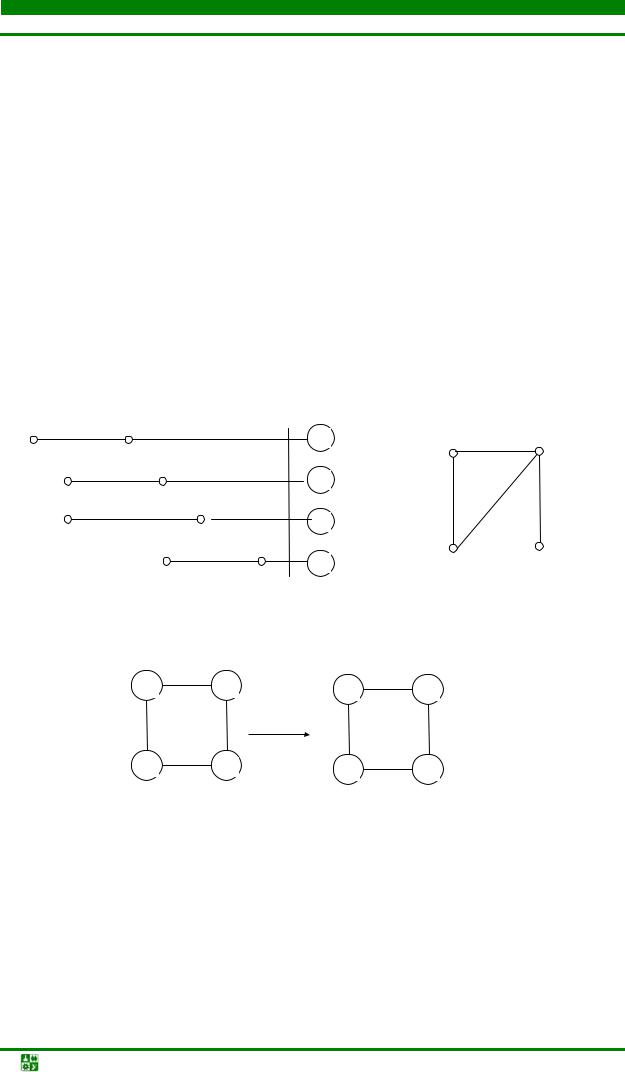
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

Пример. Дано 8 отрезков: m1 – m8. На первом этапе упорядочивается множество М (см. рис. 4.78, а). На втором этапе формируем множества

М1 – М5 (см. рис. 4.78, б).

Метод интервалов (постановка задачи)

Дано некоторое множество горизонтальных отрезков цепей (интервалов) M= m1, m2,.....mn , отнесенных к одному каналу (рис. 4.79). Каждый отрезок задается координатами его концов mi = [x11, x21]. Два отрезка считаются пересекающимися и не могут быть помещены на одну магистраль, если Мi∩ mj ≠. Графом интервалов Gu(M, U) множества М называется граф, вершины которого соответствуют интервалам mi, а наличие ребер Uij=(mi, mj) соответствует пересечениям интервалов mi и mj.

Задача оптимального использования магистралей заключается в решении задачи получения минимального количества цветов раскраски вершин графа Gu (рис. 4.80) таким образом, чтобы смежные вершины были окрашены разными цветами (рис. 4.81).

m1		1	m1	m3
		1	m1	m3
m2		1
		1
m3		1
		1
m4		1	m2	m4
		1
Рис. 4.79. Расположение отрезков цепей			Рис. 4.80. Граф интервалов
в канале			Рис. 4.80. Граф интервалов
в канале
m1	m3	m1	m3
К	C	К	C

Б	Ж	Б	К
m2	m4	m2	m4

Рис. 4.81. Раскраска вершин графа: К – красный; С – синий; Б – белый; Ж – желтый

Ширина канала кроме плотности соединений в нем зависит еще и от вертикальных ограничений на проведение соединений. При распределении горизонтальных отрезков цепей необходимо следить за тем, чтобы вертикальные отрезки разных цепей, имеющих одинаковую координату по сои X не перекрывались друг с другом. Это приводит к тому, что на расположение горизонтальных отрезков цепей существуют определенные вертикальные ог-

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-153-

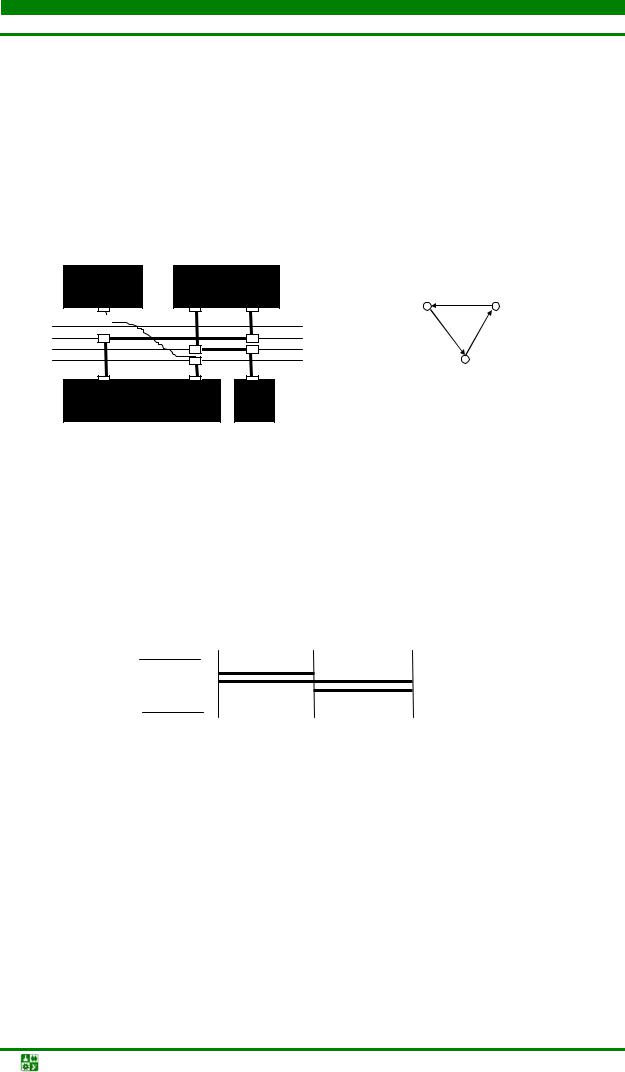
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

раничения (см. рис. 4.82). Вертикальный отрезок цепи v1 должен быть расположен выше вертикального отрезка цепи v3.

Указанные ограничения задаются с помощью ориентированного графа

Gb(V, U).

Вершинам графа соответствует горизонтальные отрезки цепей Vi, а наличие дуги Uij=(Vi, Vj) означает, что отрезок цепи Vi должен быть расположен выше отрезка цепи Vj.

Для приведенного на рис. 4.82 примера граф вертикальных ограничений будет иметь вид, приведенный на рис. 4.83.

v1 v3

Рис. 4.83. Граф вертикальных ограничений для схемы, изображенной на рис. 4.82

Рис. 4.82. Образование вертикальных ограничений

Контур в графе приводит к невозможности реализации соединений. Для решения данной задачи пронумеруем контакты номерами цепей, которым они должны принадлежать (рис. 4.84).

	Элемент				Элемент

		1	v1		2	v3		3
		1	v1		2			3
Канал
Канал						v2
3				1		v2	2
3				1			2

		Элемент					Элемент

Рис. 4.84. Пример соединения контактов ячеек

Канал рассматривают слева направо. При появлении пары контактов, лежащих на одной вершине (i-й вверху, а j-й внизу) формируется ограничение ni < nj (n – номер магистрали, нумерация магистралей сверху вниз).

Для примера на рис. 4.84: n1<n3, n2<n1, n3<n2 и v3>v1, v1>v2, v2>v3.

Ликвидировать контур можно следующим образом:

1)изменением размещения ячеек на ДРП;

2)делением горизонтальных отрезков цепей на части.

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-154-

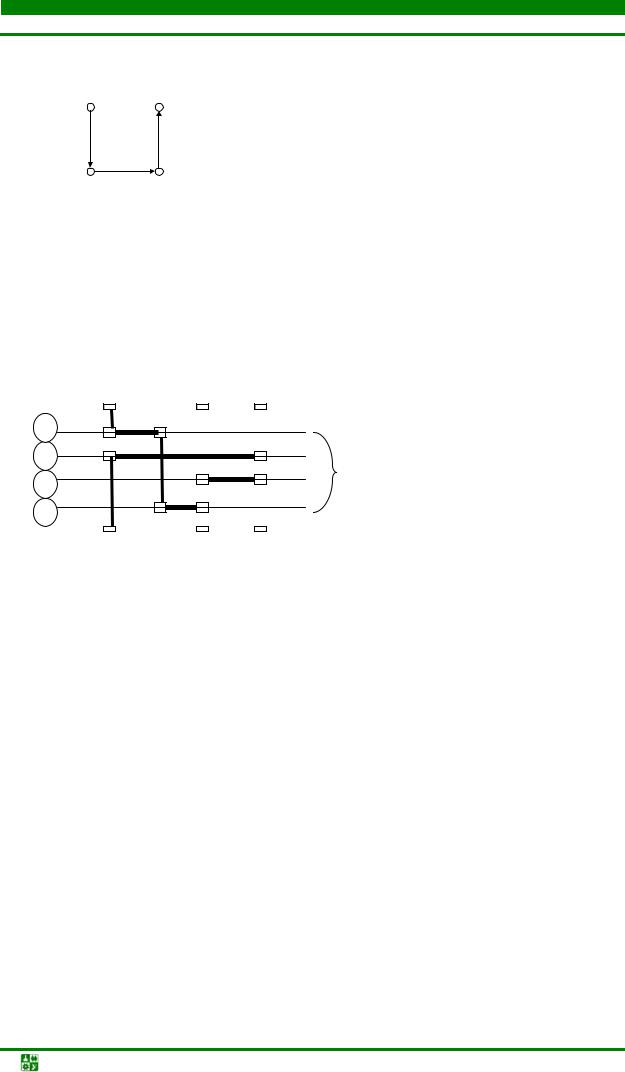
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

Пример: цепь V1 разбита на две части ( V1’ и V1’’ на рис. 4.85).

V1’	V1’’	Магистраль, в которой отрезок цепи
		V1’ больше магистрали V3; V3 >V2;
		V2 >V1’’.

V3 V2

Рис. 4.85. Бесконтурный граф

С учетом полученного графа трассируем соединения элементов, как это показано на рис. 4.86.

Горизонтальные отрезки – один слой

(1-й слой)

’

Магистрали канала

v1’’

Вертикальные отрезки – другой слой

(2-й слой)

Рис. 4.86. Трассировка элементов с учетом бесконтурного графа

Если обозначить lmax – число вершин в наибольшем ориентированном графе (бесконтурном), а tmax – максимальную плотность соединений в канале, то минимальную ширину Н канала можно определить следующим образом:

Н = max(tmax, lmax ).

Минимизация площади, занимаемой соединением канала, сводится к минимизации ширины канала и определяется плотностью соединений и структурой вертикальных ограничений.

Рассмотрим пример работы всего алгоритма канальной трассировки. 1. Дано несколько элементов и схема соединений их контактов

(рис. 4.87).

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-155-

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

Элемент				Элемент				Элемент

	1	2			1	2			3
	1	2			1	2			3
		4	3				4



Элемент				Элемент				Элемент

Рис. 4.87. Пример разположения элементов и контактов

2. Строим схему канала (рис. 4.88).

Рис. 4.88. Схема канала

3. Формируем диаграмму горизонтальных отрезков цепей (рис. 4.89).

1	2	1	2	3
		m1
		m2
				m3
			m4
	4		3	4

Рис. 4.89. Диаграмма горизонтальных отрезков

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-156-

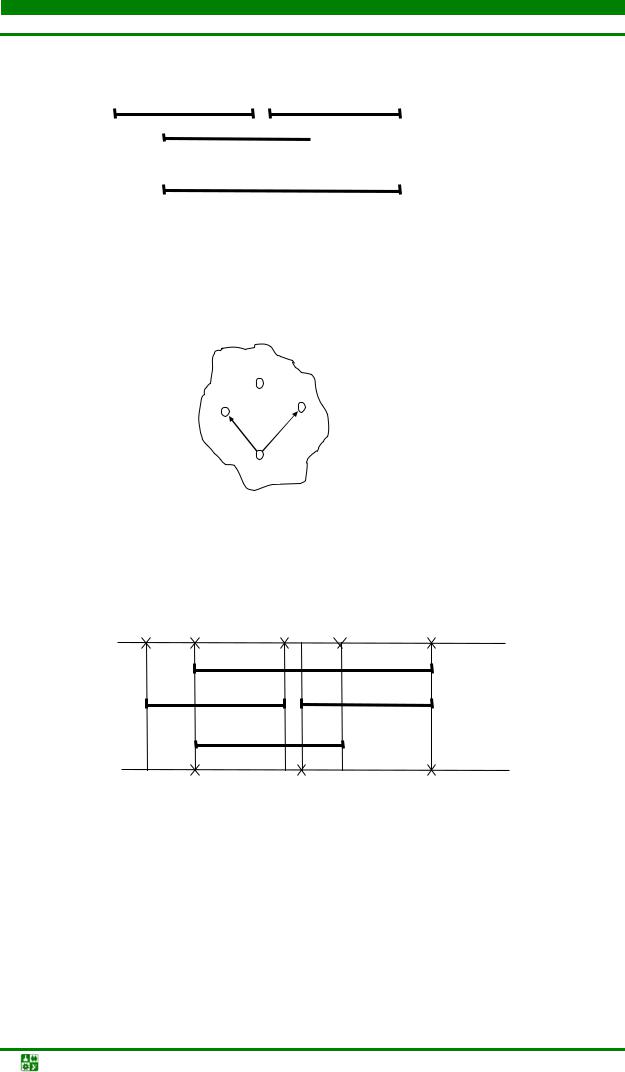
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ

4.9.Алгоритмы трассировки печатного монтажа

4.Заполняем магистрали (рис. 4.90).

m1 m3

m2		M1=(m1,m3)
		M2=(m2)
m4

		M3=(m4)

Рис. 4.90. Схема заполнения магистралей

5. Формируем структуру вертикальных ограничений n2<n4 и n3<n4, т. е. m2<m4 и m3<m4 и строим граф вертикальных ограничений (рис. 4.91). Из рисунка видно, что контуров в графе нет.

Рис. 4.91. Граф вертикальных ограничений

6. Получаем окончательный результат трассировки, который приведен на рис. 4.92.

1	2	1	2	3
			m4
	m1		m3
		m2
	4		3	4
	Рис. 4.92. Схема трассировки канала

Более детально с алгоритмами трассировки можно ознакомиться в [13, 17, 18, 41, 42, 43].

Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие

-157-

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в папке Учебники по PCAD

#
27.03.2016116.37 Кб41Altium_Winter_09.pdf
#
27.03.20165.63 Mб75P-CAD_2001_Russian_User_Guide.pdf
#
27.03.2016326.39 Кб36SUGGESTED PAD LAYOUT.pdf
#
27.03.20161.22 Mб78The CAD Library of the Future.pdf
#
27.03.20163.11 Mб135Автоматизация проектирования РЭС_Топологическое проектирование печатных плат_Кофанов_2008.pdf

				3
1	&	9	&	1			12
1		9					12
				4
2	3	10	8	4
2		10			1		11
					1

4	&	1	&	5
	&		&
	6		1				1
	6		1	1			1
5		1				10	13
5		1		5		10
				5
			а	2			б
			а				б

K0		1		1		4	(7)	1		x1	x2	x3		1	1
	е1	2	(1)	2				2		x1	x2	x3
		2		2	е2			2	е3	e0				0	2
4		3	(2)	3	е2			3	е3	e0			H=	0	2
													H=	3	3


		(3)			(4)										4
					(4)		(6)							1



(5)				1							x4
				2	е4	3			e0	а			б		в
				2	е4

		3	2	1	4
	3		d32	d31	d34
	3	0	d32	d31	d34
Dr=	2	d24	0	d21	d24
Dr=	1	d31	d24	0	d14
	1	d31	d24	0	d14
	4	d43	d42	d41	0

	1	2	3	4	5	6	7	8	9	10	11
1
1		2	1	2	3	1	2	3	1

2	2	1	3	1	2	3	1	2	2

3	1	3	2	3	1	2	3	1	3

4	3	2	1	2	3	1	2	3

5	2	1	А	1	2		3	1

6	3	2	1	2	3		1	2
7	1	3	2	3	1		2	3
8	2	1	3	1	2		3	1	В
9
9	3	2	1	2	3	1	2	3
10
10	1	3	2	3	1	2

				3
1	&	9	&	1			12
1		9					12
				4
2	3	10	8	4
2		10			1		11
					1

4	&	1	&	5
	&		&
	6		1				1
	6		1	1			1
5		1				10	13
5		1		5		10
				5
			а	2			б
			а				б

K0		1		1		4	(7)	1		x1	x2	x3		1	1
	е1	2	(1)	2				2		x1	x2	x3
		2		2	е2			2	е3	e0				0	2
4		3	(2)	3	е2			3	е3	e0			H=	0	2
													H=	3	3


		(3)			(4)										4
					(4)		(6)							1



(5)				1							x4
				2	е4	3			e0	а			б		в
				2	е4

		3	2	1	4
	3		d32	d31	d34
	3	0	d32	d31	d34
Dr=	2	d24	0	d21	d24
Dr=	1	d31	d24	0	d14
	1	d31	d24	0	d14
	4	d43	d42	d41	0

	1	2	3	4	5	6	7	8	9	10	11
1
1		2	1	2	3	1	2	3	1

2	2	1	3	1	2	3	1	2	2

3	1	3	2	3	1	2	3	1	3

4	3	2	1	2	3	1	2	3

5	2	1	А	1	2		3	1

6	3	2	1	2	3		1	2
7	1	3	2	3	1		2	3
8	2	1	3	1	2		3	1	В
9
9	3	2	1	2	3	1	2	3
10
10	1	3	2	3	1	2

				3
1	&	9	&	1			12
1		9					12
				4
2	3	10	8	4
2		10			1		11
					1

4	&	1	&	5
	&		&
	6		1				1
	6		1	1			1
5		1				10	13
5		1		5		10
				5
			а	2			б
			а				б

K0		1		1		4	(7)	1		x1	x2	x3		1	1
	е1	2	(1)	2				2		x1	x2	x3
		2		2	е2			2	е3	e0				0	2
4		3	(2)	3	е2			3	е3	e0			H=	0	2
													H=	3	3


		(3)			(4)										4
					(4)		(6)							1



(5)				1							x4
				2	е4	3			e0	а			б		в
				2	е4

		3	2	1	4
	3		d32	d31	d34
	3	0	d32	d31	d34
Dr=	2	d24	0	d21	d24
Dr=	1	d31	d24	0	d14
	1	d31	d24	0	d14
	4	d43	d42	d41	0

	1	2	3	4	5	6	7	8	9	10	11
1
1		2	1	2	3	1	2	3	1

2	2	1	3	1	2	3	1	2	2

3	1	3	2	3	1	2	3	1	3

4	3	2	1	2	3	1	2	3

5	2	1	А	1	2		3	1

6	3	2	1	2	3		1	2
7	1	3	2	3	1		2	3
8	2	1	3	1	2		3	1	В
9
9	3	2	1	2	3	1	2	3
10
10	1	3	2	3	1	2