
- •Оглавление
- •ВВЕДЕНИЕ
- •1.8. Настройка программ-трассировщиков
- •2. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РАЗМЕЩЕНИЮ ЭРЭ И ЭЛЕМЕНТОВ ПЕЧАТНОГО МОНТАЖА
- •3. ОЦЕНКА КАЧЕСТВА РАЗРАБОТКИ
- •4. ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИРОВАННОГО ТОПОЛОГИЧЕСКОГО ПРОЕКТИРОВАНИЯ ПЕЧАТНЫХ ПЛАТ
- •4.2. Элементы теории множеств
- •4.5. Математические модели схем
- •4.6. Математические модели монтажного пространства
- •5. МЕТОДИКА ПРОЕКТИРОВАНИЯ ПЕЧАТНОГО МОНТАЖА
- •ПРИЛОЖЕНИЯ
- •Приложение 3
- •СПИСОК ЛИТЕРАТУРЫ

4. ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИРОВАННОГО ТОПОЛОГИЧЕСКОГО ПРОЕКТИРОВАНИЯ ПЕЧАТНЫХ ПЛАТ
4.1. Требования кматематическим моделям
Возможность правильной постановки задач топологического проектирования печатных плат и качество их решения в значительной степени зависит от математических моделей схемы, реализуемой на печатной плате и моделей монтажного пространства. В общем случае к перечисленным матема-
тическим моделям предъявляют следующие требования:
1.Информационная полнота, т. е. полнота отображения свойств объекта, необходимых для решения задач топологического проектирования.
2.Высокая степень формализации.
3.Наличие математического аппарата, позволяющего выполнять формальные преобразования.
4.Простота перехода от модели к объекту и обратно.
5.Возможность использования моделей в существующих алгоритмах.
6.Наглядность в представлении объекта.
7.Адекватность модели.
Всем перечисленным выше требованиям к математическим моделям в наибольшей степени удовлетворяет граф [13, 41, 43]. Геометрическое задание графа наглядно представляет отображаемый объект, а матричный и аналитический способы – формально. Графы и операции над ними в задачах топологического проектирования РЭС являются элементами теории множеств [41].
4.2. Элементы теории множеств
Множество – это совокупность объектов любой природы, называемых элементами данного множества, обладающих какими-либо общими для данного множества свойствами. Как основное понятие теории понятие множества не подлежит логическому определению [41].
Элементы множества могут иметь различную природу, например множество ЭРЭ, входящих в схему, или множество микросхем входящих в конструкцию. Множества обозначают заглавными буквами латинского алфавита, а элементы – строчными буквами с индексами.
В теории множеств применяют специальные символы и их сочетания, при помощи которых выражают определенные операции. На рис. 4.1 приведены наиболее часто применяемые символы [13, 41].
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-94- |

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.2.Элементы теории множеств
– объединение множеств |
– эквивалентность |
– пустое множество |
∩ – пересечение множеств |
– принадлежащий множеству |
→ – стремление |
–непринадлежащиймножеству |
Π – декартово произведение |
≠ – несоответствие |
– включение во множество |
= – соответствие (совпадение) |
– невключение во множество |
\ – разность множеств |
– отрицание |
– входящий во множество |
– каждый элемент множества |
– не входящий во множество |
– не каждый элемент множества |
– что |
– найдется такой элемент множества |
– соответствует |
- не найдется такой элемент множества |
: – такой, что |
выражение – наибольшее целое число |
Рис. 4.1. Набор наиболее часто используемых символов
Множество можно задать описательно: С = x X: x – транзистор . Запись означает, что во всем множестве X –ЭРЭ есть некоторое множество С-транзисторов. Читается запись как “множество С состоит из элементов x множества X, обладающих таким свойством, что x является транзистором”.
Рассмотрим также некоторые основные понятия теории множества.
Мощность множества
X = x j j =1, n , n – мощность множества.
Если n – определено то множество конечное, если не определено, то бесконечное.
Строка
В отличие от обычного множества, где порядок безразличен, в строке должен быть указан порядок элементов, например:
C = C5, C2, C1, C3, C4 .
Равенство множеств
X=Y – множество X равно множеству Y, если оба множества состоят из одних элементов.
Если множество X входит в множество Y и при этом Χ ≤ Υ, то говорят что X является подмножеством Y:
Y: X Y.
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-95- |
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.2.Элементы теории множеств
Если Χ ≤ Υ и Y≤X , то X =Y. Если X ≠Y, то множество X не совпадает с множеством Y.
|
|
|
|
|
|
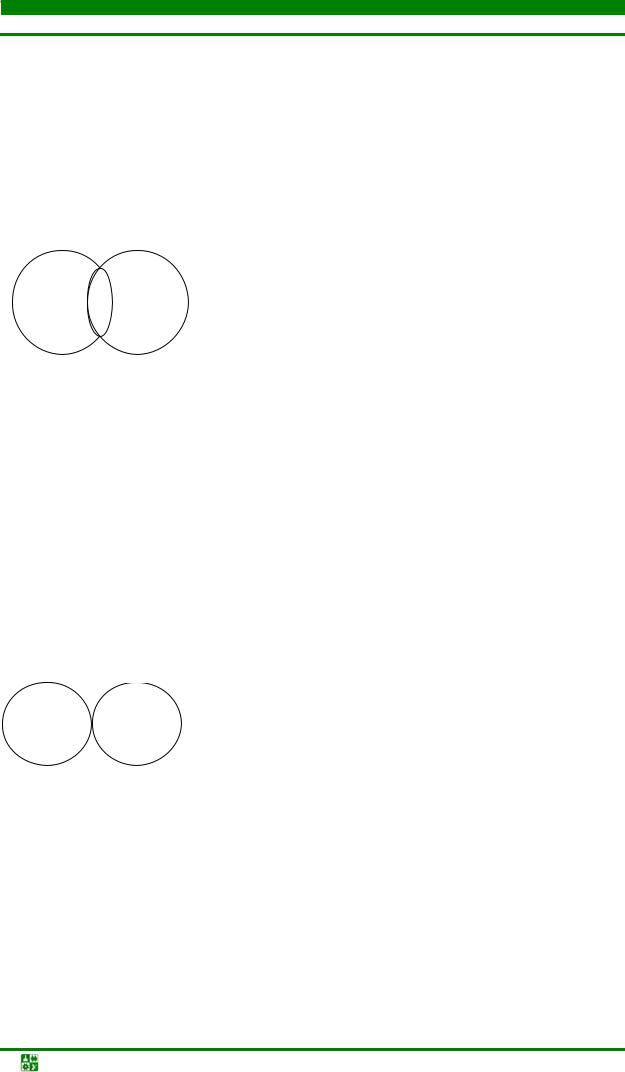
Пересечение множеств |
|
|
|
|
|
Множество P является результатом пересечений множеств |
X |
и Y |
|||||||
(рис. 4.2): |
|
|
|
|
P= X ∩ Y. |
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
P |
|
В качестве примера можно привести |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
множество |
P (общее |
число |
меж- |
|
|
|
|
|
|
|
платных соединений) для плат X и Y. |
||||
|
X |
|
|
|
Y |
|||||
|
|
|
|
Если рассматривается |
пересечение не- |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
скольких |
множеств, |
например |
X1, |
|
|
|
|
|
|
|
X2,…, Xn , то в этом случае запись |
вы- |
|||
|
|
|
|
|
|
глядит следующим образом: |
|
|
||
Рис. 4.2. Пересечение множеств
n
P = ∩ Xi , i = 1
Для пересекающихся множеств справедлив переместительный закон,
т. е. P=X ∩ Y = Y∩ X.
Объединение множеств
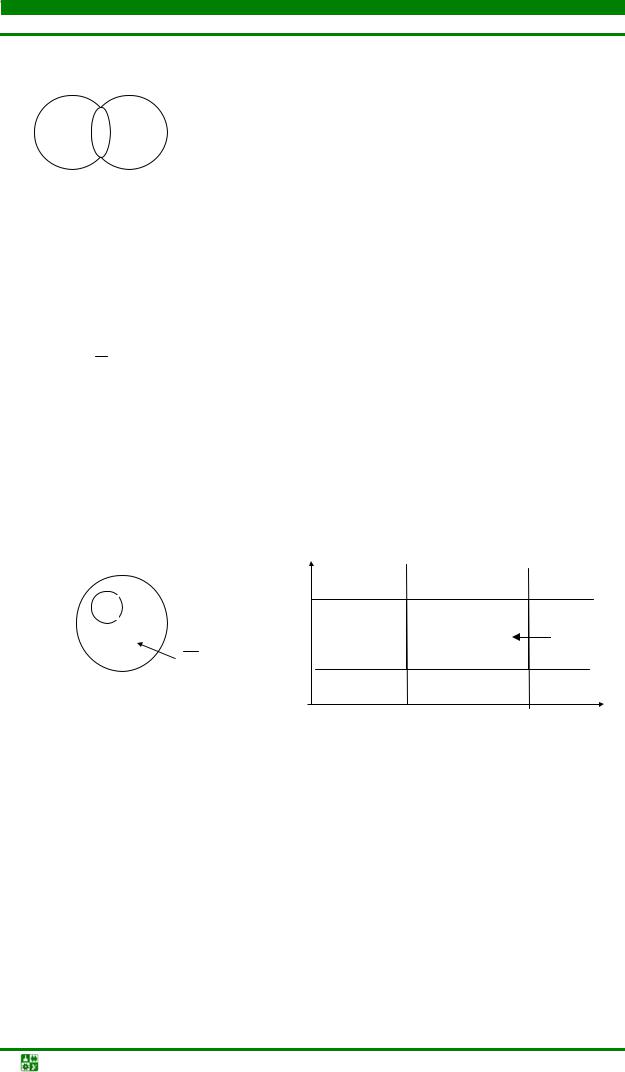
Объединение множеств X и Y приводит к образованию нового множества L, которое получается из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств X или Y (рис. 4.3).
Запись операции объединения выглядит как
X Y
L (заштриховано)
Рис. 4.3. Объединение множеств
L= X Y.
Множество L может, например, отражать число типоразмеров плат X и Y. Множество L может получиться в результате объединения нескольких
множеств: |
n |
|
||
L = |
Xi . |
|||
|
1 |
|||
|
i = |
|
||
Для операции объединения множеств так же как и для операции пересечения множеств, справедлив переместительный закон.
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-96- |
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.2.Элементы теории множеств
X Y
R
Рис. 4.4. Разность множеств
Разность множеств
Разность множеств X и Y есть новое множество R (рис. 4.4), которое образуется из элементов X, за исключением элементов, принадлежащих X и Y одновременно:
R = X \ Y.
В качестве множества R может выступать, например, число типоразмеров, принадлежащих только одной печатной плате.
Дополнение множества
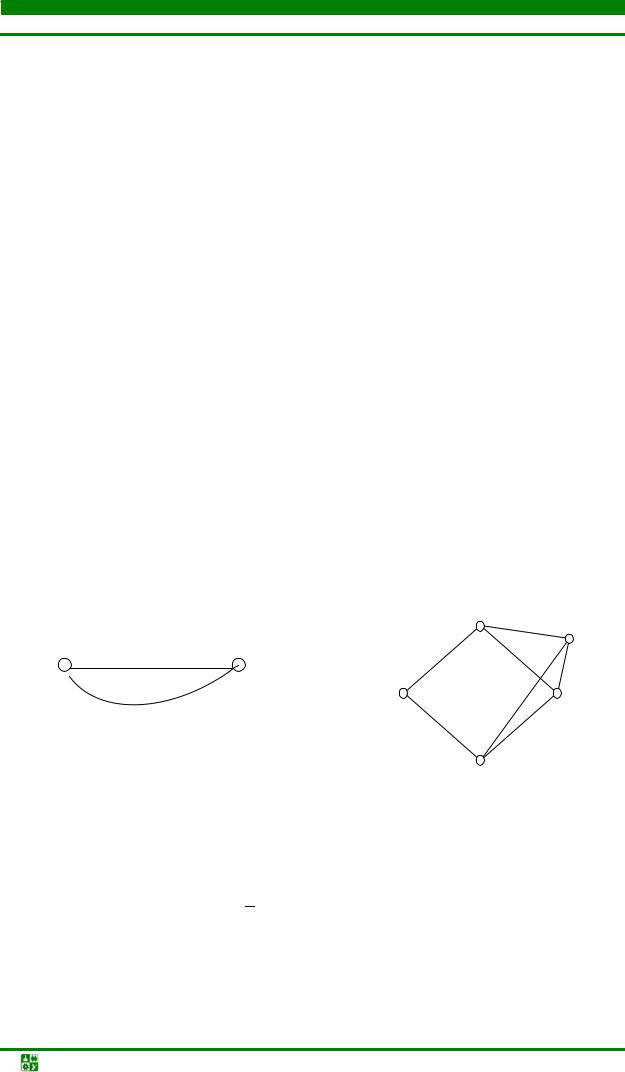
Дополнением множества X по отношению к множеству Y называют
множество X , состоящее из элементов множества Y не принадлежащих множеству X (рис. 4.5).
Произведение множеств
Декартово произведение множеств X и Y есть множество Z упорядоченных пар (X,Y), образованных множествами X и Y (рис. 4.6):
Z = X1 • Y1.
|
|
Y |
X |
Y |
|
|
|
|
|
Y1 |
Z |
|
X |
|
|
|
|
|
|
X |
|
|
X1 |
Рис. 4.5. Дополнение множества |
Рис. 4.6. Декартово произведение |
|
множеств |
Разбиение множеств
Разбиением множества X называют такое множество множеств X j , где j J, а J – некоторое множество индексов j, при котором выполняются следующие условия:
1.Xj X при всех j J.
2.Xj ≠ .
3. Xj ∩ Xi ≠ при i ≠ j.
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-97- |

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.2.Элементы теории множеств
4. Xj= X.
j J
В качестве примера можно привести операцию разбиения множества конструктивных узлов РЭС более высокого уровня иерархии на конструктивные узлы более низкого иерархического уровня.
Универсальное множество
Понятие пустого множества в теории множеств аналогично нулю в алгебре чисел, т. е.
α • = и α + = α,
где α – число.
Для любого множества справедливо: X ∩ = и X =X. Введем понятие множества I, соответствующее единице, т. е. α • 1= α,
а для пересекающихся множеств: X ∩ I = X, где I называют универсальным или единичным множеством. В ряде случаев в качестве I могут использоваться различные общие подмножества, т. е. рассматриваются подмножества некоторого фиксированного множества I, при этом множество I является самым большим и универсальным.
Пример 1. Среди множества комплектов конструкторских документов на изготовление РЭС полный комплект документов является универ-
сальным множеством.
Пример 2. При рассмотрении множества микрокорпусных элементов отдельных печатных узлов РЭС выделяют универсальное множество мик-
рокорпусных элементов, входящих во все РЭС в целом. Универсальное множество обладает свойством, не имеющим аналога в алгебре чисел, а именно для любого множества X справедливо:
X I = I.
То есть в I должны входить все элементы множества X и дополняющие элементы множества I. Но при этом все элементы X входят в I, поэтому их объединение равно I.
В связи с вышеизложенными выводами легко определить дополнение множества X как
X = I / X.
Двойное дополнение X = X .
При помощи операции дополнения можно в удобном виде представить разность множеств:
X \ Y = x: x X и X Y = x: x X и x Y =X ∩ Y .
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-98- |

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.2.Элементы теории множеств
Определения в теории множеств
В теории множеств принято некоторые определения записывать в виде математических выражений с применением логических символов, например:
свойство транзитивности записывается как
X Y и Y Z X Z;
квантор общности: x (P(x) Q (x)) – все объекты обладающие свойством P(x) обладают и свойствами Q(x);
квантор существования: x (P(x) ∩ Q (x)) – существует по крайней мере один объект обладающий свойством P(x) и Q(x), т. е.
P(x) ∩ Q (x) ≠.
Отношение множеств
Элементы множества, как правило, находятся в каком-либо отношении друг относительно друга. Эти отношения можно задать в виде нескольких предложений (“меньше чем.......”, “больше, чем..........”, “эквивалентно.....” и т. д.). Тот факт что элемент Xi X находится в каком-либо отношении Xj X записывается как:
Xi R Xj,
где R – символ отношения.
Отношения из двух элементов множества X называют бинарным. Бинарное отношение множеств X и Y представляет собой некоторое множество упорядоченных пар (x, y) образованных декартовым произведением X и Y. Рассмотрим основные виды отношений.
Эквивалентность
Некоторые элементы множества можно считать эквивалентными в том случае, когда любой из этих элементов при определенных условиях можно заменить другим, т. е. данные элементы находятся в отношении эквивалентности. В качестве примера можно привести принадлежность транзистора к одной группе, выделенной по однотипному варианту установки на печатной плате.
В общем случае можно определить следующие условия эквивалентности:
1.X ~X –рефлективность (каждый элемент эквивалентен самому себе).
2.X ~Y Y~X – симметричность.
3.X ~Y и Y~Z X ~Z – транзитивность (два элемента эквивалентны третьему, эквивалентны между собой).
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-99- |

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.2.Элементы теории множеств
Следовательно, отношение R называют отношением эквивалентности, если оно рефлективно, симметрично и транзитивно.
Пример. Пусть некоторому элементу x входящему во множество X, эквивалентно подмножество А X, тогда это подмножество А образует класс эквивалентности x. Очевидно, что все элементы одного и того же класса эквивалентности обладают свойством транзитивности, т. е. эквивалентны между собой (свойство транзитивности). Тогда всякий элемент x X может находиться в одном и только одном классе эквивалентности, т. е. в этом случае множество X разбивается на некоторое непересекающееся подмножество классов эквивалентности
Aj X: j J ,
где J – некоторое множество индексов.
Таким образом, каждому отношению эквивалентности на множестве X соответствует некоторое разбиение множества X на классы Aj.
В ряде случаев в процессе разработки РЭС сталкиваются с отношениями, которые определяют некоторый порядок расположения элементов множества, например процесс ввода данных в алгоритмах. Одни данные вводятся раньше, а другие – позже во всем множестве данных. При этом может оказаться, что элементы одного множества больше или меньше элементов другого множества и т. д. Во всех случаях можно расположить элементы множества X или группы элементов по убыванию или по возрастанию, т. е. можно ввести отношения порядка на множестве X..
Различают отношения строгого порядка <, , и т. д. и отношения нестрогого порядка , ≤ и. т. д. (см. рис. 4.1) Перечисленные отношения характеризуются следующими свойствами.
Для отношений строгого порядка:
1.X < X – ложно (антирефлексорность).
2.X < Y и Y < X – взаимоисключение (антисимметричность).
3.X< Y и Y < Z X < Z – транзитивность.
Для отношений нестрогого порядка: 1. X ≤ X – истинно (рефлексивность).
2. X ≤ Y ≤ X X=Y – антисимметричность. 3. X ≤ Y и Y ≤ Z X<Z – транзитивность.
Множество X упорядоченное, если любые его два элемента Xj и Xi сравнимы, т. е. Xi < Xj, Xi = Xj или Xi > Xj. Упорядоченное множество называют кортежем. Элементы такого множества называют компонентами кортежа, которые занимают вполне определенное место в последовательности элементов и не могут произвольно ставиться в другое место. Например, числовая последовательность прогрессии или технологический процесс сборки РЭС.
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-100- |

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.2.Элементы теории множеств
При обработке конструкторской документации на компьютере часто используют отношения доминирования. При этом говорят, что X X доминирует над y X, т. е. x >> y, если элемент x в чем-либо имеет приоритет над y. Например: X – список данных, который поступает первый на обработку. Свойство транзитивности в этом случае не имеет смысла. Например, если вариант конструкции РЭС “X” предпочтителен по каким-либо параметрам над вариантом конструкции “Y”, а “Y” по каким-либо параметрам предпочтителен над “Z”, то отсюда не следует что варианту конструкции “X” должно быть отдано предпочтение над вариантом “Z”.
|
|
|
|
Отображение множеств |
|
Если заданы |
два непустых множества X и Y, то закон, по которому |
||||
каждому элементу x X ставится в соответствие |
элемент Гx Y, называют |
||||
однозначным |
отображением X в Y или функцией, определенной на X и |
||||
принимающей значение на Y . |
|
||||
На практике приходится иметь дело с многозначными отображе- |
|||||
ниями |
множества |
X на Y, определяющими закон, согласно которому каж- |
|||
дому |
элементу x X ставится в соответствие |
некоторое подмножество |
|||
Гx Y, называемое образом элемента x. Возможны случаи, когда Гx= . |
|||||
Пусть |
задано |
некоторое подмножество |
A Y. Для любого x А |
||
образом x является |
подмножество Гx Y. Совокупность всех элементов |
||||
Y, являющихся образами для всех x А, назовем образом множества А и
будем обозначать |
ГА. |
При этом |
ГА будет |
представлять |
собой выраже- |
||||
ние |
|
ГА |
= |
|
|
Гx . |
|
||
|
|
|
|
|
|||||
|
|
|
|
x A |
|
|
|
||
Операция отображения обладает рядом свойств. Рассмотрим наибо- |
|||||||||
лее важные из них. |
|
|
|
A1 X и |
A2 X, то |
|
|||
Если заданы два |
подмножества |
для отображе- |
|||||||
ния объединения этих подмножеств |
|
|
|
|
|
||||
ГА( А А2) = |
|
Гx = ( |
|
|
Гx ) ( |
Гx ) = ГА1 ГА 2 |
|||
x A1 A2 |
x A1 |
|
x A2 |
|
|||||
При отображении пересечений |
рассмотренных выше |
подмножеств |
|||||||
Г(A1 ∩ A2) соотношение Г(A1 ∩ A2)=ГА1 |
∩ ГА2 |
справедливо только в том |
|||||||
случае, когда отображение является |
однозначным. В общем случае мо- |
||||||||
жет быть применено выражение Г(A1 ∩ A2 ) ГА1 ∩ ГА2. |
Произведением |
||||||||
Пусть Г и |
О |
- отображения |
множества X в X. |
||||||
(композицией) этих |
отображений |
назовем |
отображение ГО, которое со- |
||||||
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-101- |
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.2.Элементы теории множеств
гласно свойству ассоциативности композиции определим следующим об-
разом: (ГО)x = Г (Оx).
Для многократного отображения множества X в X, когда Г=О,
Г2x = Г (Гx); Г3x=Г(Г2x)=Г(Г(Гx)) и т. д., ГГ-1x=x,
где Г-1x – обратное отображение.
4.3. Основныепонятиятеорииграфов
Граф G(X, U) представляет собой совокупность непустого множества X (вершин) и изолированного от X множества U (дуг или ребер), представляющего собой множество всех упорядоченных пар (Xi Xj), xi, xj X
(рис. 4.7).
Можно дать более точное определение графа [42]. Граф G(X, U, F) - совокупность трех объектов: множества вершин X, множества ребер U и инцидентора F, указывающего, какие пары вершин с какими ребрами соединены.
Вершины Xi и Xj, которым соответствует некоторое ребро Uk, называют смежными или инцидентными ребру Uk (рис. 4.7). Два ребра также считаются смежными, если они имеют общую вершину (см. рис. 4.7).
Ниже дадим основные понятия теории графов [42].
Если порядок вершин в паре Xi, Xj безразличен, то ребро называют звеном, в противном случае –дугой. Несколько однотипных ребер (звеньев, дуг) между одной парой вершин считают параллельными.
|
|
X4 |
U3 |
X5 |
|
|
|
||
|
U1 |
U2 |
U |
U |
X1 |
X2 |
X1 |
5 |
7 |
|
|
|
X3 |
|
|
|
|
|
U2 |
U |
1 |
|
U6 |
|
|
|||
|
|
|
||
Рис. 4.7. Фрагмент графа |
|
|
|
|
|
|
|
|
|
|
|
|
X2 |
|
|
|
|
|
|
|
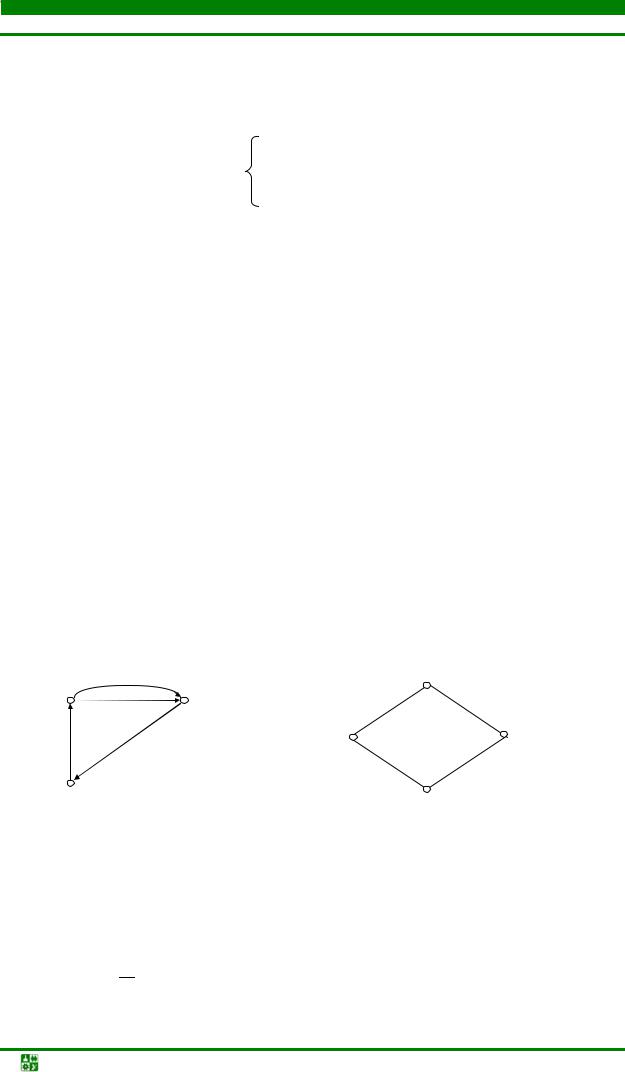
Рис. 4.8. Пример неографа |
|||
Неориентированный граф (неограф) – граф, все ребра которого являются звеньями (см. рис. 4.8).
Ориентированный граф (орграф) – граф, у которого все ребра дуги
(см. рис. 4.9).
Аналитически можно описать любой ориентированный граф системой уравнений [41], связывающих параметры xi X, и наоборот, любая сис-
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-102- |
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.3.Основные понятия теории графов
тема алгебраических уравнений может быть представлена в виде направленного графа. Например, граф, приведенный на рис. 4.9, определяет следующую систему уравнений:
X1=T31 X3;
X2=T12 X1;
X3=2T23 X2,
где Тij – отношение элемента Xi к элементу Xj.
Задание графов через операцию отображения множеств. Отдельным способом задания неографов и орграфов может служить операция ото-
бражения множеств. Граф задан, если задано непустое множество X и
отображение Г множества X в X. Если обозначить такой граф как G(X, Г), то при его геометрической интерпретации каждую вершину xi X соединяют со всеми вершинами xj Гxi. Например, для графа G(X, Г), приведенного на рис. 4.8, можно записать Х={X1, X2, X3, X4 , X5}; ГX1={ X2, X4};
ГX2={ X1, X5, X3}; ГX3={ X2, X4, X5}; ГX4={ X1, X3, X5}; ГX5={ X4, X2, X3}.
Смешанный граф – граф, у которого имеются как звенья, так и дуги.
Ориентация графа – замена звена дугой или двумя разнонаправленными дугами.
Дезориентация графа – замена дуг звеньями.
Список смежности S(Xi) вершины Xi X- множество смежных с ней
вершин. Например, для вершин X3 и X5 (см. рис. 4.8): S (X3) = X2, X4, X5 ,
S(X5) = X4, X3, X2 .
|
U22 |
|
1 |
|
|
|
|
X2 |
U21 |
X3 |
|
|
|
4 |
2 |
|
X1 |
|
3 |
Рис. 4.9. Пример орграфа |
Рис. 4.10. Пример униграфа |
||
Неограф удобно описывать списком смежности всех его вершин:
G = ( x, S(x) ).
Степенью вершины Xi считают длину S(Xi) его списка смежности.
Униграф – граф, у которого каждой паре вершин соответствует не более одного ребра (рис. 4.10), такой граф можно задавать, представляя каж-
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-103- |
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.3.Основные понятия теории графов
дое ребро как пару соответствующих вершин: Uk = (Xi, Xj). Для орграфа: Xi – начало дуги, а Xj – конец дуги.
Мультграф – граф, у которого имеется хотя бы одна пара вершин, которой соответствует несколько ребер (см. рис. 4.8).
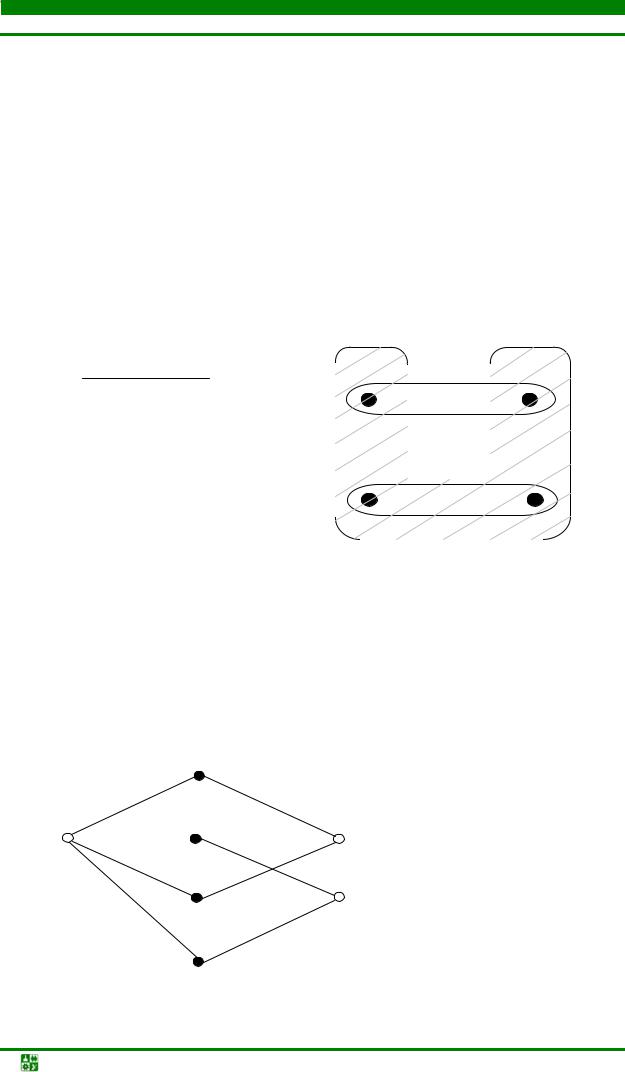
Гиперграф G=(E, C) – совокупность двух множеств E и C, представ-
ляющих, |
например, элементы и цепи схемы электрической принципиальной. |
|
Цепь с |
|
С – есть некоторое подмножество элементов множества Е. Это по- |
|
||
нятие является обобщением неориентированного графа, любое ребро которого является подмножеством из двух элементов, принадлежащих Е. Графически ребро гиперграфа изображается односвязной областью, внутри которой находятся соответствующие точки первого множества. Для схемы, изображенной на рис. 4.11 гиперграф приведен на рис. 4.12.
.
|
|
C1 |
|
|
|
|
|
X |
|
X3 |
||
|
|
|
|
|
|
|
|
|||||
|
X1 |
|
X3 |
|
|
|
C1 |
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
C2 |
|
|
|
|
|
|
X4 |
||
|
|
|
|
|
|
|
|
|
X2 |
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||
|
X2 |
C |
3 |
|
X4 |
|
|
|
C |
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
Х={X1, X2, X3, X4} – элементы |
|
|
|
|||||||||
|
Рис. 4.12. Гиперграф схемы |
|||||||||||
|
С={C1, C2, C3} - цепи |
|
||||||||||
|
|
|
|
|
|
|
||||||
|
Рис. 4.11. Схема соединений |
|
|
|
|
|
|
|||||
|
|
элементов Х1 …Х4 |
|
|
|
|
|
|
|
|
||
Двудольный граф. Граф G=(Z, Y) называется двудольным, если множество его вершин можно разбить на два непересекающихся подмножества так, чтобы вершины одного и того же подмножества не были смежны.
Пример. Двудольный граф схемы, приведенный на рис. 4.11, имеет вид, представленный на рис. 4.13.
|
X1 |
|
|
С2 |
X2 |
Z=X U C |
|
|
С1 |
Y={(C1, X1), |
|
|
|||
|
|
||
|
X3 |
(C1, X3),...,(C2, X4)} |
|
|
|
||
|
|
С3 |
|
x 4
Рис. 4.13. Двудольный граф схемы
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-104- |
4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.3.Основные понятия теории графов
Путь ρ(V0,Vk) на графе G – это последовательность попарно смежных ребер, первое из которых инцидентно вершине V0, а последнее - Vk.
Цикл – замкнутый путь.
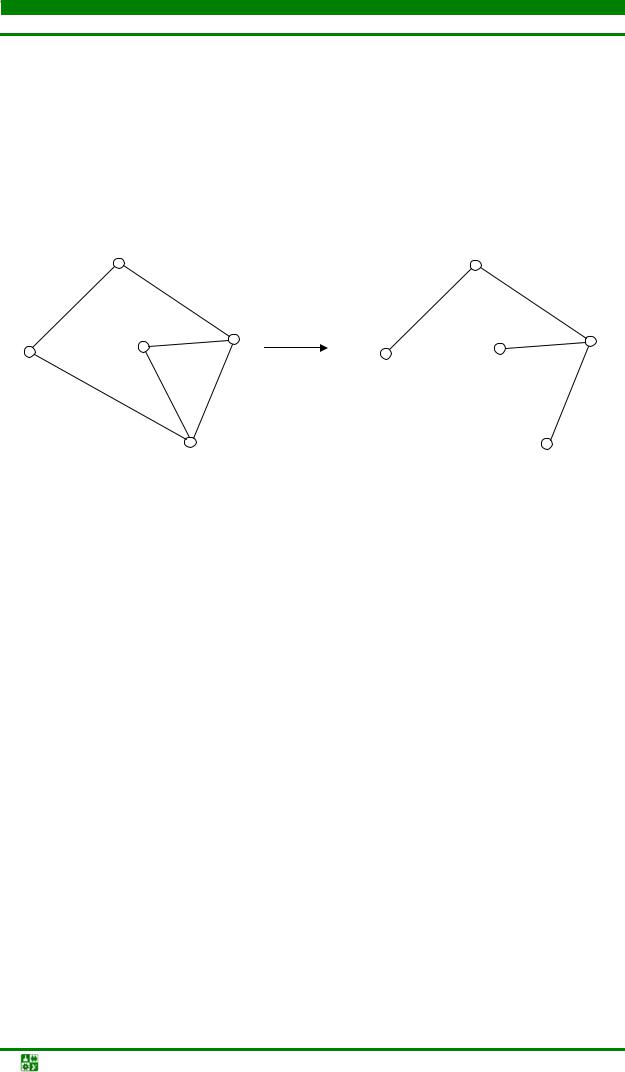
Дерево – связный граф без циклов (рис. 4.14). Граф G связен, если для любых его вершин существует связывающий их путь. Граф G несвязен, если для некоторой пары вершин не существует связывающего их пути.
2 |
Граф |
Дерево графа |
2 |
|
|
|
5 |
|
5 |
1 |
4 |
1 |
4 |
|
|
3 |
3 |
Рис. 4.14. Пример построения дерева графа
Эйлеров цикл – граф, в котором может быть построен цикл, начинающийся из вершины i и заканчивающийся в вершине i, проходящий по каждому ребру не более одного раза. Граф может быть Эйлеров если:
1)является связным;
2)если степень каждой вершины графа четная.
Гамильтонов цикл - существующий в графе цикл, позволяющий пройти все вершины графа не более одного раза.
4.4. Общаяпостановказадачтопологическогопроектирования
Как отмечалось, в параграфе 1.3 к задачам топологического проектирования РЭС в целом относят такие основные процедуры, как компоновка, размещение и трассировка. При топологическом проектировании печатных плат, как правило, используют две последние процедуры. Однако при изложении материала будем рассматривать в общем виде и процедуру компоновки, так как ее выполнение в итеративном цикле может быть связано с остальными процедурами топологического проектирования ПП.
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-105- |

4.ОСНОВЫ МАТЕМ-ГО ОБЕСПЕЧЕНИЯ АВТОМАТИЗИР-ГО ТОПОЛОГИЧЕСКОГО ПРОЕКТ-Я ПЕЧАТНЫХ ПЛАТ
4.4.Общая постановка задач топологического проектирования
Общая постановка задачи компоновки
Задача компоновки, в общем виде, заключается в распределении элементов схемы (в общем случае – модулей предыдущего уровня иерархии) по монтажным пространствам несущих элементов (в общем случае – по монтажным пространствам несущих элементов данного уровня иерархии). При этом в качестве несущих элементов могут выступать, например, печатные платы, подложки микросборок, кристаллы БИС и т. п. При решении задачи компоновки основным критерием оптимальности является минимизация числа межмодульных связей (разъемных соединений на несущих элементах или числа выводов стандартных корпусов БИС).
В процессе проектирования РЭС выделяют два варианта постановки задачи компоновки [13]:
1.Компоновка схем в типовые конструкции, не имеющие схемной унификации, например разрезание электрической принципиальной схемы устройства на части заданного размера (например на типовые элементы замены).
2.Компоновка схем в модули заданного схемно-унифицированного набора (называют покрытием), например переход от схемы электрической функциональной к схеме электрической принципиальной, реализованной на наборе интегральных схем (ИС), больших ИС и сверхбольших ИС.
Общая постановка задачи размещения
В общем виде задача размещения [13] заключается в определении оптимального в смысле некоторого критерия положения элементов и связей между ними в монтажном пространстве типовой конструкции РЭС. При этом должны соблюдаться конструктивно-технологические ограничения.
Для регулярного монтажного пространства (например для субблока или ПП, на которой предполагается устанавливать однотипные ЭРЭ) задачу размещения можно сформулировать следующим образом.
Имеется множество элементов E={li / i=1, N} и множество соединяющих их цепей Q={qk/ k=1, K}. Монтажное пространство определено множеством фиксированных позиций для установки элементов T={tj / j=1, M}, причём М ≥ N. Необходимо найти такое отображение множеств Е на множестве Т, при котором достигается экстремум целевой функции F.
Главной целью размещения является создание наилучших условий для последующей трассировки.
Общая постановка задачи трассировки
Трассировка [13] заключается в определении конкретных геометрических параметров печатного, плёночного или проводного монтажа, реализующего соединения между элементами схемы. При этом исходными данными являются: список цепей, метрические параметры и топологические свойства типовой конструкции и её элементов, результаты решения задачи раз-
Автоматизация проектирования РЭС. Топологическое проектирование печатных плат. Учебное пособие |
-106- |
