Шпоры по физике 3 семестр 2 поток / 40

40. Энергия магнитного поля. Плотность энергии.

Рассмотрим цепь. При замкнутом ключе в соленоиде установится ток , который обусловит магнитное поле, сцепленное с витками соленоида. Если разомкнуть ключ, то через сопротивление будет некоторое время течь постепенно убывающий ток, поддерживаемый возникающей в соленоиде ЭДС самоиндукции.        При этом работа равна: . Если индуктивность соленоида не зависит от , то , тогда: . Проинтегрировав получим работу, совершаемую в цепи за все время, в течение которого происходит исчезновение магнитного поля: . Работа идет на приращение внутренней энергии сопротивления. Проводник с индуктивностью, по которому течет ток силы , обладает энергией: . Выражение для работы можно трактовать как работу, которую необходимо совершить против ЭДС самоиндукции равную: . C помощью преобразований получим: . Выразим энергию магнитного поля через величины, характеризующие само поле. В случае очень длинного соленоида , подставив эти значения в выражение для энергии получим: . Так как магнитное поле бесконечно длинного соленоида однородно и отлично от нуля только внутри соленоида, следовательно, энергия локализована внутри соленоида и распределена по его объему с постоянной плотностью ω. . . Зная плотность энергии поля в каждой точке, можно найти энергию поля в любом объеме V . В случае N связанных контуров получается выражение: , где 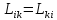– взаимная индуктивность -го и -го контуров, а – индуктивность -го контура.