|
27.
Поле в центре и на оси кругового
тока. Рассмотрим
поле, создаваемое током I,
текущим по тонкому проводу, имеющему
форму окружности радиуса R
.

Определим
магнитную индукцию на оси проводника
с током на расстоянии х
от плоскости кругового тока. Векторы
 перпендикулярны
плоскостям, проходящим через
соответствующие перпендикулярны
плоскостям, проходящим через
соответствующие
 и и
 .
Следовательно, они образуют симметричный
конический веер. Из соображения
симметрии видно, что результирующий
вектор .
Следовательно, они образуют симметричный
конический веер. Из соображения
симметрии видно, что результирующий
вектор
 направлен
вдоль оси кругового тока. Каждый из
векторов направлен
вдоль оси кругового тока. Каждый из
векторов
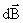 вносит
вклад равный вносит
вклад равный
 ,
а ,
а
 взаимно
уничтожаются. Но взаимно
уничтожаются. Но
 , ,
 ,
а т.к. угол между ,
а т.к. угол между
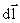 и и
 α
– прямой, то α
– прямой, то
 тогда
получим тогда
получим
 , ,
Подставив
в
 и,
проинтегрировав по всему контуру и,
проинтегрировав по всему контуру
 ,
получим выражение для нахождения
магнитной
индукции кругового
тока: ,
получим выражение для нахождения
магнитной
индукции кругового
тока:
 , ,
При
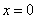 ,
получим магнитную
индукцию в центре кругового тока: ,
получим магнитную
индукцию в центре кругового тока:
 , ,
Заметим,
что в числителе
 –
магнитный момент контура. Тогда, на
большом расстоянии от контура, при –
магнитный момент контура. Тогда, на
большом расстоянии от контура, при
 ,
магнитную индукцию можно рассчитать
по формуле: ,
магнитную индукцию можно рассчитать
по формуле:
 , ,
|


