Шпоры по физике 3 семестр 2 поток / 1

1. Линии напряженности эл. поля и эквип. пов-ти. Связь между напр-ю и потенц-ом. Взаимодействие между покоящимися зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства - создает в нем электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку заряд оказывается под действием силы. Исследуем с помощью точечного пробного заряда qпр поле, создаваемое неподвижным точечным зарядом q, поместив в точку, положение которой относительно q определяется вектором . На пробный заряд действует сила . Отношение для всех пробных зарядов будет одним и тем же, поэтому примем это его в качестве характеристики электрического поля – напряженности . Опыт (Кулона) показывает, что сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми на данный заряд действует каждый из зарядов системы в отдельности. Отсюда вытекает принцип суперпозиции эл. полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядом с-мы в отдельности . Электрическое поле можно описать, указав для каждой точки модуль и направление вектора тих векторов создает образует поле вектора напряженности, которое можно также описать с помощью линий напряженности . Их проводят так, чтобы касательная к ним в каждой точке совпадала с направлением Густота линий выбирается так, чтобы число линий, пронизывающих единицу поверхности, перпендикулярную к линиям площадки, было равно модулю

Электрическое поле можно описать либо с помощью векторной величины – напряженности либо с помощью скалярной величины – потенциала . Между ними должна существовать связь, очевидно , напоминающая связь между силой и потенциальной энергией : ; ; вынося константу q за знак градиента и сократив его, получим . Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью, чье уравнение имеет вид . При перемещении по эквипотенциальной поверхности на отрезок потенциал не изменяется касательная к поверхности составляющая вектора равна нулю. 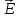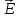Значит, вектор в каждой точке направлен по нормали к эквипотенциальной поверхности, проходящей через данную точку.