Шпоры по физике 3 семестр 2 поток / 5

5.Поле объемно-заряженного шара.Пусть шар радиуса R заряжен с постоянной объемной плотностью ρ. Поле в этом случае обладает центральной симметрией. Легко сообразить,что для поля вне шара получается тот же результат, что и в случае поверхностно-заряженной сферы: E( r ) = (r≥R).

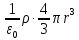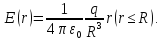Однако для точек внутри шара результат будет иным. Сферическая поверхность радиуса r (r < R) заключает в себе заряд, равный ρ*(4/3)π. Поэтому теорема Гаусса для такой поверхности запишется следующим образом: E(r) * 4π = . Отсюда, заменив ρ на q/((4/3)π, получим: Таким образом, внутри шара напряженность поля растет линейно с расстоянием r от центра шара. Вне шара напряженность убывает по такому же закону, как и у поля точечного заряда.