3. Системы единиц

1). СИ - общепринятая система единиц, мы будем работать в ней.

1 Кл =

Скорость света в СИ: с =

2). СГСЭ – абсолютная электростатическая система единиц.

В ее основе лежит

абсолютная электростатическая единица заряда – заряд, который взаимодействует с силой в 1 дину с таким же зарядом, находящимся на расстоянии 1 см.

e = 4,8ед. зар. СГСЭ

k = 1, т.о. закон Кулона в СГСЭ системе имеет вид

3). Гауссова система.

В Гауссовой системе единицы измерения

электрических величин - такие же, как в СГСЭ,

магнитных величин - как в СГСМ, в основе которой лежит закон взаимодействия между проводниками с током.

4. Принцип суперпозиции

1. Для дискретной системы зарядов:

;

2.Для непрерывно распределенного заряда

1) с объемной плотностью заряда :

- сила, действующая на зарядсо стороны объемно заряженного тела.

Здесь плотность заряда тела ,

суммарный заряд тела .

3) Для непрерывно распределенного заряда с поверхностной плотностью заряда

Суммарная сила.

4) Для непрерывно распределенного заряда с линейной плотностью заряда

, где.

5.Напряженность электрического поля

Все взаимодействия осуществляются через поля. Вспомним, каким может быть поле с точки зрения классификации:

1) однородное

2) центральное

3) стационарное

4) потенциальное поле:

5) консервативное потенциальное + стационарное

- сила, действующая на единичный точечный положительный заряд.

Электрическое поле можно описать, указав в любой точке пространства величину и направление . Совокупность этих векторов образует силовые линии поля.

Силовыми линиями являются линии, в каждой точке которых вектор является касательным к ним.

Густота силовых линий выбирается так, чтобы количество линий ,пронизывающих единицу площади поверхности, перпендикулярной к линиям, было равно числовому значению.

Для точечного заряда

Силовые линии электрического поля начинаются и кончаются на зарядах.

Если поле однородно, то линии поля эквидистантные.

7. Потенциал электростатического поля

Для точечного заряда:

поле центральное + стационарное =>поле консервативное

- потенциальная энергия единичного точечного положительного заряда, т.к. в консервативном поле для любого объекта существует функцияU, независящая от времени такая, чтосиле, действующей на этот объект,Uпри этом представляет собой потенциальную энергию этого объекта в данном консервативном поле.

Если взять в качестве объекта единичный точечный положительный заряд, то его потенциальная энергия будет представлять собой энергетическую характеристику данного электрического поля.

Потенциальную энергию единичного точечного положительного заряда называют потенциалом. Это скалярная величина .

Посмотрим, как определяется потенциал для системы с дискретным и непрерывным распределением заряда.

Для системы дискретных зарядов:

По аналогии с одним зарядом:

Найдем , сравнив полученный результат с формулой напряженности.

Вопр. По чему надо дифференцировать?

Отв.Поr, т.к., определяющая положение каждого заряда.

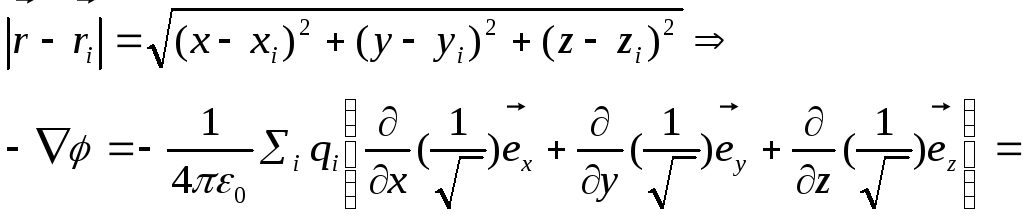
=ч.т.д.

Т.е. потенциал поля, создаваемого в данной точке системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности.

Если заряды распределены непрерывно, то

Потенциал определяется с точностью до const, поэтому его всегда можно нормировать удобным образом, задав.

Если конечный заряд распределить по конечной области пространства, то нормируют так:.

Поверхности, на которых =const, называют эквипотенциальными. Вектор напряженности эквипотенциальной поверхности в каждой ее точке, т.к производнаяпо любому направлению вдоль эквипотенциальной поверхности равна 0, следовательно, и соответствующая этой производной компонента напряженности поля

эквипотенциальной поверхности в каждой ее точке.