7. Сила, действующая на заряд, движущийся в

электромагнитном поле

Рассмотрим заряд , двигающийся со скоростьюв электромагнитном поле с напряженностьюи магнитной индукцией.

Сила, действующая на элемент тока

магнитная сила, действующая на движущийся в магнитном поле заряд.

Электрическая сила, действующая на заряд, определяется напряженностью электрического поля

Сила, действующая на заряд, движущийся в электромагнитном поле

- сила Лоренца.

Пример:

Рассмотрим 2 одинаковых по величине заряда , двигающихся параллельно друг другу с одинаковыми скоростями. Найдем силу взаимодействия зарядов

Магнитная индукция, создаваемая 2 зарядом в месте нахождения заряда 1, т.е. на перпендикуляре, проведенном к траектории движения заряда 2 из точки, в которой он в данной момент находится:

Найденное магнитное поле является полем движущегося заряда, оно и действует на заряд, летящий параллельно первому, с магнитной силой:

.

Опред.

-магнитное поле движущегося заряда.

Полученное соотношение справедливо и при релятивистских скоростях.

Если перейти в систему отсчета зарядов, то в ней магнитных сил не будет, и заряды будут взаимодействовать с электрической силой .

Вопр.Что же получается: в зависимости от того, из какой системы смотреть, изменяется сила? Ну а заряды как на это посмотрят? Они-то какую силу чувствуют? Может быть, мы сделали что-то не так?

Отв.Действительно, мы совершенно безосновательно считали, что электрическое поле

движущегося заряда . В нерелятивистском приближении полная сила, действующая на заряд в любой системе, должна быть одна и та же, но в системе, связанной с зарядом, она чисто электрическая, а в лабораторной системе она разделяется на электрическую и магнитную, следовательно, электрическое и магнитное поля переходят друг в друга, а так как заряды могут двигаться с высокими скоростями, то полная теория электромагнетизма должна быть релятивистской.

Электрические и магнитные поля при переходе из одной инерциальной системы в

другую преобразуются в соответствии с преобразованиями Лоренца (именно для этого Лоренц и написал свои преобразования, являющиеся краеугольным камнем Теории относительности).

Пусть движется относительносо скоростью, тогда при переходе в системукомпоненты электромагнитного поля преобразуются следующим образом:

;

;

;.

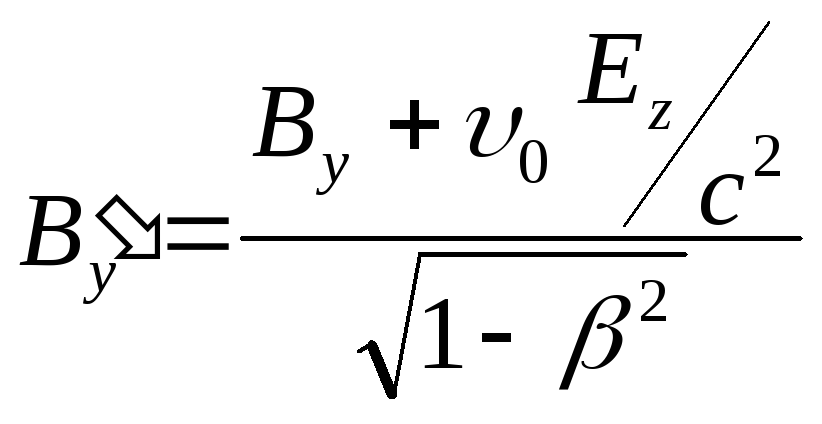Здесь .

Или разложив , где, имеем:

;

;

В нашем случае:

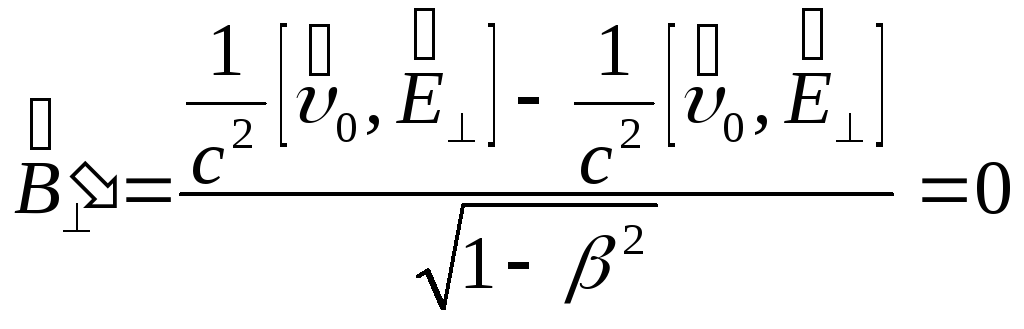;, то есть, в самом деле;

Т.о. в собственной системе заряды “чувствуют” меньшее электрическое поле, которое определяет собой такую же силу взаимодействия, как суммарная сила в лабораторной системе. Эта сила включает в себя нашу «лабораторную» электрическую силу и противодействующую ей «лабораторную» магнитную силу.

Выводы:

• справедливо и при релятивистских скоростях.

• Разделение силы на электрическую и магнитную условно и зависит от выбора системы отсчета.

8. Элементы векторного анализа. II часть

Продолжаем изучать свойства векторных полей. На очереди понятия:

циркуляция С и ротор.

1) Циркуляция

Пусть в любой точке пространства существует поле с напряженностью сила, действующая на единичный объект, равна.

- работа поля по перемещению единичного объекта на.

Если , то есть контур замкнутый, то - циркуляцияпо.

Физический смысл циркуляции: циркуляция - это работа сил поля по перемещению единичного объекта по замкнутому контуру.

Свойства циркуляции:

1. - алгебраическая скалярная величина.

2. зависит от направления обхода

3. Для консервативного поля сил .

Условие консервативности:

Именно потому, что электростатические поля консервативны, мы до сих пор не

использовали понятие циркуляции для нахождения распределения таких полей. Полезно иметь в виду, что условия равенства нулю являются, как правило, отрицающими или запрещающими, а не созидающими, т.к. по ним можно сказать только, чего нет и не может быть ( мы вернемся к этому вопросу, когда будем обсуждать смысл уравнений Максвелла).

Пример:

Векторное поле

Т.к. , то- неконсервативное поле.

4. Аддитивность

Циркуляция скорости - кинематическая характеристика течений жидкости или газа, которая служит мерой завихренности течения.

Если циркуляция скорости по любому замкнутому контуру, проведенному внутри

жидкости, равна нулю, то течение – безвихревое или потенциальное.

(Потенциальные скорости – однозначные функции координат).

Если , то существует вихри, которые, обтекая тело, приводят к существованию

силы, таково происхождение подъемной силы, в часности, крыла самолета, перпендикулярной к скорости :, где- плотность жидкости или газа.

Если, то- давление

2) Ротор== вихрь

Определение ротора:

Вихревое движение – это движение непрерывной среды, при котором перемещение её малых элементов состоит не только из поступательного движения, но и вращения около некоторой мгновенной оси.

Пример: смерчи, водовороты.

Если - поле скоростей частиц, то вихревая линия (линия, касательная к ротору) есть мгновенная ось вращения этих частиц.

Т.о. ротор определяет собой направление мгновенной оси вращения частицы, находящейся в данной точке.

Вихревые линии не могут начинаться и кончаться внутри однородной среды:

они или замкнуты или кончаются на границе раздела сред (поверхности Земли, жидкости, чашки, реки, ванны).

-такой вектор от данного, компоненты которого определяются циркуляцией данного вектора по трем ортогональным контурам.

- одно из обозначений.

Найдемдля декартовых координат из определения. В этом случае:

- что и требовалось доказать.

Аналогично:

Потенциальные (консервативные) поля являются безвихревыми,

т.к. для них все компоненты ротора равны 0 (.

Свойства :

1. - векторная функция векторного аргумента.

2. Аддитивность

3. нет завихрений в потенциальном поле.

Вопр.А как же смерчи на Земле?

Отв.Смерчи – следствие трения, также как воронки в ванне – следствие вязкости ,

в сверхтекучей жидкости турбулентности нет.

4. ,у вихрей нет источников.

5.

3) Теорема Стокса

Циркуляция по произвольному замкнутому контуруравна потокучерез произвольную поверхность, ограниченную данным контуром:

.