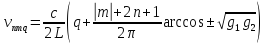гауссовы пучки / 13

13. Положение перетяжки в различных типах резонаторов. Собственные частоты.

А) Положение перетяжки.

Радиус кривизны Гауссова пучка , где .

Потребуем, чтобы на зеркалах резонатора радиус кривизны пучка совпадал с радиусом кривизны зеркала, тогда, с учетом правила знаков:

где - расстояние от перетяжки до соответствующего зеркала

Исключая , получим:

Кроме того, если - расстояние между зеркалами, то . Выразив отсюда , в итоге получим:

Этими формулами положение перетяжки задается однозначно. Приведем соответствующие значения для классических комбинаций:

Тип резонатора	Параметры
Конфокальный
Концентрический
Полуконфокальный
Полусферический

Б) Собственные частоты резонатора (прямоугольная и цилиндрическая симметрия).

Поле, образующееся в лазере, Наследует симметрию его элементов. Если апертура основного элемента, ограничивающего поле (в простейшем случае - зеркала с наименьшей апертурой, в более сложных резонаторах - например, диафрагма) имеет прямоугольную симметрию, то и поле будет иметь ту же симметрию. Если цилиндрическую, то и поле будет иметь цилиндрическую симметрию.

«Чистый» Гауссов пучок является приближенным решением волнового уравнения для поля в резонаторе в «основном состоянии» (если проводить аналогию с осциллятором в квантовой механике, которая, кстати говоря, имеет под собой все основания). Кроме основного, есть ещё и «возбужденные состояние», так называемые высшие моды. Высшие моды отличаются как по амплитудному, так и по фазовому составу. И амплитуда, и фаза поля зависят от симметрии.

В случае прямоугольной симметрии, выражение для высших мод запишется следующим образом (здесь и далее продольный амплитудный множитель опущен для краткости):

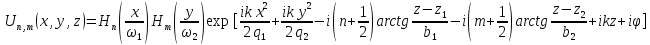
где , . - конфокальный параметр пучка. - полиномы Эрмита. Параметры определяют астигматизм пучка и могут иметь, в том числе, комплексные значения. Если , то в пучке отсутствует астигматизм. В дальнейшем будем рассматривать именно этот случай.

Индексы и характеризуют строение поля по осям и соответственно.

Выпишем фазу поля после полного прохода резонатора, опустив постоянную составляющую:

Величина сводится к где (не понял правда, как. это отражено в Быкове на стр. 22)

Чтобы в резонаторе образовывалась стоячая волна, необходимо, чтобы на зеркалах амплитуда обращалась в 0. Отсюда (q-целое):

откуда следует, что частота моды

В случае радиальной симметрии в выражении поля стоят не полиномы Эрмитта, а Лаггера, и выражение поля ещё более усложняется. Приведем лишь выражение для фазы на оси в этом случае (без постоянной составляющей):

Аналогичным образом отсюда вытекает выражение для собственных частот резонатора: