гауссовы пучки / 20_preobrazovanie_gaussovy_puchkov

ПРЕОБРАЗОВАНИЕ ГАУССОВЫХ ПУЧКОВ ТОНКОЙ ЛИНЗОЙ

Рассмотрим, что происходит с гауссовым пучком после прохождения идеальной тонкой линзы с фокусным расстоянием f установленным на расстоянии /₁ от перетяжки w₀₁ (рис. 1). Тонкая линза преобразует гауссов пучок с размером пятна в перетяжке w01 в пучок с размером пятна w₀₂, причем коэффициент преобразования а дается выражением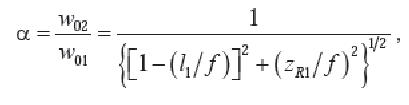

а местоположение перетяжки /₂ определяется соотношением

где

В этих формулах отношения /₁ / f и /₂ / f положительны, если линза собирающая, и отрицательны, если линза рассеивающая. Когда в результате расчета оказывается, что /₂ - отрицательно, пучок после линзы продолжает расходиться.

Если в (6) и (7) принять z_R << l₁ - f , то получим хорошо известные из геометрической оптики формулы для тонкой линзы

Рис. 1. Преобразование гауссова (а) и гомоцентрического (б) пучков тонкой линзой

Рассмотрим возможность преобразования гауссова пучка с размером пятна в перетяжке w01 в пучок с размером пятна в перетяжке w₀₂ с помощью тонкой линзы с фокусным расстоянием f. Для этого обратимся к формулам (6), (7) и проанализируем зависимость коэффициента преобразования a = w₀₁/ w₀₂ от величины /₁ / f. Эта зависимость приведена на рис. 2. Для некоторого конечного значения параметра z_R1 / f коэффициент преобразования с ростом l₁ / f сначала падает от начального значения

При /₁ / f = 1 коэффициент достигает минимума, равного (z_R1 / f) , а затем монотонно растет, стремясь к бесконечности при :

При варьировании величины от 1 до ∞ возможно достижение любого конфокального параметра преобразованного пучка, удовлетворяющего неравенству:

Это означает, что с помощью одной линзы не всегда удается получить перетяжку гауссова пучка заданного размера. Для этих целей часто используется двухлинзовая оптическая система.

3