гауссовы пучки / 19_selektsia_mod

1. Селекция поперечных мод диафрагмой

В большинстве случаев требуется выделить основную моду. Эта мода обладает наименьшими дифракционными потерями, ко­торые сильно нарастают при увеличении поперечного индекса мод. Но в устойчивых резонаторах дифракционные потери так малы, что различие между ними не может служить для дискриминации мод. Поэтому селекция может быть основана только на различиях в распределении поля мод с различными поперечными индексами. Так как основная мода имеет симметричное относительно оси резонатора гауссово распределение с минимальной шириной это­го распределения в поперечной плоскости, то простейшим п наи­более надежным способом селекции является диафрагмирование пучка внутри резоиатора. Если размер отверстия диафрагмы мал, то число Френеля для резонатора N_F = а /IX определяется этой диафрагмой. С уменьшением числа Френеля различие в дифрак­ционных потерях для основной моды п мод высших порядков возрастает, что и позволяет осуществлять их селекцию.

Зная расчетную зависимость дифракционных потерь основной и следующей за ней по порядку поперечных индексов моды от числа Френеля, можно определить требуемый радиус диафрагмы. При этом, однако, вносятся потери и в основную моду. Простую оценку поперечного размера диафрагмы можно сделать исходя из того, что этот размер должен быть примерно равен поперечно­му размеру распределения поля моды, следующей за основной, а место расположения диафрагмы должно быть выбрано там, где размеры мод отличаются наиболее сильно. Обычно, все же, раз­мер отверстия диафрагмы и ее месторасположение выбираются экспериментально.

Существенным недостатком обсуждаемого способа выделения основной моды в устойчивом резонаторе является малость попе­речных размеров моды. Это облегчает селекцию, но уменьшает выходную мощность, так как прп этом не весь объем активной среды оказывается охваченным электромагнитным полем. Для увеличения выходной мощности необходимо увеличение объема моды. Кардинальным решением является переход к неустойчивым резонаторам. Именно применение неустойчивых резонаторов яв­ляется эффективным средством селекции поперечных мод.

Селекция продольных мод. Частотная селекция, пространственная селекция тонкими поглотителями.

Вернемся к вопросу о селекции мод. В нашем предыдущем изложении неоднократно подчеркивалось, что переход к откры­тым резонаторным системам при резком укорочении длины волны, по сути дела, обусловлен необходимостью резкого разре­жения спектра колебаний, сгущающегося с ростом частоты про­порционально v². Изложенный выше материал показывает, что в открытых резонаторах это разрежение достигается путем увели­чения радиационных потерь нежелательных мод прп сохранении низкого уровня потерь желаемых (полезных) тппов колебаний.

Вместе с тем в открытых резонаторах, особенно в устойчи­вых резонаторах, спектр собственных колебаний остается все же слишком богатым с точкп зрения требований многих лазерных применений. Методы дальнейшей очистки этого спектра или, иначе говоря, методы улучшения модового состава лазерного из­лучения получили наименование селекции мод. Все методы се­лекции мод основаны на уже упомянутой идее увеличения по­терь энергии в резонаторе для нежелаемых мод прп сохранении высокой добротности резонатора для требуемой моды. При селек­ции поперечных мод (см. лекцию девятую) используется их различие в поперечной структуре поля. Продольные моды имеют одинаковую поперечную структуру поля, но различаются числом полуволн, укладывающихся между зеркалами резонатора. Сле­довательно, продольные моды отличаются частотой п расположе­нием узлов стоячей волны вдоль осп резонатора.

Наиболее общпй метод селекцпп продольных мод пспользует их 'отличие друг от друга по частоте и поэтому требует введе­ния в резонатор лазера узкополосных дисперсионных элементов. В качестве таких элементов могут быть использованы эталоны Фабри — Перо, призмы п дифракционные решетки, зеркала с частотно зависимыми коэффициентами отраженпя п т. п.

Простейшим является пспользованпе для селекцпп продоль­ных мод частотной зависимости усиления активного вещества лазера. Межмодовое расстояние для продольных мод составляет

Если расстояние между модами превышает ширину линии уси­ления:

а центральные частоты какой-то одной моды и линип усиления близки друг к другу:

то в лазере возбуждается одномодовая (в смысле продольной мо­ды) и тем самым одночастотная генерация. Частота генерации в этом случае в соответствии с формулой (6.33) определяется настройкой частоты моды на частоту линии и соотношением их добротностей. Этот метод селекции продольных мод может быть успешным в случае газовых лазеров, линии усиления которых достаточно узки. Примером может быть С0₂-лазер низкого дав­ления с шириной линии усиления 60 МГц и длиной резонатора 1м

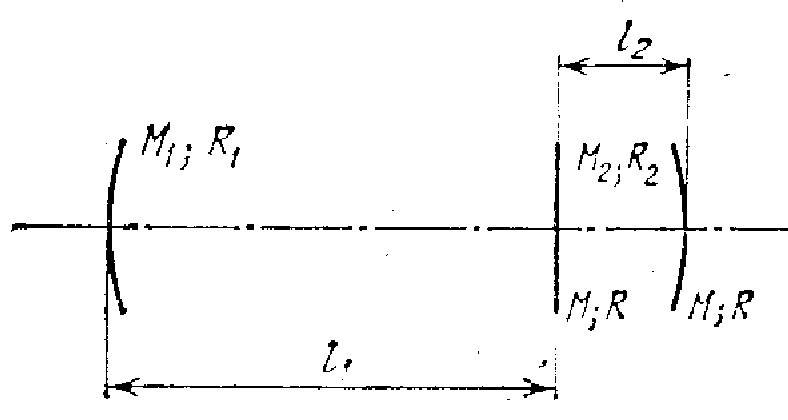
Рис. 10.3. Резонатор с диспер­сионным зеркалом R₂.

Однако в большинстве случаев линии уси­ления активных сред гораздо шире, и этот метод приводит; к неприемлемо коротким резонаторам.

Большое применение нашел метод дисперсионного зеркала. Рассмотрим схему, представленную на рис. 10.3. При l₂ < h в этом трехзеркальном резонаторе два правых зеркала можно рас­сматривать как единое зеркало с коэффициентом отражения R₂, зависящим от частоты. Оценить характер зависимости R₂(X) можно, используя формулу (6.7) для коэффициента пропускания регенерированного эталона Фабри — Перо. При К = 1 в приближе­нии плоских волн коэффициент пропускания двух параллельных зеркал с коэффициентами отражения R, разнесенными на рас­стояние 1₂, составляет в соответствии с (6.7)

Тогда коэффициент отражения эквивалентного зеркала R₂ равен

При

величина R₂ обращаемся в нуль, на этих частотах резонатор, образуемый зеркалами Ri и R₂, не имеет добротности, что и приводит к селекции соответствующих про­дольных мод. Схема, представленная на рис. 10.3, и формула (10.25) не могут претендовать на количественное описание про­цесса селекции продольных мод введением в резонатор лазера дополнительного дисперсионного элемента. Они приведены здесь лишь для иллюстрации идеи этого метода.

На практике используется множество модификаций метода селективного зеркала. При конструировании принимается во внимание необходимость согласования поперечного распределения поля, т. е. согласования мод, во всех резонансных объемах получаемого таким образом многозеркального резонатора и учитыва­ется взаимное влияние этих- парциальных резонаторов.

При селекции продольных мод в принципе может быть ис­пользовано различие в продольном распределении поля различ­ных мод. Каждая продольная мода представляет собой стоячую волну. Расстояние между узлами в этих стоячих волнах отлича­ется от моды к моде.

Рассмотрим моду с продольным индексом

Расстояние между ближайшими к зеркалу узлами мод g и q + 1 составляет:

и очень мало. При удалении от зеркала расстояние между узла­ми нарастает и для узла g-й моды номер q/2 составляет

что означает, что с узлом q-й моды совпала пучность g + 1-й люды. Это происходит на расстоянии

от зеркала, т. е. в середине резонатора. Но в этой точке находит­ся пучность q + 2-й моды, узел q + 3-й, пучность q + 4-й и т. д. Поэтому как-то использовать такое пространственное разнесение узлов и пучностей продольных мод для их эффективной селек­ции невозможно.

Очевидно, что общее число мод, среди которых надо произ­вести селекцию, составляет

Будем считать, что мы ищем способ выделить q-ю моду и что* ее центральная частота v_q совпадает с центральной частотой ли­нии усиления vn. Тогда номер наиболее далеких продольных мод, от которых желательно избавиться, равен q ± т/2. В районе пер­вого узла моды q расстояние между узлами все еще очень мало:

Номер N-го узла моды q, который первым совпадает с пучно­стью моды q ± т/2, определяется уравнением:

и составляет

Это произойдет на расстоянии

от зеркала. В этой точке расстояние между узлами ближайших мод q и q + 1 в соответствии с (10.27), (10.33), (10.30) и (10.26) равно

что для многих газовых лазеров составляет заметную долю дли­ны волны.

Изложенное подводит к мысли о возможности следующего метода селекции продольных мод.

Поместим в узел номер N желаемой моды q тонкий частично прозрачный поглотитель. Если его толщина много меньше дли­ны волны, то наличие поглотителя в узле, где напряженность

электрического поля моды q равна нулю, не вызывает потерь энергии из моды q. Все же остальные моды в этой точке на осп резонатора имеют ненулевую напряженность электрического по­ля и поэтому будут испытывать потери энергии, что и приведет к их дискриминации (рис. 10.4). Этот метод пространственной се­лекции продольных мод тонкими поглотителями нашел примене­ние для газовых лазеров, главным образом видимого диапазона. Тонкие частично прозрачные поглотители изготовляются нанесе­нием слоев металла толщиной 1—10 нм на оптически полиро­ванные прозрачные подложки.