А ‑ расчетная схема; б ‑ эпюра продольных сил; в ‑ эпюра напряжений; г ‑ эпюра продольных перемещений

Решение.

1. Построение эпюры N.

На брус действуют три си­лы, следовательно, про­­до­льная си­ла по его длине будет изменяться. Разбиваем брус на участки, в пределах которых про­­до­льная сила будет постоянной. В данном случае границами участков являются сечения, в ко­­торых приложены силы. Обозначим сечения буквами А, В, С, D, начиная со свободного конца, в данном случае правого.

Для определения продольной силы на каждом участке рассматриваем про­извольное поперечное сечение, сила в котором определяется по пра­вилу, приведенному ранее. Чтобы не определять предварительно реакцию в заделке D, начинаем расчеты со свободного конца бруса А.

Участок АВ, сечение 1-1. Справа от сечения действует растягивающая сила P₁ (рис. 15, а). В соответствии с упомянутым ранее правилом, по­лу­ча­ем

N_AB=+P₁=40 кН.

Участок ВС, сечение 2-2. Справа от него расположены две силы, на­правленные в разные стороны. С учетом правила знаков, получим

N_BС=+P₁-P₂=40-90=-50 кН.

Участок СD, сечение 3-3: аналогично получаем

N_СD=+P₁-P₂-P₃=40-90-110=-160 кН.

По найденным значениям N в выбранном масштабе строим эпюру, учи­тывая, что в пределах каждого участка продольная сила постоянна (рис.15,б)

Положительные значения N откладываем вверх от оси эпюры, отри­ца­тель­ные - вниз.

2. Построение эпюры напряжений σ.

Вычисляем напряжения в поперечном сечении для каждого участка бруса:

При вычислении нормальных напряжений значения продольных сил N берутся по эпюре с учетом их знаков. Знак плюс соответствует растя­же­нию, минус - сжатию. Эпюра напряжений показана на рис. 15, в.

3. Построение эпюры продольных перемещений.

Для построения эпюры перемещений вычисляем абсолютные удли­нения отдельных участков бруса, используя закон Гука:

Определяем перемещения сечений, начиная с неподвижного за­кре­плен­ного конца. Сечение D расположено в заделке, оно не может сме­щать­ся и его пере­мещение равно нулю:

∆_D=0.

Сечение С переместится в результате изменения длины участка CD. Пе­ремещение сечения С определяется по формуле

∆_C=∆l_CD=-6,7∙10^-4 м.

При отрицательной (сжимающей) силе точка С сместится влево.

Пере­мещение сечения В является результатом изменения длин DC и CB. Скл­а­дывая их удлинения, получаем

∆_B=∆l_CD+∆l_BC =-6,7∙10^-4 -2,1∙10^-4 = -8,8∙10^-4 м.

Рассуждая аналогично, вычисляем перемещение сечения А:

∆_A=∆l_CD+∆l_BC+∆l_AB =-6,7∙10^-4 -2,1∙10^-4 +0,57∙10^-4= -8,23∙10^-4 м.

В выбранном масштабе откладываем от исходной оси значения вычис­лен­ных перемещений. Соединив полученные точки прямыми линиями, стр­о­­­им эпю­ру перемещений (рис.15, г).

4. Проверка прочности бруса.

Условие прочности записывается в следующем виде:

σ_max≤[σ].

Максимальное напряжение σ_max находим по эпюре напряжений, выби­рая максимальное по абсолютной величине:

σ_max=267 Мпа.

Это напряжение действует на участке DC, все сечения которого являются опасным.

Допускаемое напряжение вычисляем по формуле:

Сравнивая σ_max и [σ], видим, что условие прочности не выполняется, так как максимальное напряжение превышает допускаемое.

Пример 4

Подобрать из условий прочности и жесткости размеры прямоугольного поперечного сечения чугунного стержня (см. рис. 16, а).

Дано: F=40 кН; l=0,4 м; [σ_p]=350 Мпа; [σ_с]=800 Мпа; Е=1,2∙10⁵ МПа; [∆l]=l/200; h/b=2, где h – высота, b – ширина поперечного сечения.

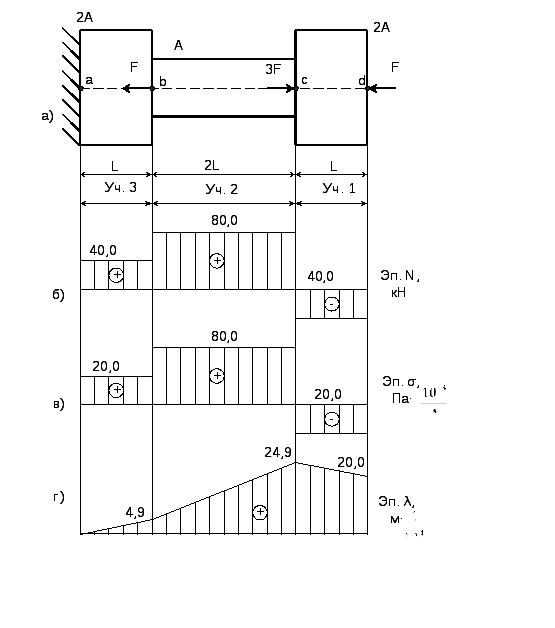
Рис.16

Решение.

1. Построение эпюры внутренних усилий N

Стержень разделен на 3 участка в зависимости от изменения внешней нагрузки и площади поперечного сечения. Применяя метод сечений, определяем продольную силу на каждом участке.

На участке 1: N₁=-F=-40 кН.

На участке 2: N₂=-F+3F=2F=80 кН.

На участке 3: N₃=-F+3F-2F=F=40 кН.

Эпюра N приведена на рис. 16, б.

2. Построение эпюры нормальных напряжений

Найдем напряжения на участках стержня.

На участке 1:

На участке 2:

На участке 3:

Эпюра σ приведена на рис. 16, в.

3. Нахождение площади поперечного сечения из условия прочности

Наибольшие растягивающие напряжения возникают на участке 2, наибольшие сжимающие напряжения – на участке 1. Для вычисления площади поперечного сечения используем условия прочности σ_max.p≤[σ_p] и σ_max.с≤[σ_с].

Напряжения на участке 1 равны

Тогда

Следовательно,

Напряжения на участке 2 равны

По условию прочности

Отсюда:

Напряжения на участке 3 равны

Тогда

Следовательно,

Необходимую площадь сечения следует принять из условия прочности при растяжении:

При заданном соотношении h/b=2 площадь поперечного сечения можно записать, как A=h∙b=2b². Размеры поперечного сечения будут равны:

4. Нахождение площади поперечного сечения из условия жесткости

При расчете на жесткость следует учитывать, что перемещение в точке d будет равно сумме деформаций всех участков стержня. Величину абсолютной деформации для каждого участка найдем по формуле

или

На участке 1:

На участке 2:

На участке 3:

Абсолютная деформация всего стержня:

Из условия жесткости ∆l≤[∆l], найдем

, откуда

Размеры поперечного сечения будут равны:

Сопоставляя результаты расчета на прочность и жесткость, принимаем большее значение площади поперечного сечения A=2,65 см².

5. Построение эпюры перемещений 𝜆

Для определения перемещения любого сечения стержня строят эпюру перемещений𝜆. За начало отсчета принимаем сечение в заделке, так как перемещение этого сечения равно нулю. При построении эпюры последовательно определяем перемещения характерных сечений стержня, которые равны алгебраической сумме изменений длин всех участков от начала отсчета до рассматриваемого сечения.

Сечение а:

Сечение b:

Сечение с:

Сечение d:

Эпюра перемещений λ представлена на рис.16, г.

Пример 5

Для ступенчатого бруса (рис. 17, а) при Е=2∙10⁵ Мпа, σ_Т= 240 МПа, требуется определить:

1. Внутренние продольные силы по его длине и построить эпюру продольных сил.

2. Нормальные напряжения в поперечных сечениях и построить эпюру нормальных напряжений.

3. Запас прочности для опасного сечения.

4. Перемещения сечений и построить эпюру перемещений.

Дано: F₁ = 30кН; F₂ = 20кН; F₃ = 60 кН; l₁ = 0,5м; l₂ = 1,5м; l₃ = 1м; l₄ = 1м; l₅ = l₆ = 1м; d₁ = 4см; d₂ = 2см.

Рис.17

Решение.

1. Определение продольных сил в характерных сечениях бруса, и построение эпюры продольных сил.

Изображаем расчетную схему (рис. 17,а) и определяем реакцию опоры в заделке, которую направляем с внешней стороны заделки влево. Если в результате определения реакции R_В окажется отрицательной, то это указывает на то, что ее направление противоположно. Ступенчатый брус под действием сил F₁, F₂, F₃ и реакции R_В находятся в равновесии, поэтому для определения R_В достаточно составить одно уравнение проекций всех сил на ось х, совпадающую с осью бруса.

ΣF_ix=-F₁-F₂+F₃-R_B=0

Откуда R_B=-F₁-F₂+F₃=-30-20+60=10 кН

Разграничим брус на участки. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и места изменения размеров поперечного сечения (рис. 17,а)

Пользуясь методом сечений, определяем для каждого участка величину и знак продольной силы. Проведем сечение 1–1 и рассмотрим равновесие правой отсеченной части бруса (рис. 17,б). Внутренние силы в каждом сечении условно направляем в сторону отброшенной части. Если внутренняя продольная сила положительна на участке, имеет место деформация растяжения; отрицательна – сжатие.

Рассматривая правую отсеченную часть, находим

ΣF_ix=-N₁-R_B=0; N₁=-R_B=-10 кН (сжатие)

Значение продольной силы в пределах первого участка не зависит от того, какую из отсеченных частей мы рассматривали. Целесообразнее всегда рассматривать ту часть бруса, к которой приложено меньше сил. Проведя сечения в пределах второго, третьего и четвертого участков, аналогично найдем:

для сечения 2–2 (рис. 17,в)

ΣF_ix=-N₂+F₃-R_B=0; N₂=F₃-R_B=60-10=50 кН (растяжение).

для сечения 3–3, рассматриваем левую часть бруса (рис. 17,г)

ΣF_ix=-F₁-N₃=0; N₃=F₁=30 кН (растяжение).

для сечения 4–4 (рис. 17,д)

ΣF_ix=N₄=0; N₄=0 эта часть бруса не испытывает деформации.

После определения внутренних продольных сил в характерных сечениях, строят график их распределения по длине бруса. График, показывающий, как изменяются продольные силы (N) при переходе от одного сечения к другому, т.е. график, изображающий закон изменения N вдоль оси бруса, называется эпюрой продольных сил.

Эпюра продольной силы строится в следующей последовательности. В разграниченном на участки брусе провести через точки приложения внешних сил линии, перпендикулярные его оси. На некотором расстоянии от оси бруса провести линию параллельную его оси: на перпендикуляре к этой линии отложить в выбранном масштабе отрезок, соответствующий продольной силе для каждого участка: положительные вверх от оси эпюры, отрицательные – вниз. Через концы отрезков провести линии, параллельные оси. Ось эпюры проводят тонкой линией, а саму эпюру очерчивают толстыми линиями, эпюру штрихуют тонкими линиями, перпендикулярными ее оси. В масштабе каждая линия равна продольной силе в соответствующем сечении бруса. На эпюре указывают знаки плюс и минус и в характерных ее точках, где изменяется сила, проставляют ее значение. В сечениях, в которых приложены сосредоточенные силы, на эпюре имеются скачки – резкое изменение продольной силы "Скачок" продольной силы равен внешней силе, приложенной в данном сечении, что является проверкой правильности построенной эпюры. На (рис. 18,б) построена эпюра продольных сил для заданного ступенчатого бруса.

2. Определение нормальных напряжений в поперечных сечениях бруса и построение эпюры нормальных напряжений.

Нормальные напряжения на каждом участке определяем по формуле σ=N/A, подставляя в ее значение сил (в Н) и площадей (в мм²). Площади поперечных сечений бруса определяем по формуле A=πd²/4

Тогда

Нормальные напряжения на участках I–VI равны соответственно:

I. т.к. N₄ = 0

II.

III.

VI.

V.

VI.

В пределах каждого участка напряжение одинаково, так как одинаковы во всех сечениях значения продольной силы и площади поперечного сечения. Эпюра σ очерчена прямыми, параллельными ее оси. Построение по вычисленным значениям эпюры представлена на (рис. 18,в).

3. Определение запаса прочности для опасного сечения.

Из эпюры нормальных напряжений, построенной по длине бруса видно, что наибольшее напряжение возникает в пределах четвертого участка σ_max=159,2 Н/мм², следовательно, запас прочности

4. Определение перемещений сечений и построение эпюры перемещений.

Для построения эпюры перемещений достаточно определить перемещения крайних сечений каждого участка. Перемещение сечения определим как алгебраическую сумму деформаций участков стержня, расположенных между этим сечением и заделкой, т.е. неподвижным сечением.

Абсолютные перемещения сечений вычислим по формулам:

Эпюра продольных перемещений представлена на (рис. 18,г). В случае проверки жесткости следует сравнить полученное максимальное значение ∆l = 1,55 мм с допускаемым [∆l] для данного бруса.

Рис.18

Пример 6

Для ступенчатого бруса (рис.19) требуется:

1. Построить эпюру продольных сил

2. Определить нормальные напряжения в поперечных сечениях и построить эпюру

3. Построить эпюру перемещений поперечных сечений.

Дано:

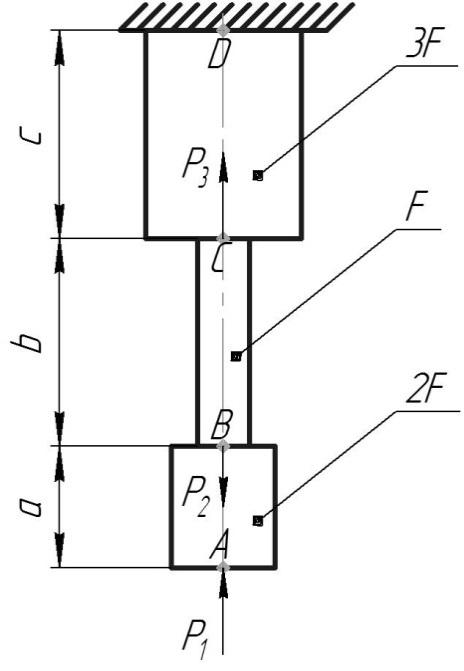
Рис.19

Решение.

1. Определим нормальные усилия

Участок AB:

Участок BC:

Участок CD:

Эпюра продольных сил показана на рис.20.

2. Определим нормальные напряжения

Участок AB:

Участок BC:

Участок CD:

Эпюра нормальных напряжений σ показана на рис.20.

3. Определим перемещения поперечных сечений

Эпюра перемещений δ показана на рис.20.

Эпюра	Эпюра	Эпюра

Рис.20

Пример 7

Для ступенчатого стального стержня (рис.21) требуется:

1. Построить эпюры продольных сил N и нормальных напряжений σ.

2. Определить продольную деформацию стержня ∆l.

Дано:

Е = 2∙10⁵ МПа; А₁ = 120 мм²; А₂ = 80 мм²; А₃ = 80 мм²; а₁ = 0,1 м; а₂ = 0,2 м; а₃ = 0,2 м; F₁ = 12 кН; F₂ = 18 кН; F₃ = -12 кН.

Решение.

1. Построение эпюр N и σ

Применяем метод сечений.

Участок 1.

ΣХ = 0 → -N₁ + F₁ = 0; N₁ = F₁ = 12 кН;

Участок 2.

ΣХ = 0 → -N₂ + F₂ + F₁ = 0;

N₂ = F₂ + F₁ = 18 + 12 = 30 кН;

Участок 3

ΣХ = 0 → - N₃ - F₃ + F₂ + F₁ = 0;

N₃ = - F₃ + F₂ + F₁= -12 + 18 + 12 = 18 кН;

2. Расчетная схема с истинным направлением внешней нагрузки и расчетными эпюрами.

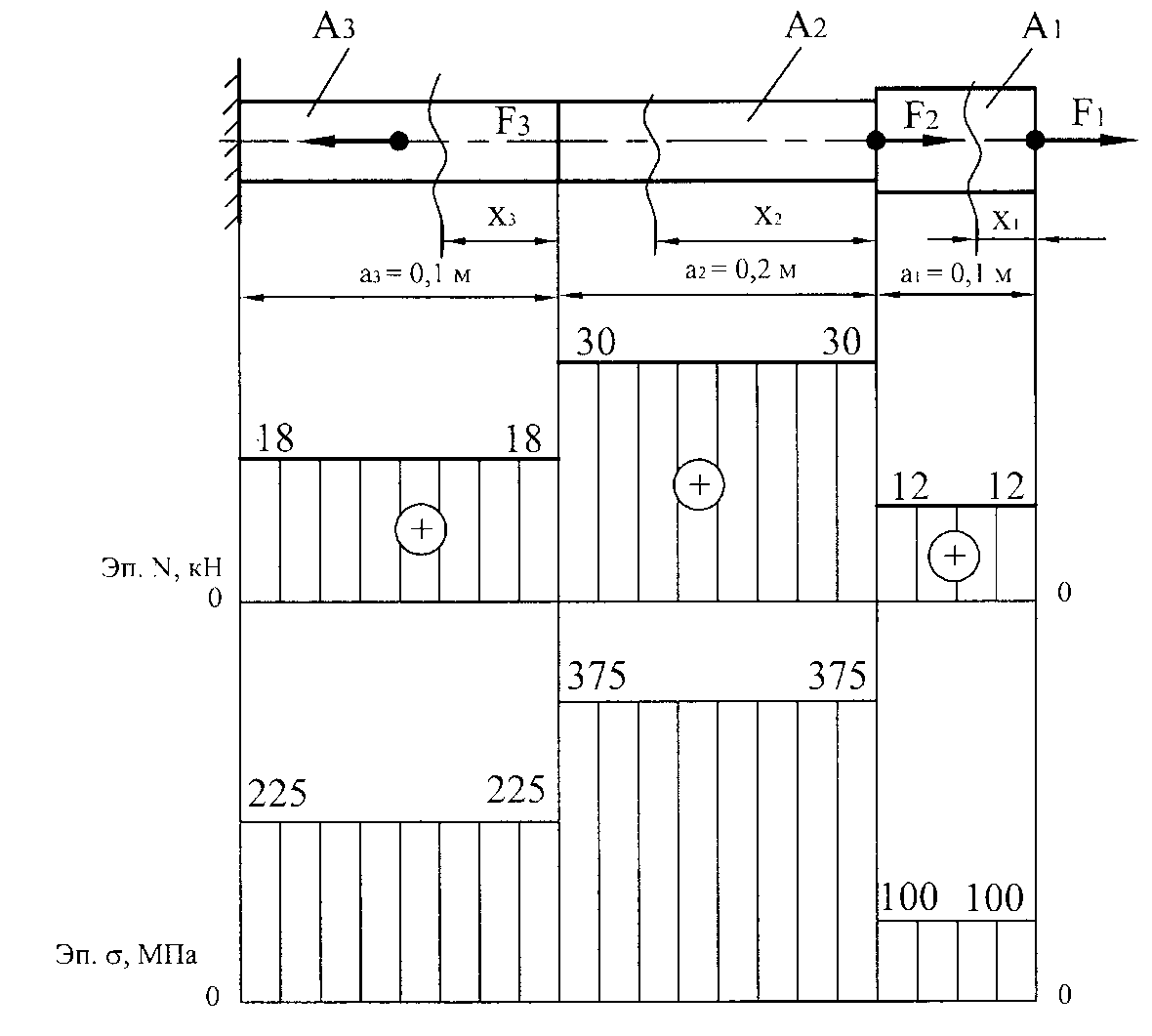
Рис.21

3. Определение продольной деформации стержня

Пример 8

Для бруса, жестко заделанного обоими концами и нагруженного вдоль оси силами F₁ и F₂ приложенными в его промежуточных сечениях (рис. 22,а), требуется

1) Построить эпюры продольных сил,

2) Построить эпюры нормальных напряжений

3) Построить эпюры перемещений поперечных сечений

4) Проверить прочность бруса.

Дано: если материал – сталь ст.3, F = 80 кН, σ_т = 240 МПа, А = 4 см², а = 1 м, требуемый коэффициент запаса [n] = 1,4, Е = 2∙10⁵ МПа.

Рис.22

Решение.

1. Статическая сторона задачи.

Поскольку силы F₁ и F₂ действуют вдоль оси стержня на его концах, под действием сил F₁ и F₂ в заделках могут возникнуть только горизонтальные опорные реакции R_А и R_В. В данном случае имеем систему сил, направленных по одной прямой (рис. 22,а), для которой статика дает лишь одно уравнение равновесия.

ΣF_ix = -R_А + F₁ + F₂ – R_В = 0; R_А + R_В = F₁ + F₂ = 3F (1)

Неизвестных реактивных сил две R_А и R_В, следовательно, система один раз статически неопределима, т.е. необходимо составить одно дополнительное уравнение перемещений.

2. Геометрическая сторона задачи.

Для раскрытия статической неопределимости, т.е. составления уравнения перемещений, отбросим одну из заделок, например правую (рис. 22,б). Получаем статически определимый брус, заделанный одним концом. Такой брус называют основной системой. Действие отброшенной опоры заменяем реакцией R_В = Х. В результате имеем статически определимый брус, нагруженный кроме заданных сил F₁ и F₂ неизвестной реактивной силой R_В = Х. Этот статически определимый брус нагружен так же как заданный статически неопределимый, т.е. эквивалентен ему. Эквивалентность этих двух брусьев позволяет утверждать, что второй брус деформируется так же, как первый, т.е. перемещение ∆_В – сечения В равно нулю, так как фактически (в заданном брусе) оно жестко заделано: ∆_В = 0.

На основе принципа независимости действия сил (результатом действия на тело системы сил не зависит от последовательности их приложения и равен сумме результатов действия каждой силы в отдельности) перемещение сечения В представим как алгебраическую сумму перемещений от сил F₁, F₂ и Х, т.е. уравнение совместности деформаций примет вид:

∆_B=∆_BF1+∆_BF2+∆_BX=0 (2)

В обозначениях перемещений первая буква индекса указывает о перемещении какого сечения идет речь; вторая – причину, вызывающую это перемещение (силы F₁, F₂ и Х).

3. Физическая сторона задачи.

На основании закона Гука выражаем перемещения сечения В, через действующие силы F₁, F₂ и неизвестную реакцию Х.

На (рис. 22, в, г, д), показаны схемы нагружения бруса каждой из сил в отдельности и перемещения сечения В от этих сил.

Пользуясь этими схемами, определяем перемещения:

равно удлинению участка АС;

равно удлинению участков АД и ДЕ;

равно сумме укорочений участков АД, ДК, КВ.

4. Синтез.

Подставим значения , , в уравнение (2), имеем

Откуда

Следовательно:

Подставляя R_В в уравнение (1), получим:

R_А + 66,7 =3∙80 = 240

отсюда R_А =240–66,7=173,3 кН, R_А = 173,3 кН, таким образом, статическая неопределимость раскрыта – имеем статически определимый брус, заделанный одним концом, нагруженный известными силами F₁, F₂ и Х = 66,7 кН.

Эпюру продольных сил строим как для статически определимого бруса. На основании метода сечений внутренние продольные силы в характерных участках равны:

N_АС = R_А = 173,3 кН;

N_СЕ = R_А - 2F = 173,3 - 80∙2 = 13,3 кН;

N_ЕВ = -R_А = - 66,7 кН.

Эпюра продольных сил представлена на (рис. 22, е). Значения нормальных напряжений в характерных сечениях определяем по формуле

Для участка АС

для участка СД

для участка ДЕ

для участка ЕК

для участка КВ

В пределах каждого из участников напряжения постоянны, т.е. эпюра "σ" – прямая, параллельная оси бруса (рис.22, ж).

При расчете на прочность интерес представляют те сечения, в которых возникают наибольшие напряжения. В рассмотренном примере они не совпадают с теми сечениями, в которых продольные силы максимальны, наибольшее напряжение возникает на участке ЕК, где σ_мах = - 166,8 МПа.

Из условия задачи следует, что предельное напряжение для бруса

σ_пред = σ_т = 240 МПа, поэтому допускаемое напряжение

Отсюда следует, что расчетное напряжение σ = 166,8 МПа < 171,4 МПа, т.е. условие прочности выполняется. Разница между расчетным напряжением и допускаемым составляет:

Перегрузка или недогрузка допускается в пределах ±5%.

При построении эпюры перемещений достаточно определить перемещения сечений совпадающих с границами участков, так как между указанными сечениями эпюра ∆l имеет линейный характер. Начинаем строить эпюру перемещений от левого защемленного конца бруса, в котором ∆_А = 0; так как оно неподвижно.

Итак, на правом конце бруса в сечении В, ордината эпюры ∆l равна нулю, так как в заданном брусе это сечение жестко защемлено, по вычисленным значениям построена эпюра ∆l (рис.22, з).

Пример 9

Для составного ступенчатого бруса, состоящего из меди и стали и нагруженного сосредоточенной силой F (рис. 23,а), определить внутренние продольные силы и построить их эпюры, если известны модули упругости материала: для стали E_c, для меди E_M.

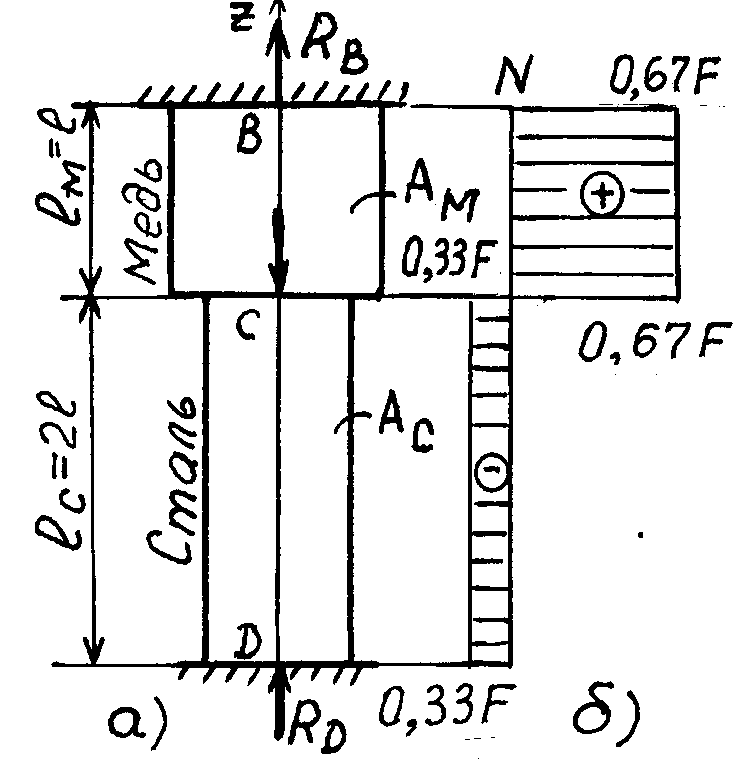
Рис.23

Решение.

1. Составляют уравнение статического равновесия:

ΣZ=0;R_B-F+R_D=0. (1)

Задача один раз статически неопределима, поскольку обе реакции могут быть определены только из одного уравнения.

2. Условие совместности перемещений должно выразить тот факт, что общая длина бруса не меняется, т.е. перемещения, например, сечения

(2)

Используя закон Гука σ=Eε, с учетом того факта, что перемещения какого-либо поперечного сечения бруса численно равны удлинению или укорочению его участков, расположенных между заделкойBи «перемещающимся» сечениемD, преобразуют уравнение (2) к виду:

Отсюда R_D=0,33F. (4)

Подставив (4) в (1), определяют

R_B=F-R_D=F-0,33F=0,67F. (5)

Тогда, применив метод сечений, согласно выражению N_i=ΣF_i, получают:

N_DC=-R_D;N_BC=R_B.

Приняв для наглядности решения

l_M=l; l_c=2l; A_M=4A_C; E_C=2E_M.

с учетом (4) получают N_DC=-R_D= -0,33F,

a с учетом (5) получают N_BC=R_B=0,67F.

Эпюра продольных сил N показана на рис. 16, б.

Расчет на прочность после этого выполняют согласно условию прочности

Пример 10

Брус ступенчато-переменного сечения, расчетная схема которого показана на рисунке 24, находится в условиях центрального (осевого) растяжения-сжатия под действием заданной нагрузки.

Требуется:

1) Раскрыть статическую неопределимость;

2) Построить эпюры нормальных сил и нормальных напряжений (в буквенном выражении величин);

3) Подобрать сечение бруса по условию прочности;

4) Построить эпюру продольных перемещений поперечных сечений.

Влиянием собственного веса бруса пренебречь, опорные устройства считать абсолютно жесткими.

Дано:

материал – чугун, допускаемые напряжения (расчетные сопротивления):

Принять:для чугуна

Параметр Fподлежит определению из условий прочности, а параметрP при выполнении п.3 задания, принять:

Примечание:

1) В расчетной схеме между нижним торцом бруса и опорой до нагружения бруса имеется зазор . Коэффициентпринять соответственно равным 1.

2) При отсутствии на расчетной схеме одной из сил P₁илиP₂соответствующий коэффициент (α₁или α₂) считать равным нулю

3) При выполнении п.3 задания следует пользоваться методом допускаемых напряжений

Рис.24

Решение:

1) В результате нагружения бруса, в его заделках возникают реакции направленные вдоль оси (рис.25). Определяем реакцию в заделке. Предварительно направляем ее вверх.

Рис.25

Составляем уравнение равновесия:

Это уравнение является единственным и содержит две неизвестные силы. Следовательно, система один раз статически неопределима.

Раскрываем статическую неопределимость:

Выразим удлинения через силы:

Подставим в уравнение равновесия:

Таким образом, статическая неопределимость раскрыта.

2) Разобьем брус на 3 участка (рис.26), начиная от его свободного конца; границами участков служат сечения, где приложены внешние силы, а также места изменения размеров поперечного сечения.

Рис.26

Произведем произвольное сечение 1 – 1 на участке I, и, отбросив верхнюю часть бруса, рассмотрим условия равновесия оставленной нижней части, изображенной отдельно (рис.27,б).

На оставленную часть действует сила R_B искомое усилие. Проектируя на осьZсилы, действующие остальную часть, получаем.

Отсюда .

Проведем произвольное сечение 2 – 2 на участке II, и, отбросив верхнюю часть бруса, рассмотрим условия равновесия оставленной нижней части, изображенной отдельно (рис.27,в).

.

.

Проведем произвольное сечение 3 – 3 на участке III, и, отбросив верхнюю часть бруса, рассмотрим условия равновесия оставленной нижней части, изображенной отдельно (рис.27,г).

.

.

Построим график (эпюру), показывающий, как меняется N по длине бруса (рис.27,д).

Эпюру нормальных напряжений получим, разделив значения Nна соответствующие площади поперечных сечений бруса, т.е.

Для Iучастка:

Для IIучастка:

Для IIIучастка:

Построим эпюру нормальных напряжений (рис.27, е).

3) Расчет прочности выполняется с использованием условий прочности. Условие прочности конструкции записывается в виде:

где – наибольшие расчетные растягивающие и сжимающие напряжения в конструкции;

–допускаемые напряжения при растяжении и сжатии соответственно.

Подбор сечения бруса в данном случае осуществляется по условию прочности третьего участка, т.к. на этом участке возникают наибольшие растягивающие напряжения:

откуда

Принимаем

По найденному значению параметра F определяем площади сечений участков бруса:

Подбор сечений чугунного бруса по условию прочности на сжатие производить не будем, т.к. наибольшее значения сжимающих напряжений меньше растягивающих, а

4) Построим эпюру продольных перемещений поперечных сечений. Она строится суммированием упругих удлинений участков, начиная с неподвижного конца.

Определим изменение длин участков бруса по формуле:

Для III участка–

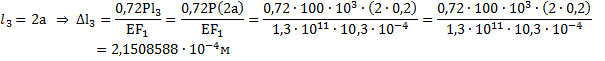
Для II участка–

Для I участка–

По условию в расчетной схеме между нижним торцом бруса и опорой до нагружения бруса (участок I) имеется зазор. Коэффициентпо условию равен 1, тогда зазор будет равен.

Находим осевые перемещения сечений бруса по границам участком:

Построим эпюру продольных перемещений поперечных сечений (рис.27, ж).

Рис.27

Пример 11

Для статически неопределимого стержня (рис.28) требуется построить эпюры продольных сил и нормальных напряжений.

Дано: l₁= 1 м;l₂= 0,8 м;F₂= 15 см²= 15·10^-4м²;F₂/F₁= 2,1;P=190 кН = 190·10³Н; ∆t= 30K; δ = 0,006 см = 6·10^-5м;E= 1·10⁵МПа =1·10¹¹Па; α= 17·10^-6K.