Пример 5.

Чугунная труба-стойка высотой с наружным диаметром и внутренним диаметром нагружена сжимающей силой , модуль упругости чугуна . Найти напряжение в поперечном сечении колонны, абсолютное и относительное укорочения .

Решение.

Как уже говорилось выше, решение задачи начинается с выбора расчетной схемы. В данном случае стойка изображается как вертикальный стержень длиной , жестко закрепленный в нижней части (условное изображение фундамента или земли). К верхней части стержня приложена сосредоточенная сжимающая сила (направление к стержню). При этом линия действия силы должна совпадать с осью стержня. Кроме того, рядом необходимо изобразить поперечное сечение стойки с указанием основных размеров. В данном примере – это кольцо. Расчетная схема для решения задачи изображена на рис. 2.13, а.

Далее строим эпюру продольной силы и определяем максимальное внутреннее усилие, возникающее в колонне. Поскольку внешняя нагрузка постоянна по высоте, то возникает только одна сжимающая продольная сила .

Рис. 2.13.

Максимальное нормальное напряжение определяется по формуле:

где – площадь трубы:

.

тогда:

Абсолютное и относительное укорочения стойки определяем по формулам:

Знак "минус" обозначает уменьшение размера (укорочение).

Пример 6.

Стальной стержень круглого сечения растягивается усилием . Относительное удлинение не должно превышать , а напряжение –. Найти наименьший диаметр, удовлетворяющий этим условиям, если модуль упругости стали .

Решение.

Как и ранее, решение задачи начинается с изображения расчетной схемы и построения эпюра продольных сил (рис. 2.14).

Рис.2.14

По условию задачи напряжение не должно превышать , в связи с чем данная величина может быть принята за расчетное сопротивление материала стойки на растяжение, то есть . По аналогии заданное относительное удлинение можно принять за предельно допустимое для данной стойки, то есть . В результате необходимо подобрать диаметр стойки, удовлетворяющий условию прочности и условию жесткости.

Продольное растягивающее усилие равно по величине внешней нагрузке, действующей на стержень

Требуемая площадь поперечного сечения колонны из условия прочности будет определяться выражением:

Зная требуемую площадь, выразим необходимый из условия прочности диаметр:

Условие жесткости при центральном растяжении-сжатии:

Выражаем из предельного неравенства требуемую из условия жесткости площадь поперечного сечения:

Диаметр стойки из условия жесткости определим по формуле:

Окончательно принимаем из двух диаметров больший,

Пример 7.

Определить грузоподъемность и удлинение балки, если .

Расчетная схема бруса и эпюра продольных сил изображены на рис. 2.15.

Рис.2.15

Решение.

Грузоподъемность бруса – это максимальная нагрузка, которую он может выдержать, не разрушаясь. Таким образом, необходимо определить требуемую нагрузку из условия прочности:

Согласно эпюре , тогда условие прочности примет вид:

Отсюда грузоподъемность бруса будет равна:

Для определения удлинения стержня разбиваем его на участки. Каждый участок, должен иметь постоянную жесткость и величину продольной силы. Таким образом, для данного бруса получаем три участка (на рис. 2.15 они обозначены римскими цифрами), тогда абсолютная деформация в общем виде будет определяться выражением:

,

в котором каждое слагаемое определяется отдельно:

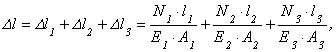
где - значения продольных сил соответственно на первом, втором и третьем участках; - длины соответственно первого, второго и третьего участков; - значения модулей упругости материалов бруса для каждого участка; - площади поперечных сечений стержня на первом, втором и третьем участках.

Поскольку жесткости всех трех участков одинаковые (балка изготовлена из одного материала и имеет постоянное по всей длине поперечное сечение), можно обозначить и вынести этот множитель за скобки. В результате получим выражение в виде:

где , , , , .

Пример 8.

Проверить прочность чугунного бруса (рис.2.16, а). Принять =150 МПа;=650 МПа, допускаемый коэффициент запаса прочности= 4.

Решение.

Строим эпюры продольных сил и нормальных напряжений(рис.2.16,б и в).

Рис.2.16

Напряжения на участках бруса

Так как материал бруса имеет различную прочность при растяжении и сжатии, проверку прочности следует выполнять для сжатого и растянутого участков, несмотря на то, что на участке напряжение значительно больше по абсолютному значению.

Коэффициенты запаса прочности

- прочность обеспечена;

- прочность обеспечена.

Из решения задачи можно сделать следующие выводы:

1) прочность стержня не обеспечена, так как на одном его участке коэффициент запаса прочности меньше требуемого;

2) на участках икоэффициент запаса прочности завышен, следовательно, эти участки бруса можно сделать меньшего диаметра. При проектировании элементов конструкций следует стремиться к тому, чтобы во всех сечениях коэффициент запаса прочности был равен или близок к требуемому.

Проверку прочности бруса можно было выполнить, используя условие прочности в виде , определив предварительно допускаемые напряжения по формулам

; .

Пример 1

На рис. 4,апредставлена схема бруса, нагруженного осевыми силами.

Требуется:

1) построить эпюру продольной силы;

2) построить эпюру перемещений.

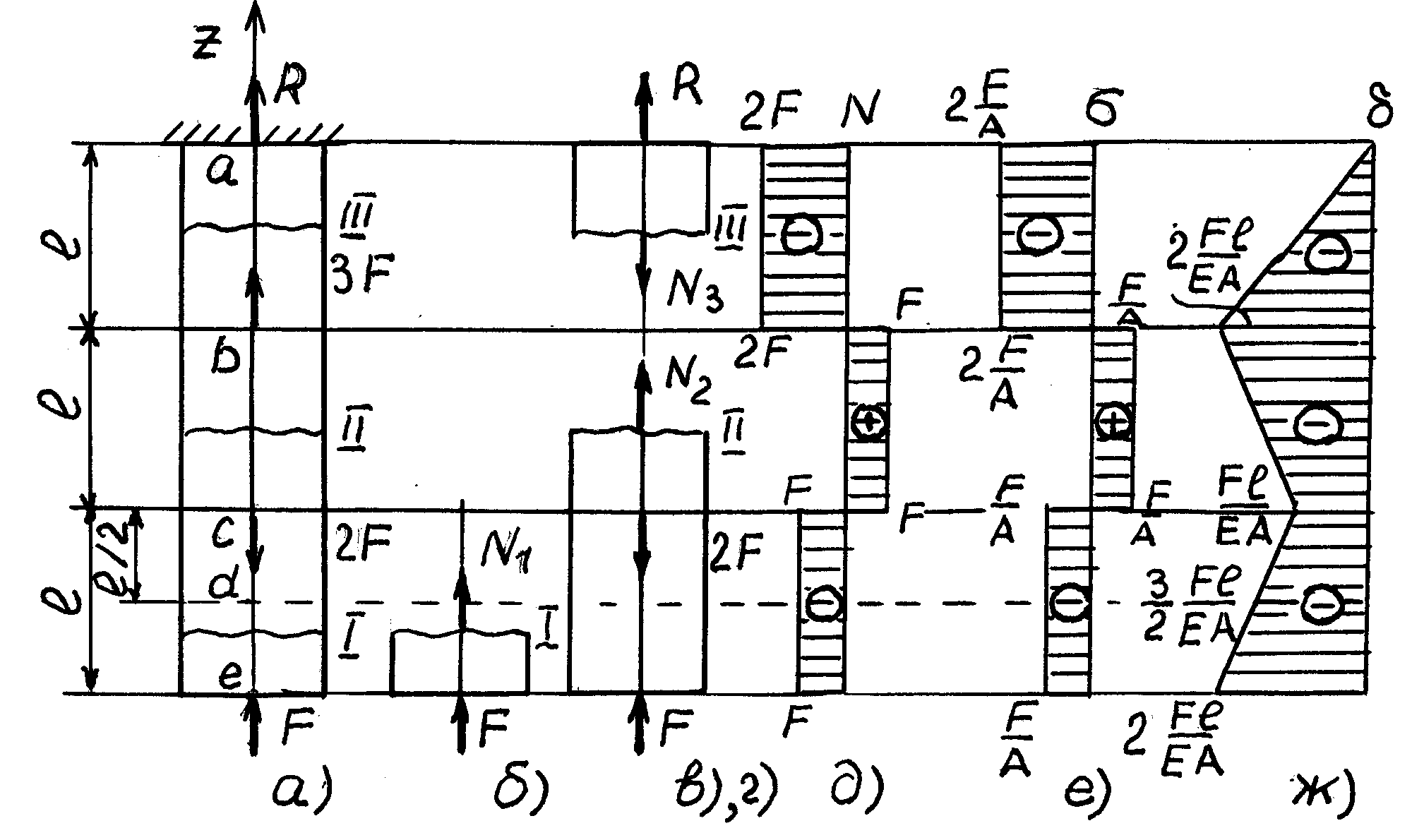
Рис.4

Решение.

Для контроля правильности расчета продольных сил определим реакцию Rв заделке, направив ее на растяжение по отношению к брусу. Используя уравнение равновесия и выбрав положительное направление продольной оси брусаZ, получим

ΣZ=0;R+3F-2F+F=0;R=-2F. (1)

Минус в ответе означает, что реакция направлена не на растяжение, как мы выбрали, а на сжатие.

Для определения продольных сил применим метод сечений.

1. Разбиваем брус на силовые участки I,II,III. Проводим на каждом участке произвольные поперечные сечения и отбрасываем части бруса.

2. Заменяем действие отброшенных частей бруса на каждом участке неизвестными продольными силами N₁,N₂,N₃,направив их от сечений, т.е. на растяжение (рис. 4, б, в, г).

3. Для каждого из участков составляем уравнение равновесия:

Участок I(рис. 4,б)ΣZ=0;N₁+F=0;N₁=-F;

Участок II (рис. 4, в) ΣZ=0;N₂-2F+F=0;N₂=F; (2)

Участок III(рис. 4,г)ΣZ=0; -N₃+R=0;N₃=-2F.

Отсюда имеем N_i=ΣF_i, (3)

т.е. продольная сила Nв произвольном сечении бруса численно равна алгебраической сумме проекций на продольную ось всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.

Это вывод позволит нам в дальнейшем определять продольные силы Nбез использования описанной процедуры составления уравнений равновесия. Так, например, согласно (3) для участкаIIполучаем

N₂=-F+2F=F.

4. По полученным данным строим график распределения продольных сил по длине бруса – эпюру продольных сил (рис. 4,д). Для построения эпюры проводим базовую линию (ось бруса) и, выбрав масштаб, откладываем на каждом участке величины продольных сил. Т.к. на схемах рис. 4,б, в, гпродольные силы были направлены на растяжение, то знаки в ответах поле решений уравнений равновесия (2) указывают: (+) – растяжение, (–) – сжатие. На эпюрах проставляют значения найденных продольных сил, их знак и наносят штриховку перпендикулярно оси бруса.

Из анализа эпюры Nвытекает следующееправило ее проверки:в поперечных сечениях бруса, в которых приложены внешние активные (F) или реактивные (R) силы, на эпюре продольных сил возникают скачки, равные по величине этим нагрузкам.

Определим полную абсолютную деформацию бруса, показанного на рис. 4, а. Зная продольные силыN₁,N₂,N₃, согласно (2) с учетом формулы получим:

Построенные эпюры перемещений δсечений бруса производят от заделки (или от любого конца, если брус не защемлен):

Выбирают масштаб и откладывают перемещения каждой точки (сечения) с учетом знаков. Полученную эпюру штрихуют (рис. 4, ж). Анализируя (4), видим, чтоперемещение любого поперечного сечения бруса численно равно удлинению (укорочению) части бруса, расположенного междузаделкой и этимсечением. Например, перемещение сеченияdравно:

Перемещение сечения d показано на эпюреδ(рис. 4,ж).