10.3. Методика оценивания результата измерений и его неопределенности

Оценивание результата измерений и его неопределенности проводится в следующей последовательности:

- составление уравнения измерений;

- внесение поправок и вычисление оценок входных величин;

- определение результата измерений;

- вычисление стандартных неопределенностей (типа А и В);

- вычисление суммарной стандартной неопределенности;

- выбор коэффициента охвата;

- составление бюджета неопределенности⁵ – таблица, в которой представлен полный перечень источников неопределенностей измерения с указанием их стандартной неопределенности и вклада в суммарную стандартную неопределенность результата измерений;

- оценка расширенной неопределенности результата измерений;

- представление результата измерений.

Составление уравнения измерения. В концепции неопределенности под уравнением измерения понимается математическая зависимость между измеряемыми величинами X₁, X₂,…X_k, а также другими величинами, влияющими на результат измерения X_k+1, X_k+2,…X_m, и результатом измерения Y

(10-1)

Величины X₁, X₂,…X_m называются входными величинами, используемые для оценивания неопределенности результата измерения, а результат измерения Y – выходной величиной измерения.

В качестве основы для составления уравнения измерения используется уравнение связи (в классическом понимании), т.е. зависимость Y = f(X₁, X₂,…X_k). Далее в результате анализа условий измерений и используемых СИ, устанавливаются другие факторы, влияющие на результат измерений. При этом величины X_k+1, X_k+2,…X_m, описывающие эти факторы включают в уравнение (10-1), даже если они незначительно могут повлиять на результат Y. Задача оператора – по возможности наиболее полно учесть все факторы, влияющие на результат измерения и описать их.

Внесение поправок и вычисление оценок входных величин. Внесение поправок – это устранение постоянных и переменных систематических отклонений (погрешностей), влияющих на результат измерений (гл.8). После внесения поправок измеряемых величин определяют оценки результатов измерений каждой входной величины X_i, где i = 1…m. Как известно, при нормальном распределении наилучшей оценкой этой величины является среднее арифметическое (формула 8-1)

, (10-2)

где q=1…n_i – количество измерений i – входной величины.

Результат измерения определяется как

(10-3)

Вычисление стандартных неопределенностей. Стандартную неопределенность типа А определяют как среднеквадратическое отклонение по формуле (8-3):

, (10-4)

т.е. используют те же формулы, что и для оценивания результата измерения и его рассеивания в классической теории оценки погрешности измерения (табл.8-1).

Для вычисления стандартной неопределенности по типу В рассматривают и используют различные факторы, которые могут оказать влияние на полную (общую) неопределенность измерений [5,6,60]:

- данные предыдущих измерений величин, входящих в уравнение измерения;

- сведения, имеющиеся в метрологических документах по поверке, калибровке и сведения изготовителя о приборе;

- сведения о предполагаемом вероятностном распределении значений величин, имеющихся в научно-технических отчетах и литературных источниках;

- данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих (подобных) СИ и материалов;

- неопределенность используемых констант и справочных данных;

- нормы точности измерений, указанные в технической документации на СИ;

- процесс осуществление выборки;

- транспортирование, хранение и обработка образцов;

- подготовка образцов;

- характер окружающих условий при проведении измерений;

- квалификация персонала, выполняющего измерения или испытания;

- отклонения от установленной процедуры при проведении измерений;

- неопределенность стандартных образцов или мер;

- программное обеспечение;

- неопределенности, связанные с внесением поправок;

- другие сведения об источниках неопределенностей, влияющих на результат измерения.

Пример 10-1. Государственный первичный эталон единицы температуры в диапазоне 0 – 962,78 ⁰С представляет собой комплекс аппаратуры для воспроизведения Международной температурной шкалы МТШ-90 с наивысшей в РФ точностью. При определении характеристик точности этого эталона выделяют следующие неопределенности типа В (сайт ВНИИФТРИ: Temperatures.ru):

- свойства электроизмерительного оборудования, в том числе нелинейность измерительного моста;

- градуировка образцовых мер сопротивления;

- наличие примесей в металле реперной точки;

- наклон площадки затвердевания вещества реперной точки;

- нагрев термометра измерительным током;

- гидростатический эффект (изменения температуры фазового перехода с глубиной погружения термометра);

- отвод тепла по термометру;

- отклонение давления в ампуле реперной точки от стандартного давления.

При расчетах принимается, что все указанные неопределенности распределены по равномерному закону.

Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных границах (нижней b_i- и верхней b_i+) для i-ой входной величины. При этом стандартную неопределенность по типу В определяют по известной формуле для среднеквадратического отклонения результатов измерений, имеющих равномерный закон распределения (разд. 8.2):

, (10-5)

а для симметричных границ , по формуле

(10-6)

Конечно в случае других законов распределений входных величин для вычисления неопределенности по типу В должны использоваться иные соотношения. Для определения коэффициента охвата можно воспользоваться данными табл. 10-2 [5, 6].

Таблица 10-2

Значения коэффициента охвата при различных предполагаемых

распределениях входной величины

Предполагаемое распреде-ление неопределенности входной величины	Вероятность охвата Р, которой соответствует U(xi)	Коэффициент охвата k
Равномерное распределение	0,99 – 1,0	1,71 - 1,73
	0,95	1,65
Нормальное распределение	1,0 (предел допускаемых значений)	3
	0,997	3
	0,99	2,6
	0,95	2
Неизвестное распределение		2

Примечание. Если известны граница суммы неисключенных систематических погрешностей θ(Р), распределенных по равномерному (равновероятному) закону, то стандартная неопределенность должна вычисляться по формуле (8-38)

(10-7)

где k – коэффициент охвата, зависящий от числа m суммируемых неисключенных неопределенностей типа В и зависящий от доверительной вероятности Р. Коэффициент охвата k=1,1 при Р=0,95; k=1,4 при Р=0,99 и m>4. Формула (10-7) получается из следующего преобразования:

(10-8)

Неопределенности входных величин могут быть коррелированны. Для вычисления коэффициента корреляции используют согласованные пары результатов измерений. Вычисления проводят по формуле (9-14)

Вычисление суммарной стандартной неопределенности. Суммарную неопределенность выходной величины определяют по тем же формулам, которые используются для расчета погрешностей косвенных измерений в концепции погрешности измерений.

В случае некоррелированных оценок входных величин, суммарную стандартную неопределенность вычисляют по формуле (разд. 9.3.1. и 9.3.2.):

(10-9)

где – коэффициенты чувствительности выходной величины по отношению к входной величинеx_i, u(x_i) – стандартные отклонения по типу А и/или В.

Оценка расширенной неопределенности результата измерений. Оценка расширенной неопределенности равна произведению стандартной неопределенности u_с(y) результата измерений на коэффициент охвата k:

U_р(y) =k u_с(y) (10-10)

Руководство рекомендует рассматривать все результаты измерений при доверительной вероятности (вероятности охвата) Р=0,95, определяя число степеней свободы по эмпирической формуле Велча-Саттерствейта

(10-11)

Используя таблицы распределения Стьюдента, коэффициент охвата при вероятности Р=0,95 определяется по формуле (прил.11).

Формулу для оценки суммарной стандартной неопределенности (10-9) можно записать в более простом виде

, (10-12)

также как и формулу (10-11) для определения числа степеней свободы

, (10-13)

где – число степеней свободы припрямых измерениях входной величины, n – число прямых измерений, – оценка стандартных неопределенностей типа А и В, соответственно.

При оценке вклада неопределенности по типу А принимают , а по типу В. При этих условиях, можно показать, что, если по типу А оценивается неопределенностьтолько одной входной величины, то формула (10-13) упрощается

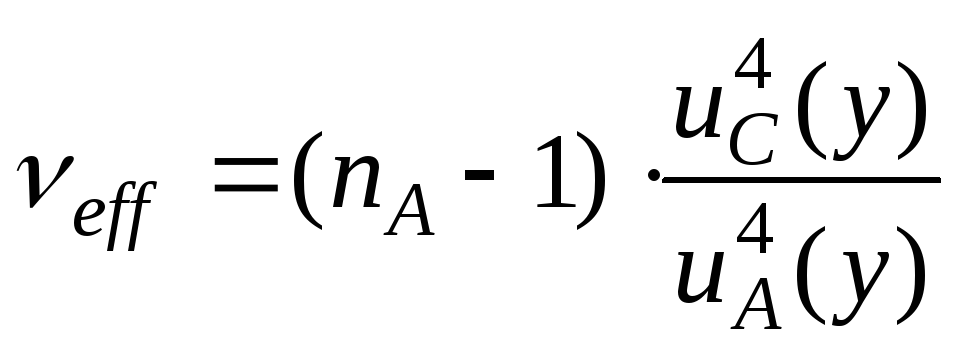, (10-14)

где n_A – число повторных измерений входной величины, оцениваемой по типу А.

Представление результата измерений. При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации, чтобы можно было проанализировать и/или повторить весь процесс получения результата измерений и вычисления неопределенностей, а именно:

- алгоритм получения результата измерений;

- алгоритм расчета всех поправок для исключения систематических погрешностей и их неопределенней;

- неопределенности всех используемых данных и способы их получения;

- алгоритмы вычисления суммарной и расширенной неопределенностей, включая значение коэффициента охвата k.

В документации по результатам измерений необходимо представлять:

u_c – суммарную неопределенность;

U_p(y)– расширенную неопределенность при вероятности Р;

k – коэффициент охвата;

u_i – данные о входных величинах;

–эффективное число степеней свободы.

Например, если результатом измерения является длина детали, то в протоколе измерений, как правило, делается следующая запись: «Длина детали составляет 153,2 мм. Расширенная неопределенность результата измерений составляет ± 1,4 мм при коэффициенте охвата равном 2» или «Измерения показали, что длина детали находится в интервале (151,8 – 154,6) мм при коэффициенте, равном 2». По умолчанию предполагается, что эти результаты соответствуют вероятности охвата 0,95.