Лекция 5

Тема: Магнитные элементы электронных устройств

В лекции рассматриваются вопросы:

1. Магнитные реакторы

2. Параметрические магнитные элементы

3. Магнитные параметрические стабилизаторы напряжения

4. Феррорезонансные ячейки

5. Магнитные формирователи и распределители импульсов

Литература

1 Магнитные реакторы

В источниках вторичного электропитания реактор – это элемент, предназначенный для накопления магнитной энергии с целью последующего использования ее в электрической цепи. В источниках вторичного электропитания используются два основных типа реакторов:

• реакторы фильтров;

• коммутирующие реакторы.

Реакторы фильтров работают при значительном подмагничивающем поле – В₀. Для них очень часто В₀>>В_~ (где В_~ - значение переменной составляющей магнитной индукции).

Коммутирующие реакторы предназначены для схем искусственной коммутации преобразователей. Они работают при малом (или равном нулю) подмагничивающем поле и значительном переменном поле (В₀<< В_~).

Основным параметром реактора является его индуктивность.

По определению индуктивность (или коэффициент самоиндукции):

(5.1)

где R_M – магнитное сопротивление магнитопровода (возможно и с зазором);

µ_а = µ₀ ·µ - абсолютная магнитная проницаемость материала;

l_ср – длина средней линии магнитопровода;

S_M - площадь его поперечного сечения.

Если обмотка реактора намотана на магнитопроводе без зазора (или с пренебрежимо малым зазором), то К = 1, и его индуктивность определяется следующим образом:

( 5.2)

Если реактор изготовлен на магнитопроводе с незначительным (по сравнению с длиной средней линии) зазором, то К и L определяются с приемлемой для практических расчетов точностью с помощью соотношений:

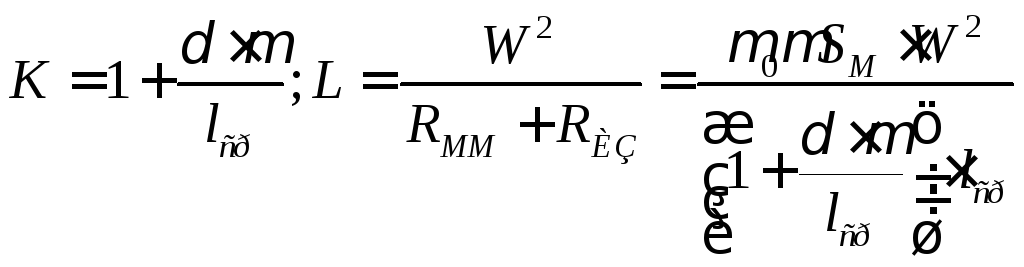(5.3)

Если в реакторе используется магнитопровод с большим зазором или вообще отсутствует магнитопровод, то хотя формула и справедлива, однако ее не используют, т.к. К найти в ряде случаев затруднительно. Индуктивность таких реакторов можно определить, используя справочную литературу.

Различают статическую индуктивность идинамическую индуктивность

Для реактора с магнитопроводом L_ст и L_Д определяются по формулам (5.2 и 5.3) при подстановке в качестве магнитной проницаемости µ_аст и µ_ад.

Для реактора без магнитопровода L_ст = L_Д.

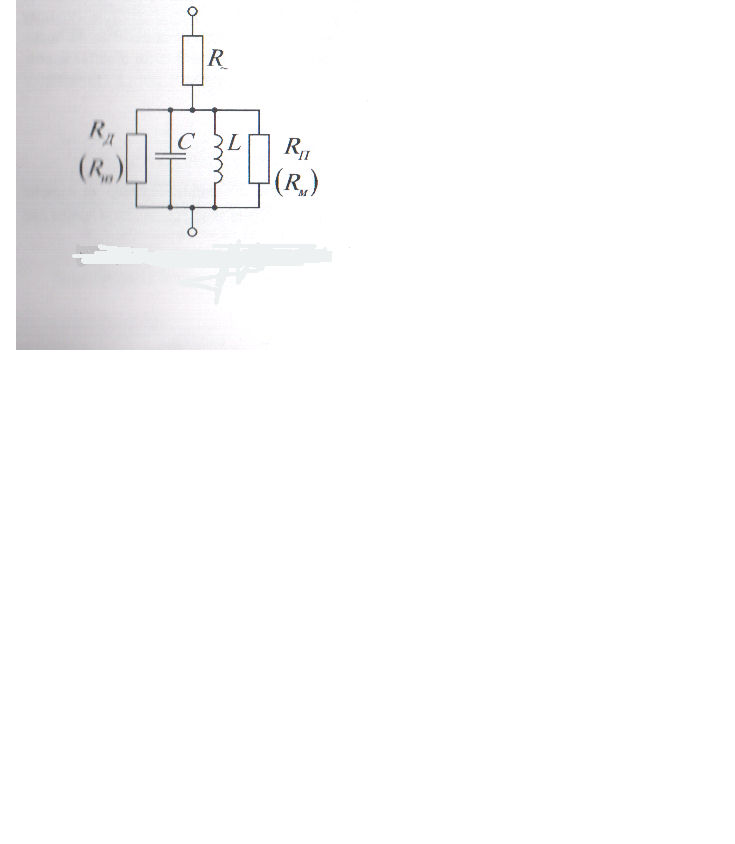
Рисунок 1

Кроме индуктивности реактор характеризуется и другими параметрами.

Эквивалентная схема реактора представлена на рисунке 1.

Емкость реактора (С) обусловлена емкостью обмотки относительно магнитопровода и относительно корпуса, а также емкостями между отдельными слоями обмотки и емкостями между витками.

Определение этих емкостей проводится аналогично определению паразитных емкостей трансформатора.

При высокой частоте периодического воздействия в магнитопроводе реактора возникают значительные потери мощности. В эквивалентной схеме они учитываются сопротивлением:

(5.4)

где U – действующее значение напряжения на реакторе.

При большой скорости изменения напряжений и токов в проводниках обмотки происходит вытеснение тока к поверхности проводника. Эффективное сечение проводника уменьшается, а его сопротивление должно увеличиваться. Сопротивление обмотки реактора с учетом добавочных потерь на эквивалентной схеме отражено резистором R_~.

Уменьшается также и индуктивность реактора. Это уменьшение зависит от конструкции обмотки и от выбранного провода.

Однако индуктивность обмотки, намотанной ленточным проводником, практически не меняется. Формулы, определяющие индуктивность витка из ленты прямоугольного сечения на низкой и высокой частоте, имеют вид:

(5.5)

(5.6)

где r – радиус витка, b – ширина ленты, a – толщина ленты, причем b>>a, g – среднее геометрическое расстояние периметра поперечного сечения ленты от самого себя. При b>>a величина g = 0,223b.

Таким образом, L_B ≈ L_Н. Физически это объясняется тем, что вытеснение тока происходит не в радиальном, а в осевом направлении сечения ленты.

В однослойных и одновитковых обмотках реакторов, намотанных круглым или прямоугольным проводом, уменьшение индуктивности с ростом частоты также незначительно. Это объясняется тем, что перераспределение тока по сечению провода мало изменяет картину магнитного поля во внешнем по отношению к проводнику пространстве, которое в основном и определяет индуктивность системы.

В многослойных обмотках магнитный поток, проходящий в области, непосредственно занятой обмоткой, составляет заметную величину по сравнению с общим потоком. Поэтому размагничивающее действие вихревых токов, возникающих в проводниках обмотки на повышенных частотах (эффект близости), существенно уменьшает магнитный поток обмотки и, следовательно, уменьшает ее индуктивность. Изменение индуктивности в зависимости от частоты можно оценить по формулам:

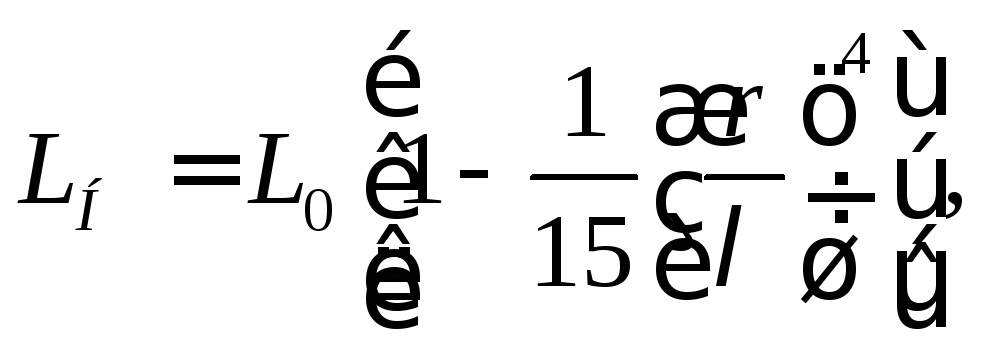(5.7)

(5.8)

В этих формулах: L₀ – индуктивность многослойной обмотки на частоте ƒ=0,

r – радиус провода,

m – число слоев обмотки,

γ – удельная проводимость материала,

λ – длина электромагнитной волны при синусоидальном токе:

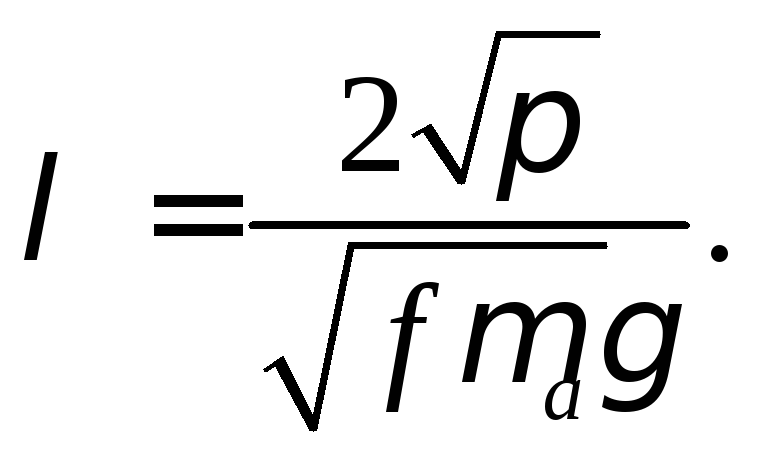(5.9)

Энергия, которую может накопить реактор в любой момент времени определяется как:

(5.10)

Ее максимальное значение:

(для синусоидальной формы тока), (5.11)

где I_m – амплитудное значение тока;

I_эфф = I – эффективное или действующее значение переменного тока за время его действия. В дальнейшем величину LI² будем называть энергоемкостью реактора.

Если по обмотке реактора протекает ток, имеющий переменную и постоянную составляющие, то энергоемкость реактора:

(5.12)

Под добротностью реактора понимают отношение реактивной энергии, запасенной в нем, к энергии потерь или отношение реактивной (в данном случае индуктивной) составляющей полного сопротивления реактора к активной его части.

Из анализа эквивалентной схемы реактора его добротность будет определяться из выражения:

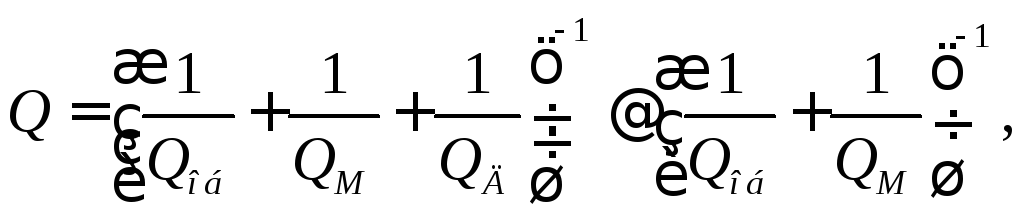(5.13)

где Q_об = ωL/R_~ - добротность обмотки;

Q_M = ωL /R_П – добротность магнитопровода;

Q_Д = ωL /R_Д – добротность диэлектрика (изоляции);

R_~, R_П, R_Д – соответственно сопротивление обмотки; сопротивление, учитывающее потери в магнитопроводе; сопротивление изоляции;

так как Q_Д >>Q_об, Q_M.

Признаком правильного проектирования является выполнение условия:

,

где С – собственная емкость реактора

Это означает, что рабочая частота должна быть значительно ниже частоты собственного резонанса. В противном случае не будет обеспечиваться заданная индуктивность.

Из рассмотрения последнего выражения (5.13) можно сделать следующие выводы:

• на величину добротности реактора существенным образом влияет качество материала магнитопровода и изоляции;

• для снижения потерь в изоляции (увеличение Q_Д) следует применять материалы с низкими значениями относительной диэлектрической проницаемости (ε_r) и тангенса угла диэлектрических потерь (tgδ);

• для увеличения Q_M следует применять материалы с малыми потерями (ферриты и магнитодиэлектрики) или вообще использовать воздушные реакторы.

Эти реакторы при большой энергоемкости имеют меньшие габариты, чем реакторы с ферромагнитным магнитопроводом. Кроме того, они имеют еще одно существенное преимущество – это независимость параметров реактора от величины протекающего по нему тока.

Чтобы улучшить добротность реакторов, изготовленных на магнитопроводах с низкой добротностью (использование различных марок электротехнических сталей) в магнитопровод вводят немагнитный промежуток.

Влияние немагнитного промежутка в магнитопроводе на параметры реактора. Немагнитный зазор в магнитопроводах реакторов и трансформаторов вводится для различных целей.

1. Приближение нелинейной характеристики магнитопровода к линейной.

В реакторе фильтра зазор уменьшает намагничивающее влияние постоянной составляющей тока.

Аналогичное действие оказывает зазор в магнитопроводах трансформаторов.

2. Если напряжение, воздействующее на первичную обмотку трансформатора, имеет прямоугольную или другую симметричную относительно оси абсцисс форму, то в силу неидентичности выходного каскада генераторного устройства, обусловленного разбросом параметров полупроводниковых приборов, положительные и отрицательные части напряжения оказываются несимметричными. В результате в первичной обмотке возникает несбалансированная постоянная составляющая намагничивающего тока, вызывающая в магнитопроводе постоянную составляющую магнитного потока. Подобное же явление наблюдается в трансформаторе со вторичной обмоткой со средней точкой при неполной симметрии полуобмоток. В обоих случаях постоянная составляющая магнитного потока гасится немагнитным зазором. Величина зазора должна выбираться такой, чтобы удовлетворялись следующие два условия:

а) магнитное сопротивление зазора должно в значительной степени превосходить сопротивление магнитопровода (составить 70…90% от общего сопротивления магнитной цепи);

б) индуктивность намагничивания при наличии зазора в магнитопроводе должна быть такой, чтобы обеспечивалась нормальная работа трансформатора. Математически эти условия выражаются следующим образом: R_м.з >R_м.м; L_1n = (5…10) R′_н, где R′_н – сопротивление нагрузки, приведенное по виткам к первичной стороне.

3. При необходимости изготовить реактор с малой индуктивностью, но со значительной величиной тока в обмотке. Тогда, чтобы разместить обмотку, намотанную проводом большого сечения, используют магнитопровод с зазором.

4. С помощью немагнитного зазора можно не только уменьшить, но и увеличить магнитную проницаемость, если к обмотке приложено напряжение

При неизменной переменной составляющей магнитного потока постоянную составляющую можно менять с помощью немагнитного зазора.

5. Подбором величины немагнитного зазора можно уменьшить объем магнитопровода реактора. Подбор такого зазора, при котором реактор обладает наибольшей индуктивностью, наибольшей добротностью и наименьшим объемом при заданной энергоемкости, называют оптимизацией немагнитного зазора.