
- •1. ПРЕДЫСТОРИЯ
- •2. НАЧАЛО ИСТОРИИ ЯДЕРНОЙ ФИЗИКИ
- •3. ЭПОХА ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ ИДЕЙ ЯДЕРНОЙ ФИЗИКИ
- •4. СОВРЕМЕННАЯ ЯДЕРНАЯ ФИЗИКА
- •5. РАЗВИТИЕ МЕТОДОВ РЕГИСТРАЦИИ ИЗЛУЧЕНИЙ
- •6. РАЗВИТИЕ УСКОРИТЕЛЬНОЙ ТЕХНИКИ
- •7. РАЗВИТИЕ РЕАКТОРОСТРОЕНИЯ
- •1. ОСНОВНОЙ ЗАКОН РАДИОАКТИВНОГО РАСПАДА
- •2. СТАТИСТИКА РАСПАДА
- •3. РАСПАД СМЕСИ РАДИОНУКЛИДОВ
- •4. ПРОЦЕССЫ НАКОПЛЕНИЯ И РАСПАДА ГЕНЕТИЧЕСКИ СВЯЗАННЫХ РАДИОНУКЛИДОВ
- •4.1 Цепочка из двух изотопов
- •4.2 Цепочки из трёх и более изотопов
- •4.3 Радиоактивные равновесия
- •4.3.1 Случай отсутствия равновесия
- •4.3.2 Подвижное равновесие
- •4.3.3 Вековое равновесие
- •4.4 Разветвленный распад
- •4.5 Степень равновесности
- •4.6 Примеры радиоактивных распадов
- •1. ПРИМЕРЫ РАДИОАКТИВНЫХ СЕМЕЙСТВ
- •1.1 Семейства урана, тория и актиния
- •1.2 Семейство нептуния
- •2. ПРИРОДНЫЕ РАДИАКТИВНЫЕ СЕМЕЙСТВА
- •3. ТЕХНОГЕННЫЕ РАДИОНУКЛИДЫ – РОДОНАЧАЛЬНИКИ ЕСТЕСТВЕННЫХ РЯДОВ
- •4. ОТКРЫТОСТЬ СИСТЕМЫ И СДВИГИ РАДИОАКТИВНЫХ РАВНОВЕСИЙ
- •5. КОНЦЕПЦИЯ ЭКВИВАЛЕНТНОСТИ РАДИОТОКСИЧНОСТИ ПРИРОДНЫХ И РЕАКТОРНЫХ РАДИОАКТИВНЫХ СЕМЕЙСТВ
- •6. РАДИОАКТИВНЫЕ ЦЕПОЧКИ ТЕХНОГЕННЫХ НУКЛИДОВ
- •1. ЯВЛЕНИЕ ИЗОТОПИИ
- •1.1 Историческая справка
- •1.2 Изотопы и изобары
- •1.3 Применение изотопов
- •2. ЯДЕРНО-ФИЗИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ИЗОТОПОВ
- •3. КОММЕРЧЕСКИЕ РАДИОАКТИВНЫЕ ИЗОТОПЫ
- •4. ИЗОТОПНЫЕ ЭФФЕКТЫ
- •5. АНАЛИЗ ИЗОТОПНОГО СОСТАВА
- •6. РАЗДЕЛЕНИЕ ИЗОТОПОВ
- •6.1 Общие замечания
- •6.2 Газовая диффузия
- •6.3 Диффузия в потоке пара (противопоточная масс-диффузия)
- •6.4 Термодиффузия
- •6.5 Газовое центрифугирование
- •6.6 Электромагнитное разделение.
- •6.7 Химическое обогащение
- •6.8 Аэродинамическая сепарация
- •6.9 AVLIS (испарение с использованием лазера).
- •6.10 Дистилляция
- •6.11 Электролиз
- •6.12 Изотопный обмен
- •7. ПРОИЗВОДСТВО ИЗОТОПОВ
- •7.1 Производство стабильных изотопов
- •7.2 Получение изотопов в ядерных реакторах
- •7.3 Получение изотопов на ускорителях
- •1. ИОНИЗИРУЮЩЕЕ ИЗЛУЧЕНИЕ И ЕГО ПОЛЕ
- •2. ВИДЫ ИЗЛУЧЕНИЙ
- •2.1. Корпускулярное излучение
- •2.1.1 Альфа-излучение
- •2.1.2 Протонное излучение
- •2.1.3 Нейтронное излучение
- •2.1.4 Электронное излучение
- •2.1.5 Бета-излучение
- •2.2 Космическое излучение.
- •2.3 Электромагнитное излучение
- •2.3.1 Рентгеновское излучение
- •2.3.2 Гамма излучение
- •2.3.3 Тормозное излучение
- •2.3.4 Излучение Черенкова-Вавилова
- •2.3.5 Синхотронное излучение
- •2.3.6 Переходное излучение
- •3. СВОЙСТВА ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ
- •4. ИСТОЧНИКИ ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ
- •4.1 Терминология: радиоактивные источники излучений и их характеристики
- •4.2 Классификация источников излучения.
- •4.2.1 Источники рентгеновского излучения.
- •4.2.2 Ускорители
- •4.2.3 Нейтронные источники
- •1. ПРОХОЖДЕНИЕ ИЗЛУЧЕНИЯ СКВОЗЬ ВЕЩЕСТВО
- •1.1 Терминология: взаимодействие ионизирующих излучений со средой
- •1.2 Типы взаимодействия излучения с веществом
- •1.3 Ионизация и возбуждение
- •2. ВЗАИМОДЕЙСТВИЕ ТЯЖЕЛЫХ ЧАСТИЦ С ВЕЩЕСТВОМ
- •2.1 Взаимодействие заряженной частицы с электроном
- •2.2 Ионизация и возбуждение атома
- •2.3 Тормозная способность
- •2.4 Пробег
- •3. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ С ВЕЩЕСТВОМ
- •3.1 Потери энергии движущимися электронами
- •3.2 Эффективный пробег электронов
- •3.4 Каскадный ливень
- •4.1 Процессы поглощения гамма-излучения
- •4.2 Поглощение гамма-излучения.
- •5. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНОВ С ВЕЩЕСТВОМ
- •1. ЯДЕРНЫЕ РЕАКЦИИ С УЧАСТИЕМ НЕЙТРОНОВ
- •1.1 Радиационный захват нейтрона
- •1.2 Реакции с образованием протонов
- •1.4 Реакции деления под действием нейтронов
- •1.6 Неупругое рассеяние нейтронов
- •1.7 Упругое рассеяние нейтронов
- •2. ЯДЕРНЫЕ РЕАКЦИИ С УЧАСТИЕМ ЗАРЯЖЕННЫХ ЧАСТИЦ
- •2.2 Реакции под действием протонов
- •2.3 Ядерные реакции под действием заряженных частиц, ускоренных при высоких энергиях
- •2.4 Ядерные реакции с тяжёлыми ионами
- •2.5 Ядерные реакции с участием электронов, мюонов, мезонов, гиперонов и античастиц
- •3. ФОТОЯДЕРНЫЕ РЕАКЦИИ
- •4. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ
- •1. КЛАССИФИКАЦИЯ ЯДЕРНЫХ РЕАКЦИЙ
- •2. ЗАКОНЫ СОХРАНЕНИЯ В ЯДЕРНЫХ РЕАКЦИЯХ
- •2.1 Барионный заряд
- •2.2 Энергия и импульс
- •2.3 Закон сохранения импульса
- •2.4 Момент количества движения
- •2.5 Чётность
- •2.6 Изотопический спин
- •3. КИНЕТИКА И ВЫХОД ЯДЕРНОЙ РЕАКЦИИ
- •3.1 Сечение ядерной реакции
- •3.2 Скорость ядерной реакции
- •4. МЕХАНИЗМЫ ЯДЕРНЫХ РЕАКЦИЙ
- •4.1 Модель составного ядра
- •4.2 Оптическая модель
- •4.3 Модель прямых механизмов
- •1. ВЫНУЖДЕННОЕ ДЕЛЕНИЕ ЯДЕР
- •1.1 Особенности процесса деления
- •1.2 Жидкокапельная модель ядра в описании деления
- •1.3 Оболочечная модель ядра в интерпретации процесса деления
- •2. ПРОЦЕСС ВЫНУЖДЕННОГО ДЕЛЕНИЯ
- •2.1 Вероятность деления
- •2.2 Стадии процесса деления
- •2.3 Энергетика процесса деления
- •2.4 Продукты деления
- •1. ЦЕПНЫЕ ПРОЦЕССЫ
- •1.1 Цепные реакции в химии
- •1.2 Ядерные цепные реакции
- •1. 3 Цепная реакция деления
- •1.4 Ядерный взрыв
- •1.5 Ядерная безопасность
- •2 КРИТИЧЕСКАЯ МАССА
- •3. ЯДЕРНЫЕ РЕАКЦИИ В АТОМНОЙ БОМБЕ
- •3.1 Урановый заряд
- •3.1.1 Делящиеся изотопы урана
- •3.1.2 Устройство и принцип работы урановой атомной бомбы
- •3.2 Плутониевый заряд
- •4 НЕЙТРОННОЕ ОРУЖИЕ
- •1. ВЗАИМОДЕЙСТВИЯ НЕЙТРОНОВ С ВЕЩЕСТВОМ
- •1.1 Свойства нейтронов
- •1.2 Свойства нейтронов различных энергий
- •1.3 Замедление нейтронов
- •1.4 Замедлители нейтронов
- •1.5 Диффузия нейтронов
- •1.6 Альбедо нейтронов
- •2. НЕЙТРОНЫ В ЯДЕРНОМ РЕАКТОРЕ
- •2.1 Генерация нейтронов
- •2.2 Радиационный захват
- •2.3 Рассеяние нейтронов в реакторе
- •2.4 Основные характеристики нейтронных полей
- •2.5 Размножение нейтронов
- •2.6 Критичность реактора
- •2.7 Распространение нейтронов в среде
- •3. УПРАВЛЕНИЕ ЯДЕРНЫМ РЕАКТОРОМ
- •3.1 Реактивность реактора
- •3.2 Нейтронный цикл
- •3.3 Управление реактором на тепловых нейтронах
- •1. ИСТОРИЯ АТОМИЗМА
- •2. ОБЩАЯ ХАРАКТЕРИСТИКА
- •2.1 Размеры атома
- •2.2 Масса атома
- •2.3 Заряд ядра атома
- •2.4 Внутренняя энергия атома
- •3. ВНУТРЕННЕЕ СТРОЕНИЕ АТОМА
- •3.1 Атом Бора
- •3.2 Теория атома водорода
- •3.3 Квантовомеханическая теория сложных атомов
- •3.4 Электронные оболочки атома и периодическая система элементов
- •4. АТОМНЫЕ ПРОЦЕССЫ
- •4.1 Ионизация
- •4.2 Эмиссия рентгеновского излучения
- •1. РАСПРОСТРАНЕНИЕ ЭЛЕМЕНТОВ И ИЗОТОПОВ
- •2. НАЧАЛЬНЫЙ НУКЛЕОСИНТЕЗ
- •3. ЭВОЛЮЦИЯ ЗВЁЗД
- •4. СКОРОСТЬ ТЕРМОЯДЕРНЫХ РЕАКЦИЙ
- •5. ЗВЁЗДНЫЙ НУКЛЕОСИНТЕЗ
- •5.1 Ядерные реакции в звёздном нуклеосинтезе
- •5.3 Горение гелия
- •5.4 Синтез ядер с А<60
- •5.5 Синтез ядер с А>60
- •5.5.1 s-Процесс
- •5.5.3 р-Процесс
- •6. ПРОБЛЕМА СОЛНЕЧНОГО НЕЙТРИНО
- •6.1 Ожидаемые источники солнечного нейтрино, энергии и потоки
- •6.2 Детектирование нейтрино
- •6.3 Проблема солнечного нейтрино
- •7. СИНТЕЗ Li, Be и B
- •1. ФИЗИЧЕСКИЕ ОСНОВЫ ЯДЕРНОГО СИНТЕЗА
- •1.1 Термодинамика ядерного синтеза
- •1.2 Реакции ядерного синтеза
- •1.3 Термоядерные топлива
- •2. ТЕРМОЯДЕРНЫЙ СИНТЕЗ В ЗЕМНЫХ УСЛОВИЯХ
- •2.1 Водородная бомба
- •2.2 Термоядерный синтез в тепловом урановом реакторе
- •3. УПРАВЛЯЕМЫЙ ТЕРМОЯДЕРНЫЙ СИНТЕЗ
- •3.1 Временные и температурные условия
- •3.2 Магнитное удержание плазмы
- •3.2.1 Плазма
- •3.2.2 Плазма и УТС
- •3.2.3 Системы с замкнутой магнитной конфигурацией
- •3.2.4 Открытые магнитные конфигурации
- •4. УСТАНОВКИ С МАГНИТНЫМ УДЕРЖАНИЕМ
- •4.1 Токамак
- •4.2 Пинч с обращенным полем (ПОП)
- •4.3 Стелларатор
- •4.4 Открытая ловушка
- •4.5 Плазменный фокус
- •4.6 Галатея
- •5. УСТАНОВКИ ИНЕРЦИОННОГО СИНТЕЗА
- •6. ВОДОРОДНАЯ БОМБА
- •1. АКТИВАЦИОННЫЙ АНАЛИЗ
- •1.1 Основы метода
- •1.2 Практика нейтронно-активационного анализа
- •1.2.2 Анализ наведённой активности
- •1.3 Применения активационного анализа.
- •1.4 Преимущества и недостатки активационного анализа
- •2. РЕНТГЕНОВСКИЙ ЭМИССИОННЫЙ АНАЛИЗ
- •3. РЕЗЕРФОРДОВСКОЕ ОБРАТНОЕ РАССЕЯНИЕ
- •1. ОСОБЕННОСТИ КВАНТОВОЙ МЕХАНИКИ
- •2. КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ
- •3. ПРИНЦИП НЕОПРЕДЕЛЁННОСТИ ГЕЙЗЕНБЕРГА
- •4. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ
- •4.1 Уравнение Шрёдингера
- •4.2 Волновая функция
- •4.3 Потенциальная яма
- •5. ПРИНЦИП ПАУЛИ
- •6. РАСПРЕДЕЛЕНИЯ
- •6.1 Распределение Максвелла-Больцмана
- •6.2 Распределение Бозе-Эйнштейна
- •6.3 Распределение Ферми-Дирака
- •1. АТОМНОЕ ЯДРО – общие сведения
- •2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДРА
- •2.1 Открытие ядра
- •2.2 Заряд атомного ядра
- •2.3 Масса атомного ядра
- •2.4 Размеры ядра и распределение плотности ядерной материи
- •2.5 Спин и магнитный момент ядра
- •Как и составляющие его нуклоны, ядро имеет собственные моменты: спин, магнитный момент и электрический квадрупольный момент.
- •2.6 Энергия связи и устойчивость ядер
- •2.7 Электрический момент ядра
- •2.8 Чётность
- •2.9 Изоспин нуклонов и ядер
- •3. ЯДЕРНЫЕ СИЛЫ
- •1. МОДЕЛИ СТРОЕНИЯ АТОМНОГО ЯДРА
- •1.1 Классификация моделей
- •1.2 История развития моделей ядра
- •2. КАПЕЛЬНАЯ МОДЕЛЬ СТРОЕНИЯ ЯДРА
- •3. ОБОЛОЧЕЧНАЯ МОДЕЛЬ ЯДРА
- •3.1 Экспериментальное обоснование оболочечной модели
- •3.2 Построение оболочечной модели
- •3.3 Ядерные потенциалы и энергетические уровни ядра
- •3.4 Систематика энергетических уровней
- •3.5 Следствия оболочечной модели
- •1. ЧАСТИЦЫ
- •2. КЛАССИФИКАЦИЯ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- •3. СВОЙСТВА НЕКОТОРЫХ ФУНДАМЕНТАЛЬНЫХ ЧАСТИЦ
- •3.1 Фотон
- •3.2 Протон
- •3.3 Нейтрон
- •3.4 Нейтрино
- •4. КВАРКИ
- •5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТИЯ
- •5.1 Виды взаимодействий
- •5.2 Сильные взаимодействия
- •5.3 Квантовая хромодинамика
- •6. АНТИМАТЕРИЯ
- •1. РАДИОАКТИВНОСТЬ
- •2. ИСТОРИЧЕСКАЯ СПРАВКА
- •3. СТАТИСТИКА РАСПАДА
- •4. ЗАКОНЫ СОХРАНЕНИЯ В РАСПАДАХ
- •5.1 Долина ядерной стабильности
- •5.2 Новые тяжёлые элементы
- •5.3 «Доводородные» элементы
- •5.4 «Экзотические» ядра
- •5.5 На пути к нейтронной материи
- •1. РАДИОАКТИВНЫЙ РАСПАД И ИОНИЗИРУЮЩИЕ ИЗЛУЧЕНИЯ
- •2. ОСНОВНЫЕ ТИПЫ ЯДЕРНЫХ ПРЕВРАЩЕНИЙ
- •2.1 Альфа-распад
- •2.1.1 Основные особенности
- •2.2 Бета - распад
- •2.2.3 Электронный захват
- •2.3.1 Внутренняя конверсия электронов
- •2.3.2 Ядерная изомерия
- •1. КЛАССИФИКАЦИЯ ПРОЦЕССОВ РАСПАДА
- •2. СПОНТАННОЕ ДЕЛЕНИЕ
- •2.1 Самопроизвольное деление тяжёлых ядер
- •2.2 Механизм деления
- •2.3 Энергетика спонтанного деления
- •2.4 Продукты деления
- •2.5 Спонтанное деление из изомерного состояния
- •3. ПРОТОННАЯ РАДИОАКТИВНОСТЬ
- •4. НЕЙТРОННАЯ РАДИОАКТИВНОСТЬ
- •7. ЗАПАЗДЫВАЮЩЕЕ ДЕЛЕНИЕ
- •8. КЛАСТЕРНАЯ РАДИОАКТИВНОСТЬ
- •9. БЕТА-РАСПАД ПОЛНОСТЬЮ ИОНИЗИРОВАННОГО АТОМА
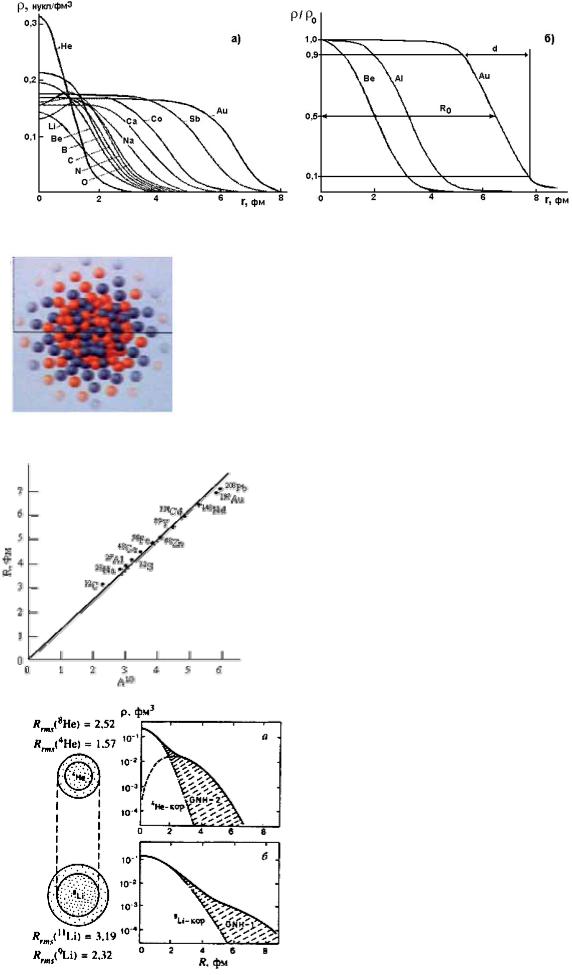
ожидать, что протоны вытесняются наружу протонным отталкиванием, а нейтроны смещаются во внутреннюю область ядра.
Плотность ядерной материи в центре ядра ρ0 приблизительно одинакова у всех ядер и составляет ~0.17 нукл./фм3 (Рис. 9). Толщина поверхностного слоя у всех ядер тоже примерно одинакова и равна 2.4 фм.
Рис. 9. Плотность распределения ядерной материи в ядрах различных элементов: а) исходный масштаб, б) Нормировка на типичную плотность.
Рис. 10. Схема распределения нуклонов по объёму ядра.
Атомные ядра вблизи долины стабильности (см. далее) представляют собой довольно компактные объекты. Их радиусы меняются от 2-3 фм для самых легких ядер до 7-8 фм для самых тяжелых. Однако для ядер, удаленных от долины стабильности, ситуация иная. Для некоторых ядер, перегруженных нейтронами (протонами), наблюдается так называемый нейтронный (протонный) слой - область вблизи поверхности ядра, в которой с учётом фактора нормировки N/Z ρn>ρp (ρp>ρn).
Влегких ядрах с большим отношением N/Z было открыто нейтронное гало. Оно наблюдается в ядрах,
укоторых энергия связи нейтрона Bn<1-1.5МэВ. В гало-ядрах наряду с приповерхностным слоем (кором), для
которого плотность распределения протонов и нейтронов совпадают, существует довольно большая область на периферии ядра, в которой плотность распределения нейтронов ρn существенно больше плотности распределения протонов ρp(ρn>>ρp). Обнаружены также ядра, имеющие протонное гало.
Рис.11. Радиусы ядер, полученные в экспериментах по рассеянию электронов.
Нейтронное облако, окружающее кор (внешнюю оболочку) ядра, простирается на гораздо большие расстояния, чем радиус ядра, определяемый соотношением R=1.3A1/3. Так для гало-ядра 11Li пространственное распределение двух нейтронов, образующих ядерное гало вокруг кора 9Li, простирается столь далеко, что радиус ядра
11Li оказывается сравним с радиусом ядра 208Pb.
Рис. 12. Распределение нейтронной плотности в гало-ядрах
2.5 Спин и магнитный момент ядра
Как и составляющие его нуклоны, ядро имеет собственные моменты: спин, магнитный момент и электрический квадрупольный момент.
Представление о спине и магнитном моменте ядра было введено для объяснения сверхтонкой структуры спектральных линий.
Спин (англ. Spin, букв. – вращение), собственный момент количества движения микрочастицы, имеющий квантовую природу и не связанный с

движением частицы как целого; измеряется в единицах постоянной планка ћ и может быть целым (0, 1, 2,…) или полуцелым (1/2, 3/2,…).
Ядро, как пространственно ограниченная и связанная система взаимодействующих между собой нуклонов, может рассматриваться в целом как одна микрочастица. Поскольку нуклоны обладают собственным механическим моментом, или спином, равным ħ/2, то и ядра должны иметь механические моменты. Кроме того, нуклоны совершают движение относительно друг друга (орбитальное движение относительно центра движения ядра), которое также характеризуется определённым моментом количества движения каждого нуклона. Орбитальные моменты принимают только целочисленные значения ħ (постоянная Дирака). По этим причинам ядра должны иметь собственный механический момент или спин. Все механические моменты нуклонов, как спины, так и орбитальные, суммируются алгебраически и составляют спин ядра.
Несмотря на то, что число нуклонов в ядре может быть очень велико, спины ядер обычно невелики и составляют не более нескольких ħ, что объясняется особенностью взаимодействия одноимённых нуклонов. Все парные протоны и нейтроны взаимодействуют только так, что их спины взаимно компенсируются, то есть пары всегда взаимодействуют с антипараллельными спинами. Суммарный орбитальный момент пары также всегда равен нулю. В результате ядра, состоящие из чётного числа протонов и чётного числа нейтронов, не имеют механического момента. Отличные от нуля спины существуют только у ядер, имеющих
всвоём составе непарные нуклоны, спин такого нуклона суммируется с его же орбитальным моментом и имеет какое-либо полуцелое значение: 1/2, 3/2, 5/2. Ядра нечётно-нечётного состава имеют целочисленные
спины: 1, 2, 3 и т. д. (У протона и нейтрона спин одинаков и равен ½, поэтому все ядра с четным А имеют целый спин, а ядра с нечетным А – полуцелый спин).
Два нейтрона с одинаковой энергией и одинаковыми (нулевыми) значениями орбитального момента должны иметь разные значения проекции спина на выделенную ось, т.е. +1/2 и -1/2. Сумма спинов нейтронов
вэтом случае равна 0. Эта же ситуация реализуется для двух протонов. Поэтому суммарный момент такой четверки нуклонов - т.е. ядра 4 Не - равен 0.
Спин ядра I есть векторная сумма полных моментов Jk |
отдельных нуклонов, каждый из которых |
||||
складывается из орбитального момента lrk |
и спина нуклона sk , так что |
|
|||
r |
A r |
r |
r |
r |
(9) |
I = ∑Jk ; |
Jk |
= lk + sk . |
|||
k=1
Возможна другая схема сложения моментов отдельных нуклонов, когда сначала по отдельности суммируются векторы спинов и векторы орбитальных моментов всех нуклонов, затем полученные два вектора складываются. Однако, поскольку ядерные силы не центральны и в ядре существует спинорбитальное взаимодействие, то по этой причине в теории ядра используют первую схему.
Естественной единицей измерения момента импульса в квантовой механике служит постоянная Планка ħ = 1,0546·10-34Дж·с, имеющая размерность момента импульса.
Вектор момента любых микрочастиц, как, впрочем, и спина ядра, обладает своеобразными свойствами.
Абсолютная величина вектора момента любой изолированной физической величины может принимать только дискретные значения:
|
|
I |
|
= h I (I +1) |
(10) |
|
|
|
|||
где I – либо целое, либо полуцелое положительное число: |
|
||||
Число I называют |
I = 0, 1/2, 1, 3/2, ... |
(11) |
|||
обычно величиной момента или квантовым числом момента. Следует особо |
|||||
отметить различие между |
модулем вектора I и квантовым числом I, так как последнее является одним из |
||||
чисел (11), используемых в формуле (10) для нахождения модуля вектора I . Когда говорят: «момент 1/2», то имеют в виду именно это квантовое число в формуле (10). В формуле (9) квантовое число lk для орбитального момента всегда целое число, lk = 0, 1, 2, … , а нуклоны (и электрон тоже) имеют квантовое число спина s = 1/2 (спин равен 1/2).
Мгновенное значение вектора любого механического момента не имеет смысла по той же причине, по которой в квантовой механике не имеет смысла мгновенное значение вектора импульса. Строго фиксированное значение может иметь только абсолютная величина вектора момента (10) и одна из его пространственных проекций, обычно называемой проекцией на ось Z, которая обозначается как Iz. Проекция момента Iz может принимать случайным образом одно из (2I + 1) значений, уменьшающихся на единицу:
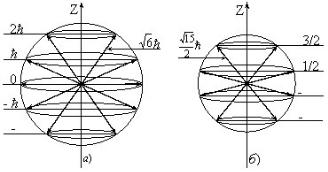
Iz = Iћ, (I– 1)ћ, . . . , -Iћ. |
(12) |
Реализация любой возможной проекции из набора (12) оказывается равновероятной.
Рис. 13. Пространственная модель вектора механического момента.
Число возможных проекций на ось Z четно, если I – полуцелое число, и нечетно, если I – целое число. Знак плюс или минус в (11) означает ориентацию вектора момента на выбранное направление оси Z в пространстве. Однако величины проекций Ix и Iy не имеют определенных значений и флуктуируют относительно нулевого среднего значения. Учитывая, что
I 2 |
= Ix2 +I 2y+Iz2 |
(13) |
имеем |
|
|
Ix2 + I y2 |
= I 2 − Iz2 = I |
(14) |
Таким образом, квадраты проекций вектора момента на оси Х и Y не равны нулю. По этой причине проекция момента Iz всегда меньше абсолютной величины вектора механического момента. Максимальное значение
(Iz2 )max = (Ih)2 ,тогда
I 2 = h2 I (I +1)= (Ih)2 + Ih2 |
(15) |
Все перечисленные выше свойства вектора механического момента обычно демонстрируют с помощью квазиклассической модели, которая находится в определенном согласии со свойствами квантовомеханического вектора момента. Вектор момента прецессирует относительно оси Z с некоторой угловой скоростью и может ориентироваться вдоль или против направления оси Z только таким образом, чтобы его проекция на ось Z была равна одному из значений от +Iћ до –Iћ через единицу. Этот вектор никогда не может ориентироваться точно по направлению оси Z, поскольку его модуль, как отмечено выше, не равен Iћ. Поэтому, помимо его модуля, сохраняющейся во времени величиной является только одна проекция вектора – проекция на ось Z. Полное число проекций Iz вектора момента равно (2I + 1).
Модуль вектора момента Ir3 сложной системы, составленной из двух взаимодействующих систем с
моментами I1 и I2 , вычисляется из выражения
Ir32 = (Ir1 + Ir2 )2 = I3 (I3 +1)h2 (16)
обычным образом через свои квантовые числа I3. Сложение векторов I1 и I2 есть сложение их проекций как алгебраических чисел. Для получения возможных проекций вектора I3 каждая из проекций вектора I1 складывается с одной из соответствующих проекций вектора I2 . Таких проекций оказывается всего (2I1 + 1)(2I2 + 1), которые будут образовывать (2Im + 1) векторов I3 , Im = min{I1,I2}, со следующими значениями квантовых чисел:
I3 = I1 + I2 , I1 + I2 −1,..., |
|
I1 − I2 |
|
. |
(17) |
|
|
Соотношение (17) называется правилом сложения моментов в квантовой механике.
Поскольку каждое значение проекции из (2I1+1)(2I2+1) возможных реализуется с равной вероятностью, то относительная вероятность образования состояния со спином I´ из возможного набора значений (17) составит
g = |
|
2I '+1 |
(18) |
|
(2I1 +1)(2I2 +1) |
|
|||
т.е. равна отношению числа возможных проекций |
вектора I ' |
к полному числу проекций возможных |
||
значений вектора Ir3 . Величина g называется статистическим фактором или статистическим весом. |
||||
Любая векторная величина A , характеризующая |
физические свойства микрочастицы, |
|||
пропорциональна вектору момента I : |
|
|
|
|
A = aI |
(19) |
|
||
где а – константа, полностью характеризующая вектор.

Вотношении спинов различных ядер наблюдаются следующие опытные закономерности: а) Для ядер с четными А спины всегда целые, а при нечетном А – всегда полуцелые.
б) Чётно-чётные ядра (А – чётное) в основном состоянии имеют спин равный нулю. Этот факт дает основания считать, что одноименные нуклоны объединяются в пары (эффект спаривания) с противоположно направленными спинами, так что суммарный момент импульса оказывается равным нулю.
в) Нёчетно-нёчетные ядра (А - чётное) имеют целочисленный спин. Это указывает на то, что разноименные нуклоны объединяются в пары с одинаковым направлением спинов, создавая единичный момент.
г) Ядра с нёчетным А имеют полуцелый спин в пределах от 1/2 до 9/2, что свидетельствует о том, что спины и орбитальные моменты большинства нуклонов компенсируются и не участвуют в создании спина ядра
Магнитный момент – основная физическая величина, характеризующая магнитные свойства вещества. Магнитными моментами обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитные моменты отдельных элементарных частиц (электронов, протонов, нейтронов) обусловлено существованием у них спина. Магнитные моменты ядер складываются из спиновых магнитных моментов протонов и нейтронов, образующих эти ядра, а также из магнитных моментов, связанных с их орбитальным движением внутри ядра по тем же правилам, по которым вычисляется спин ядра.
Магнитный момент - векторная величина, характеризующая вещество как источник магнитного поля. Макроскопический магнитный момент создают замкнутые электрические токи и упорядоченно ориентированные магнитные моменты атомных частиц (например, у электронов в атомах) и спиновые, связанные со спином частицы. Магнитный момент тела определяется векторной суммой частиц, из которых тело состоит.
Магнитный дипольный момент частицы является оператором в пространстве волновых функций частиц и связан с операторами орбитального и спинового моментов. Значение магнитного дипольного момента электрона, протона и нейтрона в системах координат, связанных с каждой из частиц, в магнетонах равно половине гиромагнитного отношения gs.
Всоответствии с (19) магнитный момент ядра равен
μr = gI |
(20) |
где g – гиромагнитный множитель (отношение), равный отношению величины магнитного момента к величине механического:
|
|
|
r |
|
|
|
|
|
|
g = |
|
|
μr |
|
|
= |
e |
μ |
(21) |
|
|
||||||||
|
|
|
|
2mpc |
|||||
|
|
|
I |
|
|
|
|
||
В (21) приняты следующие обозначения: е– элементарный электрический заряд; mp – масса протона; с – скорость света в вакууме; μ – безразмерное число.
Таким образом, значение магнитного момента ядра (в ядерных магнетонах) пропорционально значению спина ядра. Проекция магнитного момента μ на ось Z, которая совпадает с направлением
внешнего магнитного поля, равна:
|
μH = ghIH = |
eh |
μI = μB μI, |
(22) |
|||
|
2mpc |
||||||
|
|
|
|
|
|
||
где величина |
eh |
|
|
|
|
|
|
μB = |
= 5,0508343 10−27 |
Дж Тл−1 |
(23) |
||||
2mpc |
|||||||
|
|
|
|
|
|
||
называется ядерным магнетоном Бора. Ядерный магнетон Бора в mp/me=1836 раз меньше электронного магнетона Бора, используемого в атомной физике.
Магнитный момент ядра равен целому кратному ядерного магнетона Бора.
Те́сла (русское обозначение: Тл; международное обозначение: T) - единица измерения индукции магнитного поля в СИ, численно равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон.
Магнетон Бора является такой же универсальной единицей измерения магнитных моментов ядер, какой служит элементарный электрический заряд е для измерения заряда тел, или постоянная планка ħ для измерения механических моментов. Точно так же безразмерное число μ служит для измерения магнитных моментов ядер в единицах ядерных магнетонов Бора μВ, подобно атомному номеру Z при измерении заряда ядер в единицах е, или квантовым числам при измерении механических моментов в единицах постоянной Планка ħ.
Магнитный момент нейтрона μn=-1,91μB (направлен противоположно спину), протона +2,79μB (момент направлен по спину). Отличие магнитного момента протона от одного ядерного магнетона является удивительным результатом. Еще более удивительным представляется существование магнитного момента у

не имеющего заряда нейтрона. Эти факты до сих пор не объяснены: они указывают на сложную структуру нуклонов.
Рассмотрим квантовое число спина.
1.Jе > I. По правилу сложения моментов, квантовое число полного момента F может принимать (2I + 1) значений, чем и будет определяться число линий сверхтонкого расщепления. Подсчитав это число и приравняв его числу (2I + 1) непосредственно находим спин ядра (квантовое число спина).
2.1 > Jе. В этом случае, если линий сверхтонкого расщепления больше двух, применяют правило интервалов. Находим величину интервала U12, т.е. разность значений энергии U1 и U2, которые определяются для двух соседних значений F и F-1 при фиксированных величинах Jе и I:
|
|
|
|
|
|
|
gah2 |
|
|||||
|
|
U12 = |
|
|
|
|
F, |
(24) |
|||||
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
а затем величину интервала U23,отвечающую двум соседним значениям F-1 и F-2: |
|||||||||||||
|
|
U23 |
= |
gah2 |
(F −1) |
(25) |
|||||||
|
|
|
|
|
|||||||||
Отношение соседних интервалов U12 и |
U23 |
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
U12 |
= |
|
F |
|
= |
|
|
I + Je |
|
(26) |
||
|
U23 |
F −1 |
|
I + Je +1 |
|||||||||
|
|
|
|
|
|||||||||
По измеренному отношению U1/ U2 и Jе, определяется квантовое число I спина ядра. Если компонент сверхтонкой структуры всего две и правило интервалов применить нельзя (интервал всего один), то спин ядра можно оценить по отношению интенсивностей компонент, каждая из которых определяется своим статистическим весом. Спин ядра можно также определить по расщеплению спектральных линий (эффект Зеемана) в магнитном поле, создаваемым внешним макроскопическим током, например, катушкой с током.
Особенно точным методом определения магнитных моментов ядер является метод ядерного магнитного резонанса (ЯМР).
Табл.1. Спины и магнитные моменты некоторых ядер
Ядро |
Спин I в ћ |
μ в μВ |
Ядро |
Спин I в ћ |
μ в μВ |
n |
½ |
-1,91 |
6C12 |
0 |
0 |
p |
½ |
+2,79 |
6C13 |
½ |
+0,7 |
1H2 |
1 |
0,86 |
7N14 |
1 |
+0,4 |
1H3 |
½ |
+3 |
7N15 |
½ |
-0,28 |
2He3 |
½ |
-2,1 |
8O16 |
0 |
0 |
2He4 |
0 |
0 |
8O17 |
5/2 |
-1,0 |
3Li6 |
1 |
+0,8 |
49In115 |
9/2 |
+5,5 |
3Li7 |
3/2 |
+3,2 |
83Bi209 |
9/2 |
+4 |
4Be9 |
3/2 |
-1,2 |
82Pb208 |
0 |
0 |
5B10 |
3 |
+1,8 |
92U235 |
7/2 |
-0,35 |
|
|
|
94Pu239 |
1/2 |
+0,2 |
В Табл. 1. приведены спины I и приближенные значения магнитных моментов μ для нуклонов и некоторых легких, средних и тяжелых ядер. Знак минус у магнитного момента указывает на то, что он направлен противоположно спину. Ядра, имеющие нулевой спин, обладают нулевым магнитным моментом.
Измерения спинов стали возможными благодаря наличию непосредственно связанных с ними магнитных моментов. Они измеряются в магнетонах и у различных ядер равны от −2 до +5 ядерных магнетонов. Из-за относительно большой массы нуклонов магнитные моменты ядер очень малы по сравнению с магнитными моментами электронов, поэтому их измерение гораздо сложнее. Магнитный момент чётно-чётных пар, как и спин, равен нулю. Магнитные моменты ядер с непарными нуклонами образуются собственными моментами этих нуклонов и моментом, связанным с орбитальным движением непарного протона
Нейтроны и протоны в ядре располагаются таким образом, что их спины и магнитные моменты взаимно компенсируются (в чётно-чётных ядрах наблюдается полная компенсация). Максимальный спин ядра не превышает нескольких единиц, т.е. он гораздо меньше А/2, чему он должен был бы равняться, если бы спины всех нуклонов складывались. Также обстоит дело и с магнитными моментами. (Тот факт, что магнитный момент ядер не превышает несколько ядерных магнетонов, служит свидетельством против протонно-электронной модели ядра. Если бы в состав ядра входили электроны, то магнитные моменты ядер
