
- •Лекция 14
- •6.2. Процессы, контролируемые изменением поверхностной энергии
- •Образование граней на кристаллах
- •Рост частиц второй фазы
- •Изменение химического потенциала частиц второй фазы
- •Изменение химического потенциала частиц второй фазы
- •Форма растущих выделений
- •Форма растущих выделений
- •Рост выделений происходит в объеме зерна
- •Рост выделений в объеме зерна
- •Рост выделений происходит в объеме зерна твердого тела
- •Рост выделений, контролируемый переносом атомов через межфазную границу
- •Рост выделений, контролируемый переносом атомов через межфазную границу (продолжение)
- •Рост выделений, контролируемый переносом атомов через межфазную границу (продолжение)
- •Рост выделений, контролируемый переносом атомов через межфазную
- •Рост выделений на межзеренных границах
- •Рост выделений на межзеренных границах
- •Рост выделений на малоугловых границах
- •Временные зависимости роста второй фазы (итог)
- •Результаты исследования роста выделений
- •Результаты исследования роста выделений
- •Меры по управлению ростом выделений
- •Меры по управлению ростом выделений
- •Меры по управлению ростом выделений
- •Меры по управлению ростом выделений
- •Меры по управлению ростом выделений
- •Общие выводы о росте выделений
- •6.3. Стабильность волокнистых и пластинчатых структур
- •6.3. Стабильность волокнистых структур
- •6.3. Стабильность пластинчатых структур
- •6.3. Стабильность пластинчатых структур
- •6.4. Изменение микроструктуры под влиянием энергии межзеренных границ
- •Нормальный рост зерна
- •Нормальный рост зерна
- •Нормальный рост зерна (продолжение)
- •Нормальный рост зерна (продолжение)
- •Нормальный рост зерна (продолжение)
- •Аномальный рост зерна
- •Аномальный рост зерна
- •Аномальный рост зерна
- •7. Другие внешние причины нестабильности структурно-фазового состояния
- •Движение включений в твердых телах
- •Движение включений в твердых телах за счет диффузионных потоков вакансий (продолжение)
- •2.Механизм поверхностной диффузии, вызывающий движение включений
- •3.Механизм движения включений в твердых телах связан с переносом атомов матрицы через само
Лекция 14
Модуль 3. Структура и ее роль в обеспечении заданного комплекса свойств материалов.
Тема 3.4. Стабилизация структурно-фазового состояния материалов
(продолжение)
6.2. Процессы, контролируемые изменением поверхностной энергии
Избыточная свободная поверхностная энергия стимулирует протекание ряда процессов, идущих при Gпов min.
При Gпов = dA изменения могут быть связаны или с
изменением уровня поверхностной энергии min, или с сокращением площади поверхности А min. Кроме этого,
будем помнить, что избыток свободной поверхностной энергии определяет избыток химического(потенциалаG / С)T , V :
=
значение которого при равновесии системы = 0.
Рассмотрим следующие процессы, контролируемые Gпов min:
-образование граней на кристаллах; -рост частиц второй фазы;
-рост выделений второй фазы в разных местах с труктуры; -стабильность волокнистых и пластинчатых структур;
-изменение |
микроструктуры |
под |
влиянием |
энергии |
межзеренных границ.
Образование граней на кристаллах
При наличии шероховатости поверхности общая поверхностная энергия будет складываться из множества слагаемых, соответствующих участкам поверхности:
Gпов = dA
При нагревании такой поверхности с течением времени сохраняются плоскости с наиболее плотной упаковкой атомов как обладающие минимальными площадями поверхности и, следовательно, поверхностной энергии.
Под действием Gпов min. происходит огранение
кристалла с сохранением наиболее плотноупакованных плоскостей (плоскостей с малыми индексами типа 111 ).
Элементарными физическими механизмами огранения кристаллов являются диффузия и сублимация (испарение) атомов.
В результате, если кристалл мал, то образуется многогранник, а с ростом времени дальнейшее сокращение площади поверхности может привести к образованию сферы, обладающей минимальной площадью поверхности
из известных геометрических фигур.
Рост частиц второй фазы
Дисперсные частицы фазы обладают высоким суммарным уровнем поверхностной энергии межфазных границ и в совокупности дают высокий избыток свободной поверхностной энергии.
При нагревании такая система будет стремиться сократить площадь поверхности, например, за счет растворения мелких и укрупнения крупных частиц, так как при этом наиболее эффективно сокращается площадь поверхностей межфазных границ.
Такой процесс известен как рост частиц по механизму
Оствальда – коалесценция по Оствальду.
Уровни удельной свободной энергии поверхности раздела выделений:
-когерентные выделения Ni3Al в никеле - 0,02 Дж/м2 ;
-границы зерен - до 0,6 Дж/м2 ;
-некогерентные частицы оксида, например Th2O в никеле - до
1,5 Дж/м2.
Величина избытка энергии сплава, например, в системе Cu–Co: когерентные выделения на расстоянии = 30 нм друг
от друга, плотность1022 м–3, а площадь поверхности А = 107 м2/м3, при 0,2
Дж/м2, то получим суммарное значение свободной
Изменение химического потенциала частиц второй фазы
|
В |
эвтектической |
системе |
||||||
|
возможно |
|
выделение |
||||||
|
плоских (r = ) и |
||||||||
|
сферических (r ) частиц. |
|
|||||||
|
|
Изменение |
|
|
|
|
|||
|
равновесной |
|
|
вызвано |
|||||
|
растворимости |
|
|||||||
|
увеличением |
химического |
|||||||
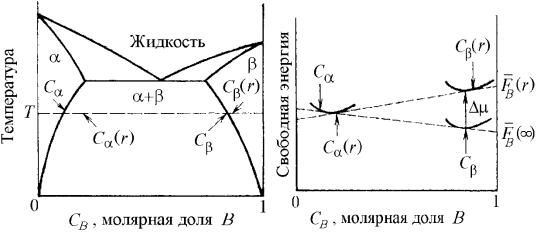
Типичная фазовая диаграмма (а) и график |
потенциала выделившейся |
||||||||
зависимости свободной энергии F(r) от |
фазы . |
|
|
|
малого |
||||
состава (б): линия С –С соответствует |
При |
переходе |
|
||||||
равновесию плоских (r = ) выделений - |
количества |
фазы |
(dn |
||||||
фазы; линия С (r)–С (r) соответствует |
молей) |
состава |
С |
|
из |
||||
равновесию выделений -фазы конечного |
выделения |
с |
|
плоской |
|||||
размера r. |
границей раздела (r = ) к |
||||||||
Такой переход вызывает увеличение свободной энергии dG |
= |
||||||||
dF = dn = dA, |
выделению |
радиусом |
r |
||||||
|
имеет |
место |
|
считаюприрост |
|||||
где А – площадь поверхности выделения, а |
|
||||||||
изотропной. |
химического |
|
потенциала |
||||||
Следовательно, = dA/dn. Известно, что А |
= |
4 r , |
|||||||
|
. |
|
|
|
|
|
|
|
2 |
поэтому dA/dr = 8 r. Число молей |
выделений n |
в |
сфере |
||||||
радиуса r равно n = 4 r3/(3Vм), поэтому
dn/dr = 4 r2/Vм, где Vм – молярный объем выделений, т.е. объем,
Изменение химического потенциала частиц второй фазы
(продолжение)
= 2 Vм/r
Комментарий к уравнению:
-множитель 2/r - кривизна поверхности = (1/ r1 + 1/r2) для несферических поверхностей, где r1 и r2 – два
перпендикулярных радиуса кривизны несферической поверхности; -при переходе плоского выделения в выделение с кривизной (r):
-увеличивается свободная энергия на , изменяя
парциальную молярную свободную энергию (FB);
- увеличивается растворимость компонента В в -фазе,
С (r).
-чем меньше радиус частицы второй фазы, тем выше уровень свободной энергии и больше движущая сила растворения такого выделения.
-для любых выделений радиусом в несколько нанометров существует следующее соотношение растворимости компонента В в -фазе:
С (r) = C ( ) (1 + 2 Vм /R T r)
где C ( ) – растворимость В в -фазе при плоском выделении.
При растворении мелких выделений и одновременном
Форма растущих выделений
Роль упругих напряжений проявляется в том, что равновесные формы выделений могут иметь различные формы, при которых упругие напряжения минимальны:
-в системе Cu–Fe равновесной формой выделений является стержень с отношением d/l = ¼, в этом случае имеет место кристаллографическое совпадение плоскостей выделения и матрицы, например, ось медного выделения параллельна направлению плотной упаковки <110> ГЦК- атомов и <111> в ОЦК-матрице железа, т.е.:
Cu<110>(ГЦК)|| -Fe<111>(ОЦК)
Отношение диаметр/длина стерженьковых выделений равно 1/4, что указывает на низкие значения для поверхностей, в которых лежит
направление плотной упаковки.
Форма растущих выделений
(продолжение)
-в системе Al–Cu равновесной формой выделений могут быть диски с отношением
d/h = 25/1;
-в системе Cu–Co равновесной формой выделений могут быть сферические выделения.
Обнаружено, что в течение всего времени роста форма выделений остается неизменной, что свидетельствует о равновесности формы выделений.
Стабильная форма растущих частиц определяется соотношением поверхностной и упругой энергий в решетке системы. Это означает,
что кинетика роста частиц второй фазы под действием избытка
свободной поверхностной энергии весьма чувствительна к структуре
среды, в которой идет рост.
Рассмотрим кинетику роста выделений в зерне, на большеугловых и малоугловых границах зерен
Рост выделений происходит в объеме зерна
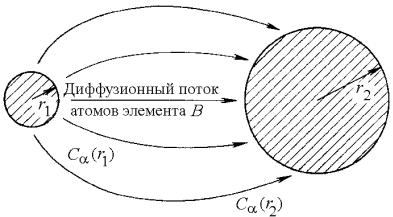
В этом случае рост выделений контролируется объемной диффузией. Концентрация растворенного в матрице вещества возле каждого выделения будет соответствовать его равновесной растворимости. Но это означает, что количество растворенного вещества, находящегося в равновесии с выделением,
1 – С (r1), будет больше, чем с выделением 2 – С (r2), так как поверхность
выделения 1 меньше выделения 2.
Поэтому возникнет диффузионный поток атомов В в направлении от 1 к 2, как это показано на рис.
По мере того, как r1 будет уменьшаться, а С (r1) – возрастать,
процесс будет развиваться с возрастающей скоростью до тех пор, пока не произойдет исчезновения малого выделения и система не останется с относительно большим выделением.
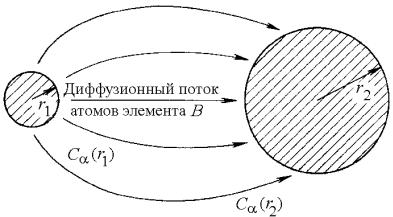
Рост выделений в объеме зерна
(продолжение)
Диффузионный поток (моль/с) к
растущему выделению на расстоянии R от него равен – 4 R2D (dC1/dR ).
Здесь: С1 – концентрация, равная числу атомов в единице объема, т.е. молярная концентрация
С, деленная на молярный объем Vм:
С1 = С/Vм.
В таком случае поток атомов:
= – 4 R2D (dC1/dR ) 1/Vм.
Именно этот поток обусловливает скорость роста выделения . Если учесть, что:
1/r D С ( ) – С (r) , где C ( ) – равновесная концентрация
твердого раствора с выделением среднего размера rc;
объем выделения V = (4/3) r3 ;
число молей внутри выделения n = V/Vм = 4 r3/3Vм,
то после интегрирования и преобразований получим для скорости роста уравнение
dR/dt = 2D VмC ( ) (1/rc–1/r)/RTr.
